Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Angles at Centre & Semicircles
Angles at Centre & Semicircles | Mathematics for GCSE/IGCSE - Class 10 PDF Download
What are circle theorems?
- You will have encountered various angle facts, such as those in polygons and parallel lines. Circle Theorems focus on angle properties that arise when lines are drawn within and connected to a circle.
- Circle Theorems involve understanding angle relationships that occur within circles and in connection with circle components.
What do I need to know about Circle Theorems?
- To master Circle Theorems, you should be able to identify and understand the roles of circle elements like radius, diameter, arc, sector, chord, segment, and tangent.
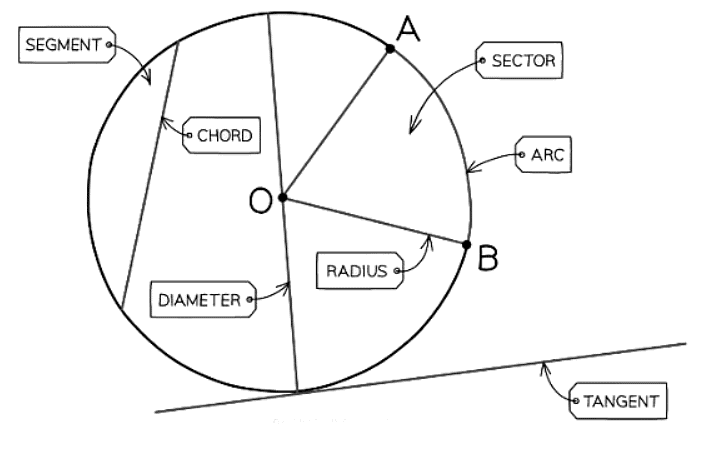
- Solving certain problems may require using known angle facts from triangles, polygons, and parallel lines.
- You might also need to use the formulas for circumference and area, so make sure you know them:
- Circumference = π × diameter (C = πd)
- Area = π × radius squared (A = πr2)
Angles at Centre & Circumference
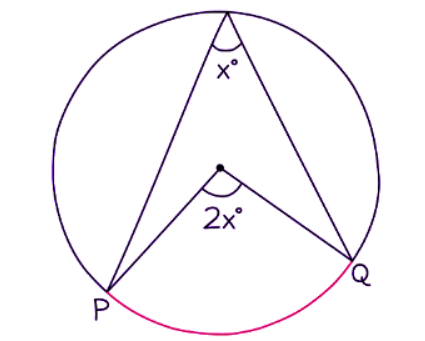
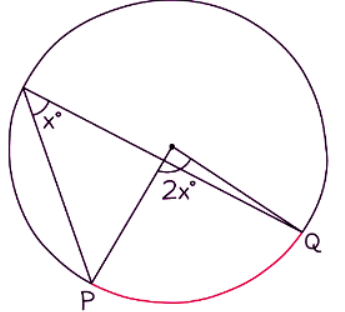
Circle Theorem: When considering a circle, the angle subtended by an arc at the center is precisely twice the angle formed at the circumference.
- This particular theorem holds significant value within the realm of circle theorems and acts as a foundational concept for various other angle-related facts within circles.
- In this theorem, both the chords (radii) extending to the center and those reaching out to the circumference originate from the endpoints of the same arc.
- It's relatively simple to identify this theorem within a diagram. Here's how you can do it:
- Identify any two radii within the circle and trace them out to the circumference.
- Observe if there are lines extending from these points to any other point on the circumference.
- When applying this theorem, especially in an exam setting, it's crucial to emphasize the phrase: "The angle at the center is twice the angle at the circumference."
- This fundamental theorem essentially states that the angle formed at the center of a circle is twice as large as the angle created at the circumference.
- When parts of triangles overlap, a theorem can still apply.
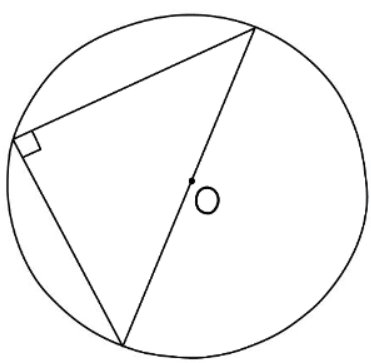
Circle Theorem: The angle in a semicircle is always a right angle.
- This rule is a specific case of the angle at the center theorem.
- The angle on the diameter measures 180°, while the angle at the circumference is 90°.
- To identify this, locate a diameter within the circle and ensure it passes through the center.
- Questions often present only half of a circle, appearing in either whole circles or semicircles.
- Any angle at the circumference originating from the diameter's ends will always be 90°.
- Commonly referred to as the angle in a semicircle theorem, it's crucial to use the specific keywords during exams.
- Watch out for triangles camouflaged among other shapes within the circle.
The document Angles at Centre & Semicircles | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
109 videos|689 docs|60 tests
|
FAQs on Angles at Centre & Semicircles - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the relationship between angles at the centre of a circle and semicircles? |  |
Ans. Angles at the centre of a circle are twice the size of angles at the circumference. In a semicircle, the angle at the centre is always 90 degrees.
| 2. How can angles at the centre of a circle help us find missing angles in geometry problems? |  |
Ans. Angles at the centre of a circle can be used to find missing angles by applying the rule that angles at the centre are twice the size of angles at the circumference. This can help solve geometry problems involving circles.
| 3. Can angles at the centre of a circle be used to find the circumference or area of the circle? |  |
Ans. Angles at the centre of a circle are not directly used to find the circumference or area of the circle. They are mainly used to find missing angles within the circle and to solve geometry problems involving circles.
| 4. How do angles at the centre of a circle relate to the concept of a semicircle? |  |
Ans. In a semicircle, the angle at the centre is always 90 degrees. This means that the angle at the centre of a semicircle is half of a full circle, which is 180 degrees.
| 5. Are angles at the centre of a circle important in the study of circle theorems? |  |
Ans. Yes, angles at the centre of a circle play a significant role in the study of circle theorems. They are used to prove various theorems and properties of circles in geometry.
Related Searches
















