Gauss Law & Its Applications | Physics Class 12 - NEET PDF Download
Gauss Law states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity.
The electric flux in an area is defined as the electric field multiplied by the area of the surface projected in a plane and perpendicular to the field.
What is Gauss Law?
According to the Gauss law, the total flux linked with a closed surface is 1/ε0 times the charge enclosed by the closed surface.
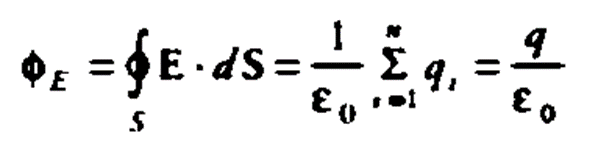
- For example, a point charge q is placed inside a cube of edge ‘a’. Now as per Gauss law, the flux through each face of the cube is q/6ε0.
- The electric field is the basic concept to know about electricity. Generally, the electric field of the surface is calculated by applying Coulomb’s law, but to calculate the electric field distribution in a closed surface, we need to understand the concept of Gauss law.
- It explains the electric charge enclosed in a closed or the electric charge present in the enclosed closed surface.
Gauss Law Formula
As per the Gauss theorem, the total charge enclosed in a closed surface is proportional to the total flux enclosed by the surface. Therefore, if ϕ is total flux and ϵ0 is electric constant, the total electric charge Q enclosed by the surface is;
Q = ϕ ϵ0
The Gauss law formula is expressed by;
ϕ = Q/ϵ0
Where,
Q = total charge within the given surface,
ε0 = the electric constant.
The Gauss Theorem
The net flux through a closed surface is directly proportional to the net charge in the volume enclosed by the closed surface.
Φ = → E.d → A = qnet/ε0
In simple words, the Gauss theorem relates the ‘flow’ of electric field lines (flux) to the charges within the enclosed surface. If there are no charges enclosed by a surface, then the net electric flux remains zero.
This means that the number of electric field lines entering the surface is equal to the field lines leaving the surface.
The Gauss theorem statement also gives an important corollary:
The electric flux from any closed surface is only due to the sources (positive charges) and sinks (negative charges) of electric fields enclosed by the surface. Any charges outside the surface do not contribute to the electric flux. Also, only electric charges can act as sources or sinks of electric fields. Changing magnetic fields, for example, cannot act as sources or sinks of electric fields.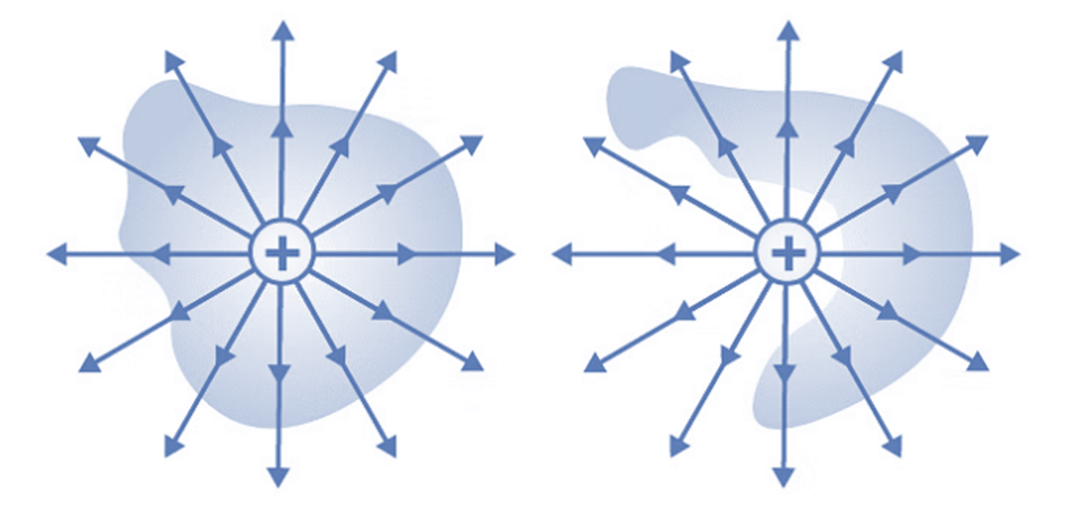 Gauss Law in Magnetism
Gauss Law in Magnetism
The net flux for the surface on the left is non-zero as it encloses a net charge. The net flux for the surface on the right is zero since it does not enclose any charge.
Note: The Gauss law is only a restatement of the Coulombs law. If you apply the Gauss theorem to a point charge enclosed by a sphere, you will get back the Coulomb’s law easily.
Applications of Gauss Law
1. In case of an infinite line of charge, at a distance ‘r’. E = (1/4 × πrε0) (2π/r) = λ/2πrε0. Where λ is the linear charge density.
2. The intensity of the electric field near a plane sheet of charge is E = σ/2ε0K where σ = surface charge density.
3. The intensity of the electric field near a plane charged conductor E = σ/Kε0 in a medium of dielectric constant K. If the dielectric medium is air, then Eair = σ/ε0.
4. The field between two parallel plates of a condenser is E = σ/ε0, where σ is the surface charge density.
Electric Field due to Infinite Wire – Gauss Law Application
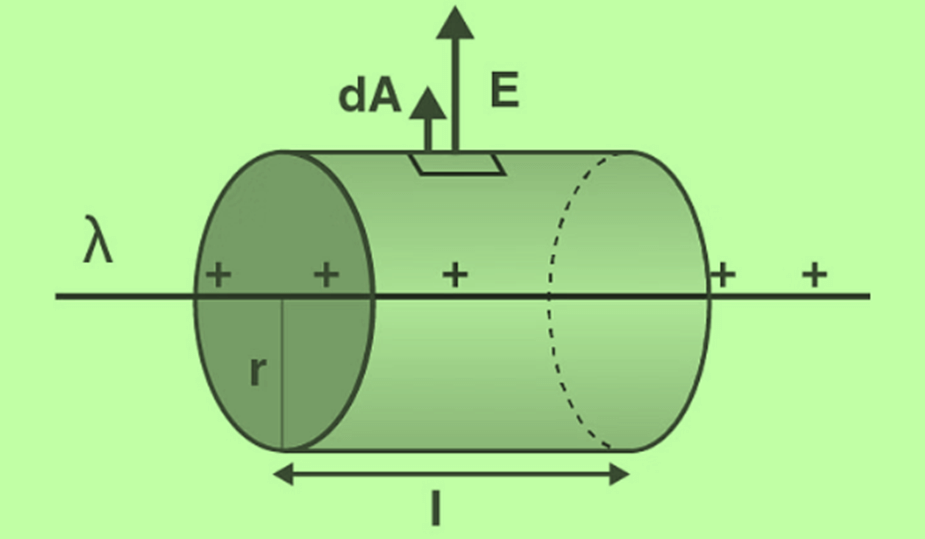
Consider an infinitely long line of charge with the charge per unit length being λ. We can take advantage of the cylindrical symmetry of this situation. By symmetry, The electric fields all point radially away from the line of charge, there is no component parallel to the line of charge.
We can use a cylinder (with an arbitrary radius (r) and length (l)) centred on the line of charge as our Gaussian surface.
 Applications of Gauss Law - Electric Field due to Infinite Wire
Applications of Gauss Law - Electric Field due to Infinite Wire
As you can see in the above diagram, the electric field is perpendicular to the curved surface of the cylinder. Thus, the angle between the electric field and area vector is zero and cos θ = 1
The top and bottom surfaces of the cylinder lie parallel to the electric field. Thus the angle between area vector and the electric field is 90 degrees and cos θ = 0.
Thus, the electric flux is only due to the curved surface
According to Gauss Law,
Φ = → E.d → A
Φ = Φcurved + Φtop + Φbottom
Φ = → E . d → A = ∫E . dA cos 0 + ∫E . dA cos 90° + ∫E . dA cos 90°
Φ = ∫E . dA × 1
Due to radial symmetry, the curved surface is equidistant from the line of charge and the electric field in the surface has a constant magnitude throughout.
Φ = ∫E . dA = E ∫dA = E . 2πrl
The net charge enclosed by the surface is:
qnet = λ.l
Using Gauss theorem,
Φ = E × 2πrl = qnet/ε0 = λl/ε0
E × 2πrl = λl/ε0
E = λ/2πrε0
Problems on Gauss Law
Problem 1: A uniform electric field of magnitude E = 100 N/C exists in the space in X-direction. Using the Gauss theorem calculate the flux of this field through a plane square area of edge 10 cm placed in the Y-Z plane. Take the normal along the positive X-axis to be positive.
Solution: The flux Φ = ∫ E.cosθ ds.
As the normal to the area points along the electric field, θ = 0.
Also, E is uniform so, Φ = E.ΔS = (100 N/C) (0.10m)2 = 1 N-m2.
Problem 2: A large plane charge sheet having surface charge density σ = 2.0 × 10-6 C-m-2 lies in the X-Y plane. Find the flux of the electric field through a circular area of radius 1 cm lying completely in the region where x, y, z are all positive and with its normal making an angle of 600 with the Z-axis.
Solution: The electric field near the plane charge sheet is E = σ/2ε0 in the direction away from the sheet. At the given area, the field is along the Z-axis.
The area = πr2 = 3.14 × 1 cm2 = 3.14 × 10-4 m2.
The angle between the normal to the area and the field is 60o.
Hence, according to Gauss theorem, the flux = E.ΔS cos θ = σ/2ε0 × pr2 cos 60º
= 17.5 N-m2C-1.
Problem 3: The figure shows three concentric thin spherical shells A, B and C of radii a, b, and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.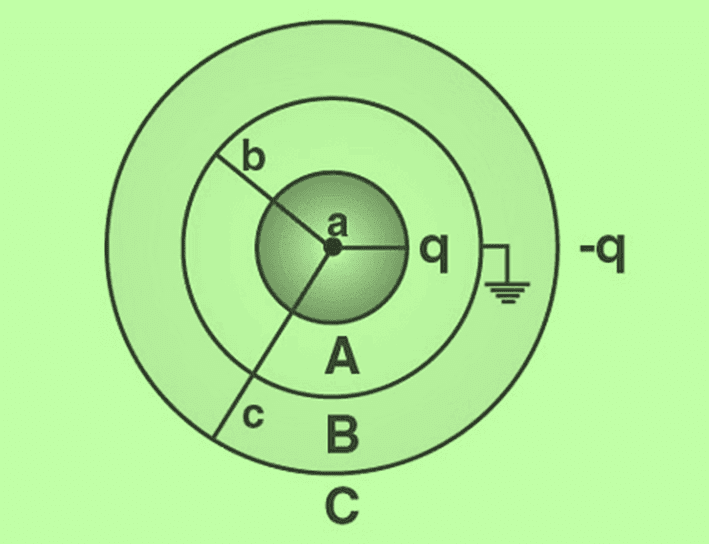 Solution: As shown in the previous worked out example, the inner surface of B must have a charge -q from the Gauss law. Suppose, the outer surface of B has a charge q’.
Solution: As shown in the previous worked out example, the inner surface of B must have a charge -q from the Gauss law. Suppose, the outer surface of B has a charge q’.
The inner surface of C must have a charge -q’ from Gauss law. As the net charge on C must be -q, its outer surface should have a charge q’ – q. The charge distribution is shown in the figure.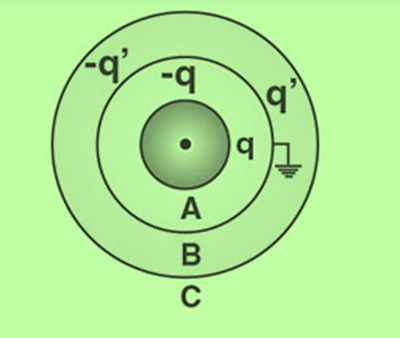
The potential at B,
- Due to the charge q on A = q/4πε0b,
- Due to the charge -q on the inner surface of B = -q/4πε0b,
- Due to the charge q’ on the outer surface of B = q’/4πε0b,
- Due to the charge -q’, on the inner surface of C = -q’/4πε0c,
- Due to the charge q’ – q on the outer surface of C = (q’ – q)/4πε0c.
The net potential is, VB = q’/4πε0b – q/4πε0c
This should be zero as the shell B is earthed. Thus, q’ = q × b/c
The charges on various surfaces are as shown in the figure: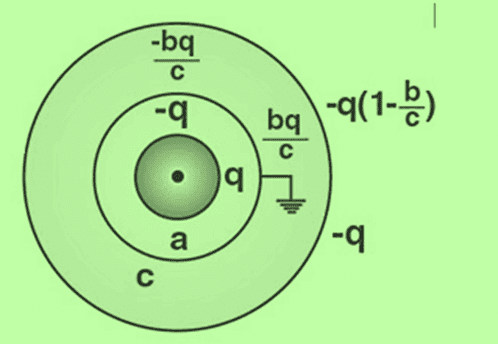
Problem 4: A particle of mass 5 × 10-6g is kept over a large horizontal sheet of charge of density 4.0 × 10-6 C/m2 (figure). What charge should be given to this particle so that if released, it does not fall down? How many electrons are to be removed to give this charge? How much mass is decreased due to the removal of these electrons?
Solution: The electric field in front of the sheet is,
E = σ/2ε0 = (4.0 × 10-6)/(2 × 8.85 × 10-12) = 2.26 × 105 N/C
If a charge q is given to the particle, the electric force qE acts in the upward direction. It will balance the weight of the particle if
q × 2.26 × 105 N/C = 5 × 10-9 kg × 9.8 m/s2
or, q = [4.9 × 10-8]/[2.26 × 105]C = 2.21 × 10-13 C
The charge on one electron is 1.6 × 10-19C. The number of electrons to be removed;
= [2.21 × 10-13]/[1.6 × 10-19] = 1.4 × 106
Mass decreased due to the removal of these electrons = 1.4 × 106 × 9.1 × 10-31 kg = 1.3 × 10-24 kg.
Problem 5: Two conducting plates A and B are placed parallel to each other. A is given a charge Q1 and B a charge Q2. Find the distribution of charges on the four surfaces.
Solution: 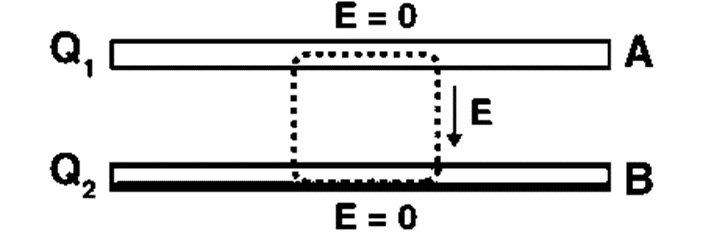
Consider a Gaussian surface as shown in figure (a). Two faces of this closed surface lie completely inside the conductor where the electric field is zero.
The flux through these faces is, therefore, zero. The other parts of the closed surface which are outside the conductor are parallel to the electric field and hence the flux on these parts is also zero.
The total flux of the electric field through the closed surface is, therefore, zero. From Gauss law, the total charge inside the closed surface should be zero. The charge on the inner surface of A should be equal and opposite to that on the inner surface of B.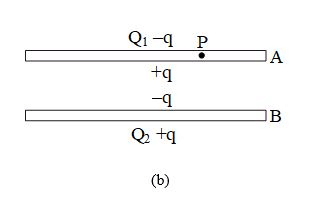
The distribution should be like the one shown in figure (b). To find the value of q, consider the field at a point P inside the plate A. Suppose, the surface area of the plate (one side) is A.
Using the equation E = σ/2ε0, the electric field at P;
- Due to the charge Q1 – q = (Q1 – q)/2Aε0 (downward),
- Due to the charge +q = q/2Aε0 (upward),
- Due to the charge -q = q/2Aε0 (downward),
- Due to the charge Q2 + q = (Q2 + q)/2Aε0 (upward).
The net electric field at P due to all the four charged surfaces is (in the downward direction)
(Q1 – q)/2Aε0 – q/2Aε0 + q/2Aε0 – (Q2 + q)/2Aε0
As the point P is inside the conductor, this field is should be zero.
Hence, Q1 – q – Q2 – q = 0
or q = (Q1 – Q2)/2 . . . . . (i)
Thus, Q1 – q = (Q1 + Q2)/2 . . . . . . (ii)
and Q2 + q = [Q1 + Q]2/2
Using these equations, the distribution shown in the figure (a, b) can be redrawn as in the figure.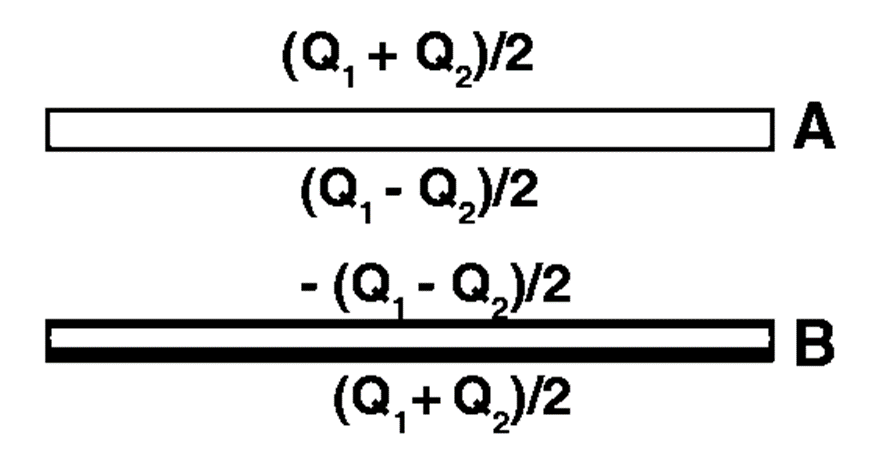
This result is a special case of the following result. When charged conducting plates are placed parallel to each other, the two outermost surfaces get equal charges and the facing surfaces get equal and opposite charges.
Problem 6: A solid conducting sphere having a charge Q is surrounded by an uncharged concentric conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of hollow shell be V. What will be the new potential difference between the same two surfaces if the shell is given a charge -3Q?
Solution: In case of a charged conducting sphere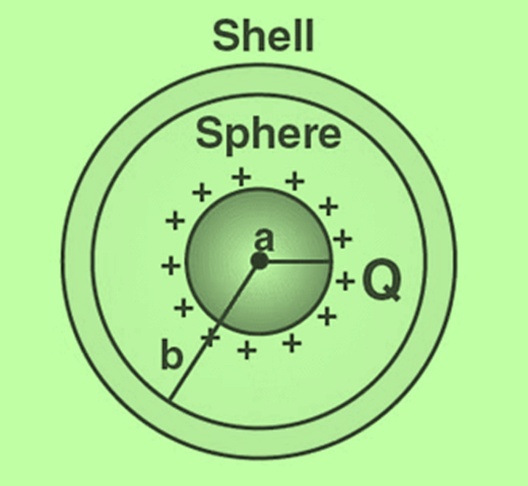
Vin = Vc = Vs = 1/4πε0
and Vout = 1/4πε0
So if a and b are the radii of a sphere and spherical shell respectively, the potential at their surfaces will be;
Vsphere = 1/4πε0 [Q/a] and Vshell = 1/4πε0 [Q/b] and so according to the given problem;
V = V’sphere – V’shell = Q/4πε0 [1/a – 1/b] = V . . . . . . . (1)
Now when the shell is given a charge (-3Q) the potential at its surface and also inside will change by;
V0 = 1/4πε0 [ -3Q/b]
So that now,
V’sphere = 1/4πε0 [Q/a + V0] and V’shell = 1/4πε0 [Q/b + V0]
Hence, V’sphere – V’shell = Q/4πε0 [1/a – 1/b] = V [from Eqn. (1)]
i.e., if any charge is given to external shell the potential difference between sphere and shell will not change.
This is because by the presence of charge on the outer shell, potential everywhere inside and on the surface of the shell will change by the same amount and hence the potential difference between sphere and shell will remain unchanged.
Problem 7: A very small sphere of mass 80 g having a charge q is held at height 9 m vertically above the centre of a fixed non conducting sphere of radius 1 m, carrying an equal charge q. When released it falls until it is repelled just before it comes in contact with the sphere. Calculate the charge q. [g = 9.8 m/s2]
Solution: Keeping in mind that here both electric and gravitational potential energy is changing and for an external point, a charged sphere behaves as the whole of its charge were concentrated at its centre.
Applying the law of conservation of energy between initial and final position, we have
1/4πε0 × (q.q/9) + mg × 9 = 1/4πε0 × (q2/1) + mg × 1
or, q2 = (80 × 10-3 × 9.8)/109 = 28μC.
Frequently Asked Questions on Gauss Law
1. How is Gauss law Related to Coulomb’s law?
One of the fundamental relationships between the two laws is that Gauss law can be used to derive Coulomb’s law and vice versa. We can further say that Coulomb’s law is equivalent to Gauss’s law meaning they are almost the same thing. While this relation is discussed extensively in electrodynamics we will look at a derivation with the help of an example.
Let’s take a point charge q. Now if we apply Coulomb’s law the electric field generated is given by:
E = kq/r2
where k=1 /4πϵ0. If we take the sphere of the radius (r) that is centred on charge q. Now for the surface S of this sphere, we will have: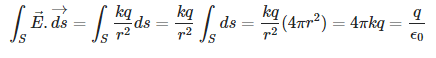
At the end of the equation, we can see that it refers to Gauss law. All in all, we can determine the relation between Gauss law and Coulomb’s law by deducing the spherical symmetry of the electric field and by performing the integration.
2. How do we choose an appropriate Gaussian Surface for different cases?
In order to choose an appropriate Gaussian Surface, we have to take into account the states that the ratio of charge and the dielectric constant is given by a (two-dimensional) surface integral over the electric field symmetry of the charge distribution. There are three different cases that we will need to know.
- Spherical, when the charge distribution is spherically symmetric.
- Cylindrical, when the charge distribution is cylindrically symmetric.
- Pillbox, when the charge distribution has translational symmetry along a plane.
We can choose the size of the surface depending on where we want to calculate the field. Gauss theorem is helpful for finding field when there is a certain symmetry as it tells us how the field is directed.
3. How is electric flux related to Gauss law?
When we talk about the relation between electric flux and Gauss law, the law states that the net electric flux in a closed surface will be zero if the volume that is defined by the surface contains a net charge.
To establish the relation we will first take a look at the Gauss law.
If we take the Gauss’s law it is represented as:
ΦE = Q/εo
Here,
- ΦE = electric flux through a closed surface S enclosing any volume V.
- Q = total charge enclosed within V,
- εo = electric constant.
Meanwhile, the electric flux ΦE can now be defined as a surface integral of the electric field. It is given as:
ΦE = ∫∫ E . dA
Here,
- E = electric field.
- dA = vector representing an infinitesimal element of area of the surface.
Notably, flux is considered as an integral of the electric field. This relation or form of Gauss’s law is known as the integral form.
4. What is the differential form of Gauss theorem?
The differential form of Gauss law relates the electric field to the charge distribution at a particular point in space. To elaborate, as per the law, the divergence of the electric field (E) will be equal to the volume charge density (p) at a particular point. It is represented as:
ΔE = ρ/εo
Here,
εo = permittivity of free space.
5. How to find the electric field using Gauss law?
Normally, the Gauss law is used to determine the electric field of charge distributions with symmetry. There are several steps involved in solving the problem of the electric field with this law. They are as follows:
- First, we have to identify the spatial symmetry of the charge distribution.
- The next step involves choosing a correct Gaussian surface with the same symmetry as the charge distribution. Its consequences should also be identified.
- Evaluate the integral ΦsE over the Gaussian surface and then calculate the flux through the surface.
- Find the amount of charge enclosed by the Gaussian surface.
- Evaluate the electric field of the charge distribution.
However, students have to keep in mind the three types of symmetry in order to determine the electric field. The types of symmetry are:
- Spherical symmetry
- Cylindrical symmetry
- Planar symmetry
|
74 videos|314 docs|88 tests
|
FAQs on Gauss Law & Its Applications - Physics Class 12 - NEET
| 1. What is Gauss Law? |  |
| 2. What are the applications of Gauss Law? |  |
| 3. How is Gauss Law derived? |  |
| 4. Can Gauss Law be applied to magnetic fields? |  |
| 5. What are the limitations of Gauss Law? |  |

















