Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Arcs & Sectors
Arcs & Sectors | Mathematics for GCSE/IGCSE - Class 10 PDF Download
What is an arc?
- An arc is a portion of the circle's circumference.
- Two points on a circle's circumference will form two arcs.
- The smaller arc is called the minor arc, while the larger one is known as the major arc.
Question for Arcs & SectorsTry yourself: What is the definition of an arc?View Solution
What is a sector?
- In technical language, a sector refers to the portion of a circle that is enclosed by two radii and an arc.
- It's simpler to envision a sector as resembling a slice of circular pizza, cake, or pie, with the arc representing the curved edge (similar to the crust).
- When two radii are drawn within a circle, they form two sectors.
- The smaller sector is termed the minor sector, while the larger one is called the major sector.
- If the angle of the slice is represented by θ (the Greek letter "theta"), then the formulas for the sector's area and the arc's length are fractions derived from the circle's area and circumference.
- It's important to note that a complete circle comprises 360°, thus the fraction signifies the angle out of 360°.
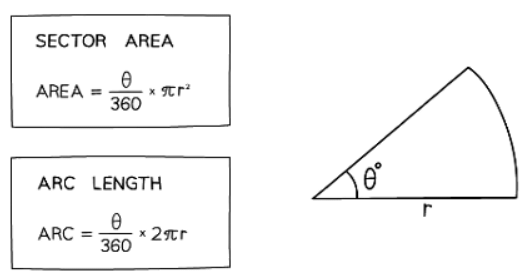
- If memorizing formulas isn't your forte, there's a rationale behind these two.
- It's essential to recall the formulas for circumference and area.
- Subsequently, the process involves determining a fraction of the entire circle – denoted as "θ out of 360."
- Utilizing sector and arc formulas follows a similar logic to any other formulaic approach.
- Jot down what you're aware of and what you aim to ascertain.
- Select the appropriate formula.
- Substitute the known values and solve for the desired outcome.
The document Arcs & Sectors | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
FAQs on Arcs & Sectors - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the formula to find the length of an arc on a circle? |  |
Ans. The formula to find the length of an arc on a circle is given by: Length of arc = 2πr (θ/360), where r is the radius of the circle and θ is the angle in degrees.
| 2. How do you calculate the area of a sector on a circle? |  |
Ans. The formula to calculate the area of a sector on a circle is: Area of sector = 0.5r^2 (θ/360), where r is the radius of the circle and θ is the angle in degrees.
| 3. Can you explain the relationship between circle angle and fraction in terms of arcs and sectors? |  |
Ans. The angle subtended by an arc at the center of a circle is directly proportional to the fraction of the circumference of the circle that the arc represents. This relationship is key in understanding how to calculate arc lengths and sector areas.
| 4. What are some important formulas to remember when dealing with arcs and sectors in circle geometry? |  |
Ans. Some important formulas to remember include: length of arc = 2πr (θ/360), area of sector = 0.5r^2 (θ/360), and the relationship between circle angle and fraction in terms of arcs and sectors.
| 5. How can I test my understanding of arcs and sectors in preparation for my IGCSE Maths exam? |  |
Ans. You can test your understanding by practicing past exam questions that involve calculating arc lengths, sector areas, and applying the formulas related to arcs and sectors in circle geometry. This will help you familiarize yourself with the concepts and improve your problem-solving skills.
Related Searches





















