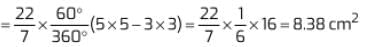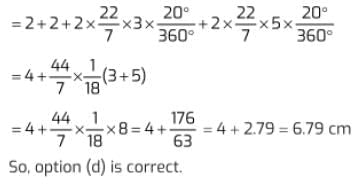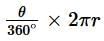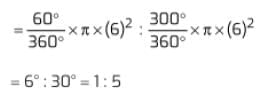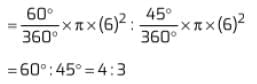Assignment: Areas Related to Circles | Mathematics (Maths) Class 10 PDF Download
Multiple choice Questions
Q1. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. The length of the arc is;
(a) 20 cm
(b) 21 cm
(c) 22 cm
(d) 25 cm
Ans. (c) 22 cm
Length of an arc = (θ/360°) × (2πr)
∴ Length of an arc AB = (60°/360°) × 2 × 22/7 × 21
= (1/6) × 2 × (22/7) × 21
Or Arc AB Length = 22cm
Q2. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. The area of the sector formed by the arc is:
(a) 200 cm2
(b) 220 cm2
(c) 231 cm2
(d) 250 cm2
Ans. (c) 231 cm2
The angle subtended by the arc = 60°
So, area of the sector = (60°/360°) × π r2 cm2
= (441/6) × (22/7) cm2
= 231 cm2
Q3. Area of a sector of angle p (in degrees) of a circle with radius R is
(a) p/180 × 2πR
(b) p/180 × π R2
(c) p/360 × 2πR
(d) p/720 × 2πR2
Ans. (d) p/720 × 2πR2
The area of a sector = (θ/360°) × π r2
Given, θ = p
So, area of sector = p/360 × π R2
Multiplying and dividing by 2 simultaneously,
= [(p/360)/(π R2)]×[2/2]
= (p/720) × 2πR2
Q4. If the area of a circle is 154 cm2, then its perimeter is
(a) 11 cm
(b) 22 cm
(c) 44 cm
(d) 55 cm
Ans. (c) 44 cm
Given,
Area of a circle = 154 cm2
πr2 = 154
(22/7) × r2 = 154
r2 = (154 × 7)/22
r2 = 7 × 7
r = 7 cm
Perimeter of circle = 2πr = 2 × (22/7) × 7 = 44 cm
Q5: If θ is the angle (in degrees) of a sector of a circle of radius r, then the length of arc is
(a) (πr2θ)/360
(b) (πr2θ)/180
(c) (2πrθ)/360
(d) (2πrθ)/180
Ans. (a) (2πrθ)/360
If θ is the angle (in degrees) of a sector of a circle of radius r, then the area of the sector is (2πrθ)/360.
Case-Based Questions
Case Study 1:
Sara hold a Japanese folding fan in her hand as shown in the figure. It is shaped like a sector of a circle and made of a thin material such as paper or feather. The inner and outer radii are 3 cm and 5 cm respectively. The fan has three colours, i.e., red, blue and green.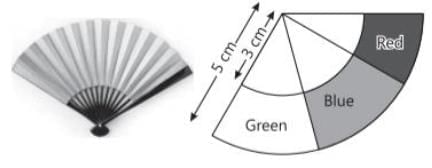
Based on the above information, solve the following questions:
Q1. If the region containing blue colour makes an angle of 80° at the centre, the area of the region having blue colour is:
(a) 9.17 cm²
(a) 0.1 cm²
(a) 11.17 cm²
(a) 13.17 cm²
Ans. (c)
Area of the region containing blue colour
So, option (c) is correct.
Q2. If the region containing green colour makes an angle of 60° at the centre, the area of the region having green colour is:
(a) 6.2 cm²
(b) 8.38 cm²
(c) 9.9 cm²
(d) 11.12 cm²
Ans. (b)
Area of the region containing green colour
So, option (b) is correct.
Q3. If the region containing red colour makes an angle of 20° at the centre, the perimeter of the region containing red colour is:
(a) 2.9 cm
(a) 4.2 cm
(a) 5.4 cm
(a) 6.79 cm
Ans. (d)
Perimeter of the region containing red colour (5-3)+(5-3)+ length of arc of sector having radius 3 cm + length of arc of sector having radius 5 cm
Q4. The region given in the figure represents:
(a) Minor sector
(b) major sector
(c) Minor segment
(d) Major segment
Ans. (a)
Angle of given sector =80° + 60° + 20° = 160° Thus, the given region represents minor sector of a circle.
So, option (a) is correct.
Case Study 2:
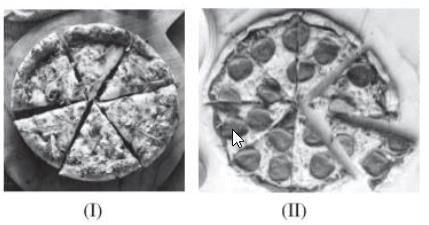
We all love to eat pizzas, especially kids and a variety of pizzas are available in India which have been modified according to Indian taste and menu. From the Greeks to the Egyptians, from the Persians to the Indians, there have been incarnations of pizza served throughout history, Flatbreads, naan and plakountos are all early preparations that could be considered cousins to the modern pizza, but there isn't a consensus as to which is first and whether these could even be considered precursors to pizza at all. Consider two pizzas, both of equal diameter, namely, 12 inches. The first pizza marked (I) has been cut into six equal slices, whereas the second pizza, marked (II) has been cut into eight equal slices.
Based on the above information, solve the following questions:
Q1. The area of one slice in pizza, marked (I) is:
(a) 6π sq. inches
(b) 8π sq. inches
(c) 10π sq. inches
(d) None of these
Ans. (a)
Area of sector of a circle = (θ/360°) × πr²
where, θ is the angle subtended by the sector at the centre. The radius of pizza (r) is 6 inches and as the pizza has been cut into six equal slices, the angle (θ) subtended at the centre is equal = 360°/6, i.e., to 60°.
∴ Required area = 60°/360° × π × 6² = 6π sq. inches.
So, option (a) is correct.
Q2. The perimeter of the pizza slice shown in (1) is:
(a) (π + 12) inch
(b) (π + 10) inch
(c) (2π + 10) inch
(d) (2π + 12) inch
Ans. (d)
Perimeter of a sector = l + 2r, where l is the length of the arc given by
here, θ = 60º and r = 6 inch
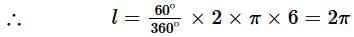
and
2r = 2 x 6 = 12
∴ Perimeter of pizza = (2π + 12) inch
So, option (d) is correct.
Q3. The ratio of area of slice to the area of remaining pizza in (1) is:
(a) 5:1
(b) 1:5
(c) 2:5
(d) 5:3
Ans. (b)
The angle subtended by a slice of pizza (1) at the centre is 60°. Therefore, angle subtended by the remaining pizza at the centre is 300°.
∴ Ratio of areas of minor sector and major sector
So, option (b) is correct
Q4. The ratio of areas of each slice of pizza (I) and (II) is:
(a) 3:4
(b) 5:3
(c) 4:3
(d) 2:5
Ans. (c)
The angle subtended by a slice in pizza (I) is 60°,
and the angle subtended by a slice in pizza (II) is 45°
i.e 360º/8Therefore, ratio of area of slice in the two cases
So. option (c) is correct.
Q5. The relation between area of a sector (A), length of the arc (l), angle (θ) subtended by the arc at the centre and radius of circle is:
(a) (1/2)lr
(b) lr
(c) (1/3)lr
(d) (1/2)r²
Ans. (a)
The area of sector is given by 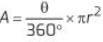
and
length of the arc is given by 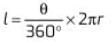
Multiplying and dividing A by 2. we get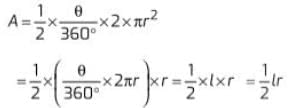
So. option (a) is correct.
|
127 videos|584 docs|79 tests
|
FAQs on Assignment: Areas Related to Circles - Mathematics (Maths) Class 10
| 1. What is the formula for calculating the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. What is the relationship between the radius, diameter, and area of a circle? |  |
| 4. How do you calculate the length of an arc in a circle? |  |
| 5. What are the different parts of a circle, and what are their definitions? |  |