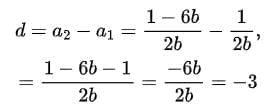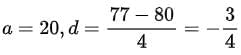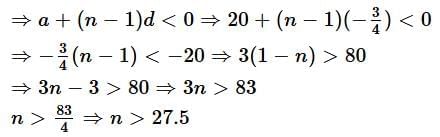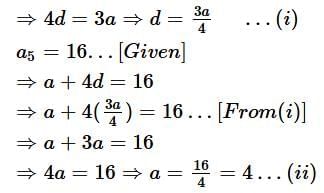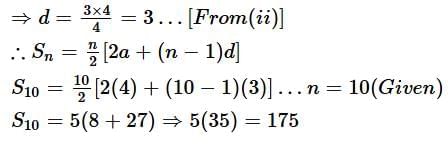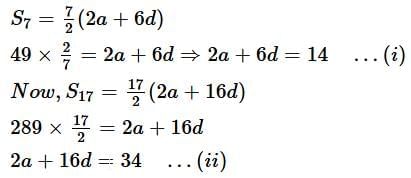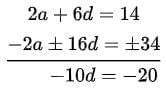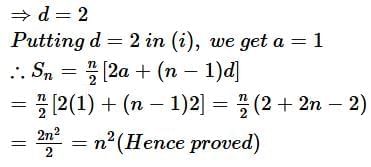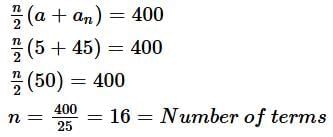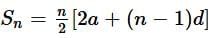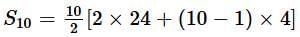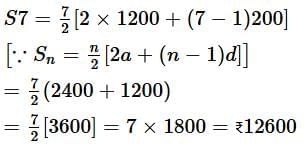Assignment: Arithmetic Progressions | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Multiple Choice Questions |

|
| Short Answer Questions |

|
| Long Answer Questions |

|
| Case-Based Questions |

|
Multiple Choice Questions
Q1. In an Arithmetic Progression, if a = 28, d = -4, n = 7, then an is:
(a) 4
(b) 5
(c) 3
(d) 7
Ans. (a) 4
For an AP,
an = a+(n-1)d
= 28+(7-1)(-4)
= 28+6(-4)
= 28-24
an=4
Q2. If a = 10 and d = 10, then first four terms will be:
(a) 10, 30, 50, 60
(b) 10, 20, 30, 40
(c) 10, 15, 20, 25
(d) 10, 18, 20, 30
Ans. (b) 10, 20, 30, 40
a = 10, d = 10
a1 = a = 10
a2 = a1+d = 10+10 = 20
a3 = a2+d = 20+10 = 30
a4 = a3+d = 30+10 = 40
Q3. The first term and common difference for the A.P. 3, 1, -1, -3 is:
(a) 1 and 3
(b) -1 and 3
(c) 3 and -2
(d) 2 and 3
Ans. (c) 3 and -2
First term, a = 3
Common difference, d = Second term – First term
⇒ 1 – 3 = -2
⇒ d = -2
Q4. The 21st term of AP whose first two terms are -3 and 4 is:
(a) 17
(b) 137
(c) 143
(d) -143
Ans. (b) 137
First term = -3 and second term = 4
a = -3
d = 4 - a = 4 - ( - 3) = 7
a21 = a + (21-1)d
= -3 + (20)7
= -3 + 140
= 137
Q5. The missing terms in AP: __, 13, __, 3 are:
(a) 11 and 9
(b) 17 and 9
(c) 18 and 8
(d) 18 and 9
Ans. (c)
a2 = 13 and
a4 = 3
The nth term of an AP;
an = a + (n−1) d
a2 = a + (2-1)d
13 = a + d ………………. (i)
a4 = a + (4-1)d
3 = a + 3d ………….. (ii)
Subtracting equation (i) from (ii), we get,
– 10 = 2d
d = – 5
Now put value of d in equation 1
13 = a + (-5)
a = 18 (first term)
a3 = 18 + (3-1)(-5)
= 18 + 2(-5) = 18 - 10 = 8 (third term).
Short Answer Questions
Q1. Find the 9th term from the end (towards the first term) of the A.P. 5,9,13, …, 185.
Here, First term, a = 5
Common difference, d = 9 – 5 = 4
Last term, 1 = 185
nth term from the end = l – (n – 1)d
9th term from the end = 185 – (9 – 1)4
= 185 – 8 × 4 = 185 – 32 = 153
Q2. Find the common difference of the A.P 
The common difference,
Q3. Which term of the progression 4, 9, 14, 19, … is 109?
Here, d = 9 - 4 = 14 - 9 = 19 – 14 = 5
∴ Difference between consecutive terms is constant.
Hence it is an A.P.
Given: First term, a = 4, d = 5, an = 109 (Let)
∴ an = a + (n – 1) d … [General term of A.P.
∴ 109 = 4 + (n – 1) 5
⇒ 109 – 4 = (n – 1) 5
Q4. Which term of the progression 20, 192, 183, 17 ..... is the first negative term?
Given: A.P.:
Here
For first negative term, an < 0
∴ Its negative term is 28th term.
Q5. Find the sum of all three digit natural numbers, which are multiples of 11.
To find: 110 + 121 + 132 + … + 990
Here a = 110, d = 121- 110 = 11, an = 990
∴ a + (n – 1)d = 990
110 + (n – 1).11 = 990
(n – 1). 11 = 990 – 110 = 880
(n – 1) = 880 = 80
n = 80 + 1 = 81
As Sₙ = (n/2)(a₁ + aₙ)
∴ S₈₁ = (81/2)(110 + 990)
= (81/2)(1100)
= 81 × 550
= 44,550
Long Answer Questions
Q1. The 13th term of an AP is four times its 3rd term. If its 5th term is 16, then find the sum of its first ten terms.
a13 = 4a3 [Given]
⇒ a + 12d = 4(a + 2d) ..... [an = a + (n - 1)d]
⇒ a + 12d - 4a - 8d = 0
putting a = 4 in (i), we get a = 3
Q2. If the sum of first 7 terms of an A.P is 49 and that of its first 17 terms is 289, find the sum of first n terms of the A.P. (2016D)
Let 1st term = a, Common difference = d
Given: S7 = 49, S17 = 289
As we know, Sn = n/2 [2a + (n - 1)d]
Solving (i) and (ii), we get
Q3. The first term of an A.P. is 5, the last term is 45 and the sum of all its terms is 400. Find the number of terms and the common difference of the A.P.
First term, a = 5, Last term, an = 45
Let the number of terms = n
Sn = 400
Now, an = 45
a + (n - 1)d = an
5 + (16 - 1)d = 45
15d = 45 - 5
∴ d = 40/15 = 8/3
Case-Based Questions
While playing a treasure hunt game, some clues (numbers) are hidden in various spots collectively forms an AP. If the number on the nth spot is 20 + 4n, then answer the following questions to help the player in spotting the clues. 
Based on the given information, solve the following questions:
Q1. Which number is on the first spot?
(a) 20
(b) 24
(c) 16
(d) 28
Ans. (b)
Given, number on nth spot = 20 + 4n
i.e.. an=20 + 4n
.. Number on first spot, a1 = 20 + 4 (1)
= 20 + 4 = 24
So, option (b) is correct.
Q2. The common difference of the given AP, is:
(a) 20
(b) 4
(c) 16
(d) 24
Ans. (b)
The common difference (d) = an-an-1
⇒ d = 20 + 4n - {20+ (n-1)} [an = 20 + 4n]
= 20 + 4n - 20 - 4n + 4 = 4
So, option (b) is correct.
Q3. Which number is on the (n-2)th spot?
(a) 16 + 4n
(b) 24 + 4n
(c) 12 + 4n
(d) 28 + 4n
Ans. (c)
The number on (n-2)th spot,
an-2 = 20 + 4(n - 2) (: an= 20 + 4n]
= 20 + 4n - 8
= 12 + 4n
So, option (c) is correct.
Q4. What is the sum of all the numbers on the first 10 spots?
(a) 410
(b) 420
(c) 480
(d) 430
Ans. (b)
The sum of first n term of an AP
:- The sum of all the numbers on the first 10 spots,= 5 (48 + 36)
= 5 x 84 = 420
So, option (b) is correct.
Q5. Which spot is numbered as 116?
(a) 5th
(b) 8th
(c) 9th
(d) 24th
Ans. (d)
Let nth spot is numbered as 116.
an = 116 ⇒ 20 + 4n = 116
4n = 96 ⇒ n = 24.
:- 24th spot is numbered as 116.
So, option (d) is correct.
Your younger sister wants to buy an electric car and plans to take loan from a bank for her electric car. She repays her total loan of 321600 by paying every month starting with the first instalment of Rs 2000 and it increases the instalment by Rs 200 every month. 
Based on the above information, solve the following questions:
Q1. Find the list of the instalment formed by the given statement.
(a) 2000, 1800, 1600....
(b) 2000, 2200, 2400....
(c) 2200, 2400, 2600....
(d) 2300, 2600, 2900,...
Ans. (b)
It can be observed that these instalments are in AP having first term (instalment) as 2000 and common difference (increase instalment) as ₹200.
Here, a = 2000 and d = 200
Therefore list of an AP is a, a + d, a + 2d, ...
i.e., 2000, 2000+ 200, 2000 + 2 x 200, ...
i.e., 2000, 2200, 2400,...
So, option (b) is correct.
Q2. The amount paid by her in 25th instalment is:
(a) 6800
(b) 3500
(c) 4800
(d) 6600
Ans. (a)
It can be observed that these instalments are in an AP having first term (instalment) as Rs. 2000 and common difference (increase instalment) as Rs. 200.
Here, a = 2000 and d = 200
.. The amount paid by her in 25th instalment is
T25 = a + (25 - 1)d
=2000 + 24 x 200
= 2000 + 4800 * 6800
So, option (a) is correct.
Q3. Find the difference of the amount in 4th and 6th instalment paid by the younger sister.
(a) Rs 200
(b) Rs 400
(c) Rs 600
(d) Rs 800
Ans.(b)
Let a and d be the first term and common difference of an AP.
Then, a4=a + (4 - 1)d [:- a,= a + (n - 1)d)
= a+3d
Similarly, a = a + 5d.
.. Required difference = a6 - a4
=(a + 5d) - (a + 3d) = 2d
=2 × 200 = 400
So, option (b) is correct.
Q4. In how many instalments does she clear her total bank loan?
(a) 1582
(b) 1580
(c) 1599
(d) 1600
Ans. (c)
Let in n instalments, she clear her loan.
Given,
Tn = 321600
Tn = a + (n - 1)d
321600 = 2000 + (n - 1)200
⇒ 321600 - 2000 = (n - 1)200
⇒ 319600 = (n - 1)200
⇒ 319600/200 = n - 1
⇒ 1598 = n - 1
⇒ n = 1599 So, in 1599 instalments, she clear her bank loan.
So, option (c) is correct.
Q5. Find the sum of the first seven instalments.
(a) Rs 14,000
(b) Rs 13,600
(c) Rs 10,400
(d) Rs 12,600
Ans.(d)
Here, a = 1200, d = 200
.. The sum of first seven instalments is
|
127 videos|685 docs|84 tests
|
FAQs on Assignment: Arithmetic Progressions - Mathematics (Maths) Class 10
| 1. What is an arithmetic progression (AP) and how is it defined mathematically? |  |
| 2. How can we find the sum of the first n terms of an arithmetic progression? |  |
| 3. Can you provide an example of an arithmetic progression and calculate its sum? |  |
| 4. What are some real-world applications of arithmetic progressions? |  |
| 5. How do you identify whether a given sequence is an arithmetic progression? |  |