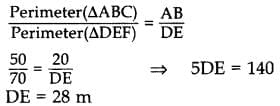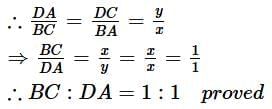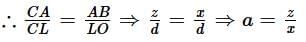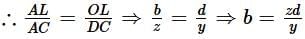Assignment: Triangles | Mathematics (Maths) Class 10 PDF Download
Q1. If ABC and DEF are two triangles and AB/DE = BC/FD, then the two triangles are similar if
(a) ∠A = ∠F
(b) ∠B = ∠D
(c) ∠A = ∠D
(d) ∠B = ∠E
Ans. (b) ∠B =∠D
If ABC and DEF are two triangles and AB/DE=BC/FD, then the two triangles are similar if ∠B =∠D.
Q2. Sides of two similar triangles are in the ratio 4: 9. Areas of these triangles are in the ratio
(a) 2: 3
(b) 4: 9
(c) 81: 16
(d) 16: 81
Ans. (d) 16: 81
Let ABC and DEF are two similar triangles, such that,
ΔABC ~ ΔDEF
And AB/DE = AC/DF = BC/EF = 4/9
As the ratio of the areas of these triangles will be equal to the square of the ratio of the corresponding sides,
∴ Area(ΔABC)/Area(ΔDEF) = AB2/DE2
∴ Area(ΔABC)/Area(ΔDEF) = (4/9)2 = 16/81 = 16: 81
Q3. Which of the following are not similar figures?
(a) Circles
(b) Squares
(c) Equilateral triangles
(d) Isosceles triangles
Ans. (d) Isosceles triangles
All circles, squares, and equilateral triangles are similar figures.
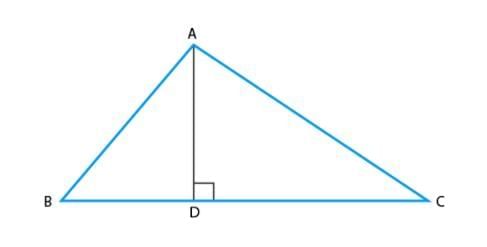
Q4. In triangle ABC, ∠BAC = 90° and AD ⊥ BC. Then
(a) BD . CD = BC2
(b) AB . AC = BC2
(c) BD . CD = AD2
(d) AB . AC = AD2
Ans. (c) BD . CD = AD2
In ΔADB and ΔADC,
∠D = ∠D = 90°
∠DBA = ∠DAC
By AAA similarity criterion,
ΔADB ~ ΔADC
BD/AD = AD/CD
BD.CD = AD2
Q5. If in two triangles ABC and PQR, AB/QR = BC/PR = CA/PQ, then
(a) ΔPQR ~ ΔCAB
(b) ΔPQR ~ ΔABC
(c) ΔCBA ~ ΔPQR
(d) ΔBCA ~ ΔPQR
Ans. (a) ΔPQR ~ ΔCAB
Given that, in triangles ABC and PQR, AB/QR = BC/PR = CA/PQ
If sides of one triangle are proportional to the side of the other triangle, and their corresponding angles are also equal, then both the triangles are similar by SSS similarity. Therefore, ΔPQR ~ ΔCAB
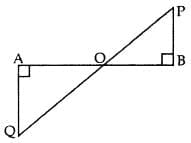
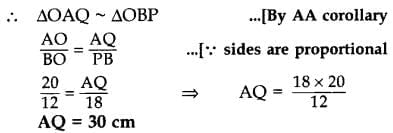
Q6. In the given figure, QA ⊥ AB and PB ⊥ AB. If AO = 20 cm, BO = 12 cm, PB = 18 cm, find AQ
In ∆OAQ and ∆OBP,
∠OAQ = ∠OBP … [Each 90°
∠AOQ = ∠BOP … [vertically opposite angles
Q7. In the given figure, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm.
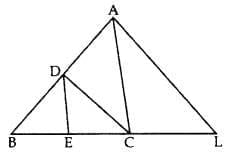
In ∆ABL, CD || LA
Q8. If the perimeters of two similar triangles ABC and DEF are 50 cm and 70 cm respectively and one side of ∆ABC = 20 cm, then find the corresponding side of ∆DEF. (2014)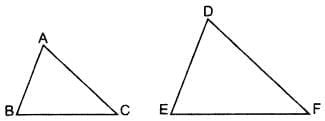
Given. ∆ABC ~ ∆DEF,
Perimeter(∆ABC) = 50 cm
Perimeter(∆DEF) = 70 cm
One side of ∆ABC = 20 cm
To Find. Corresponding side of ∆DEF (i.e.,) DE. ∆ABC ~ ∆DEF …[Given∴ The corresponding side of ADEF = 28 cm
Q9. State whether the given pairs of triangles are similar or not. In case of similarity mention the criterion. 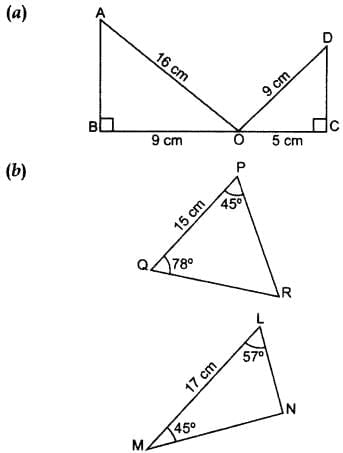
(b) In ∆PQR, ∠P + ∠Q + ∠ZR = 180° …[Angle-Sum Property of a ∆]
45° + 78° + ∠R = 180°
∠R = 180° – 45° – 78° = 57°
In ∆LMN, ∠L + ∠M + ∠N = 180° …[Angle-Sum Property of a ∆]
57° + 45° + ∠N = 180°
∠N = 180° – 57 – 45° = 78°
∠P = ∠M … (each = 45°
∠Q = ∠N … (each = 78°
∠R = ∠L …(each = 57°
∴ ∆PQR – ∆MNL … [By AAA similarity theorem]
Q10. In the given figure, ∆ABC is right-angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE. 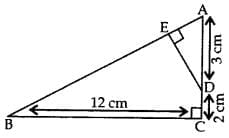
Given: ∆ABC is rt. ∠ed at C and DE ⊥ AB.
AD = 3 cm, DC = 2 cm, BC = 12 cm
To prove:
(i) ∆ABC ~ ∆ADE; (ii) AE = ? and DE = ?
Proof. (i) In ∆ABC and ∆ADE,
∠ACB = ∠AED … [Each 90°]
∠BAC = ∠DAE …(Common)
∴ ∆ABC ~ ∆ADE …[AA Similarity Criterion]
Case Based Questions
Anika is studying in class X. She observe two poles DC and BA. The heights of these poles are x m and y m respectively as shown in figure: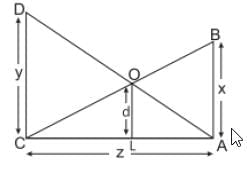 These poles are z m apart and O is the point of intersection of the lines joining the top of each pole to the foot of opposite pole and the distance between point O and L is d. Few questions came to his mind while observing the poles.
These poles are z m apart and O is the point of intersection of the lines joining the top of each pole to the foot of opposite pole and the distance between point O and L is d. Few questions came to his mind while observing the poles.
Based on the above information, solve the following questions:
Q1. Which similarity criteria is applicable in ∆ACAB and CLO?
In ∆CAB and ∆CLO, we have
CAB = <CLO 90°
<C = <C (common)
.. By AA similarity criterion,
∆CAB ~ ∆CLO
Q2. If x=y, prove that BC: DA = 1 : 1.
In ∆DCA and ABAC,
DC = BA [:: x = y (Given)]
<DCA = <BAC [Each 90°)
CA = AC [Common]
By SAS similarity criterian,
∆DCA - ∆BAC
Q3. If CL = a, then find a in terms of x, y and d.
ΔCAB - ΔCLO
ORIn Δ ALO and Δ ACD,
We have
∠ALO = ∠ACD = 90º
∠A = ∠A (common)
∴ By AA similarity criterion,
Δ ALO ∼ Δ ACD
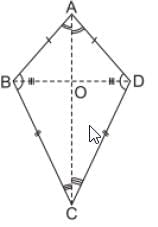
Before Basant Panchami, Samarth is trying to make kites at home. So, he take a rectangular sheet and fold it horizontally, then vertically and fold it transversally. After cutting transversally, he gets a kite shaped figure as shown below: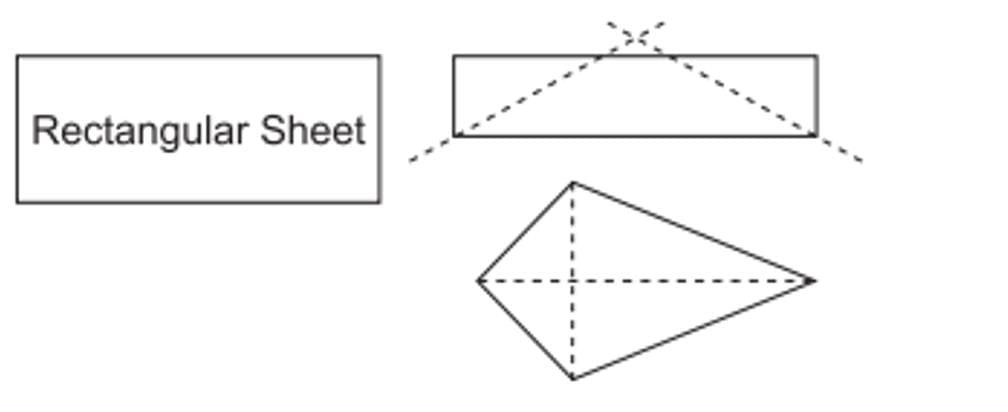 Based on the above information, solve the following questions:
Based on the above information, solve the following questions:
Q1. What is the angle between diagonals of a rectangle?
Diagonals of a rectangle can bisect each other at any angle.
Q2. Prove that two triangles divided by a diagonal in rectangle are similar as well as congruent.
In ∆ABC and ∆CDA AB = CD
<B = <D
BC= DA
∆ABC = ∆CDA
(By SAS) When two triangles are congruent, then they are similar also.
Q3. Prove that the longest diagonal of a kite bisect a pair of opposite angle.
In ΔAOB and ΔAOD,
OA = OA (common)BO = DO (diagonal AC bisect the other diagonal BD)
∴ ΔAOB ∼ ΔAOD (by SSS similarity)
⇒ ∠AOB = ∠DAO ...(1)
In ΔBOC and ΔDOC,
BC = DC
OC = OC (common)
BO = DO
[Diagonal AC bisect the other diagonal BD]
∴ ΔBOC ∼ ΔDOC (by SSS similarity)
⇒ ∠BCO = ∠ DCO ...(2)From (1) and (2), it is clear that, the longest diagonal of a kite bisect a pair of opposite angle.
OR
In Δ ABC and Δ ADC
AB = AD
BC = DC
AC = AC (common)
Δ ABC ∼ Δ ADC (by SSS criterion)
In ΔABC and ΔADC,AB = AD
∠ABC = ∠ADC
BC = DC
∴ ΔABC ~ ΔADC (by SAS criterion)
In ΔABC and ΔADC,
∠B = ∠D
∠BAC = ∠DAC
(∵ ∠BAO = ∠BAC, ∠DAO = ∠DAC, proved above)
∠BAC = ∠DAC(∵ ∠BCO = ∠BCA, ∠DCO = ∠DCA, proved above)
∴ ΔABC ~ ΔADC (by AAA similarity)
Required similarity criterions are SSS, SAS and AAA.
|
127 videos|584 docs|79 tests
|
FAQs on Assignment: Triangles - Mathematics (Maths) Class 10
| 1. What are the different types of triangles based on their sides and angles? |  |
| 2. How do you calculate the area of a triangle? |  |
| 3. What is the Pythagorean theorem and how does it apply to right-angled triangles? |  |
| 4. What are the properties of angles in a triangle? |  |
| 5. How can you determine if three lengths can form a triangle? |  |