Energies of Orbitals & Filling of Orbitals | Chemistry Class 11 - NEET PDF Download
| Table of contents |

|
| The Energy Levels of Electrons in Atoms |

|
| Multielectron Atoms: |

|
| Aufbau Principle |

|
| Pauli Exclusion Principle |

|
| Hund's Rule of Maximum Multiplicity |

|
The Energy Levels of Electrons in Atoms
We can understand the energy levels of electrons in atoms by studying tow different cases of Hydrogen atom and multi-electron atoms.
Hydrogen Atom:
In a hydrogen atom, the energy of an electron is determined solely by the principal quantum number (n). The orbitals with the same principal quantum number have the same energy and are referred to as degenerate. The order of increasing energy is:
- 1s<2s = 2p<3s = 3p = 3d<4s = 4p = 4d = 4f<
Although the shapes of orbitals may vary, electrons in orbitals with the same energy are considered degenerate. The 1s orbital in a hydrogen atom is the ground state, representing the most stable condition. Electrons in 2s, 2p, or higher orbitals are in an excited state, indicating higher energy levels.
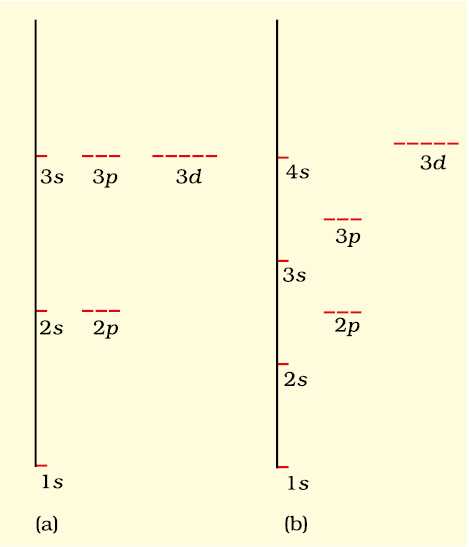 Energy level diagrams for (a) hydrogen atom and (b) multi-electronic atoms
Energy level diagrams for (a) hydrogen atom and (b) multi-electronic atoms
Multielectron Atoms:
- In multi-electron atoms, the energy of an electron depends not only on its principal quantum number (shell) but also on its azimuthal quantum number (subshell). Subshells (s, p, d, f, etc.) with the same principal quantum number have different energies due to mutual repulsion among electrons.
- The shielding effect by inner-shell electrons introduces the concept of effective nuclear charge (Zeff). Despite shielding, the attractive force experienced by outer-shell electrons increases with the nuclear charge. The only electrical interaction present in a hydrogen atom is the attraction between the negatively charged electron and the positively charged nucleus.
- In multi-electron atoms, besides the presence of attraction between the electron and nucleus, there are repulsion terms between every electron and other electrons present in the atom. Thus, the stability of an electron in a multi-electron atom is because total attractive interactions are more than the repulsive interactions. In general, the repulsive interaction of the electrons in the outer shell with the electrons in the inner shell is more important.
- On the other hand, the attractive interactions of an electron increase with the increase of positive charge (Ze) on the nucleus. Due to the presence of electrons in the inner shells, the electron in the outer shell will not experience the full positive charge of the nucleus (Ze). The effect will be lowered due to the partial screening of positive charge on the nucleus by the inner-shell electrons. This is known as the shielding of the outer shell electrons from the nucleus by the inner shell electrons, and the net positive charge experienced by the outer electrons is known as an effective nuclear charge (Zeff ).
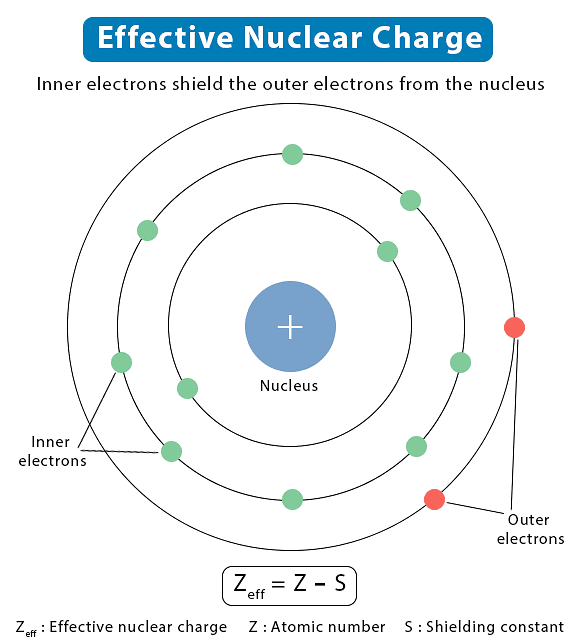 Effective Nuclear Charge
Effective Nuclear Charge
- Despite the shielding of the outer electrons from the nucleus by the inner shell electrons, the attractive force experienced by the outer shell electrons increases with the increase of nuclear charge. In other words, the energy of interaction between the nucleus and electron (orbital energy) decreases (more negative) with the increase of atomic number (Z).
- Both the attractive and repulsive interactions depend upon the shell and shape of the orbital in which the electron is present. For example, electrons present in a spherical-shaped s orbital shield the outer electrons from the nucleus more effectively than electrons present in a p orbital. Similarly, electrons present in p orbitals shield the outer electrons from the nucleus more than electrons present in d orbitals, even though all these orbitals are present in the same shell.
- Further within a shell, due to the spherical shape of s orbital, the s orbital electron spends more time close to the nucleus in comparison to a p orbital electron, which spends more time in the vicinity of the nucleus in comparison to a d orbital electron. In other words, for a given shell (principal quantum number), the effective nuclear charge (Zeff) experienced by the electron decreases with the increase of azimuthal quantum number (l), that is, the s orbital electron will be more tightly bound to the nucleus than the p orbital electron, which in turn will be better tightly bound than the d orbital electron.
- The energy of electrons in an s orbital will be lower (more negative) than that of a p orbital electron, which will have less energy than that of a d orbital electron, and so on. Since the extent of shielding from the nucleus is different for electrons in different orbitals, it leads to the splitting of energy levels within the same shell (or same principal quantum number).
- The energy of an electron in an orbital, as mentioned earlier, depends upon the values of n and l. Mathematically, the dependence of energies of the orbitals on n and l is quite complicated, but one simple rule is that the lower the value of (n + l) for an orbital, the lower is its energy. If two orbitals have the same value of (n + l), the orbital with a lower value of n will have the lower energy.
- It may be noted that different subshells of a particular shell have different energies in the case of multi-electron atoms. However, in a hydrogen atom, these have the same energy. Lastly, it may be mentioned here that energies of the orbitals in the same subshell decrease with an increase in the atomic number. For example, E2s (H) > E2s (Li) > E2s (Na) > E2s (K).
 Arrangement of Orbitals with (n+l) Rule
Arrangement of Orbitals with (n+l) Rule
When electrons are added to the orbitals of different atoms, they follow the aufbau principle. This principle relies on Pauli's exclusion principle, Hund's rule of maximum multiplicity, and the energy levels of the orbitals to determine the arrangement of electrons.
Aufbau Principle
The German word 'aufbau' translates to 'building up.' In the context of orbitals, the term refers to the process of adding electrons to fill up the orbitals.
The Aufbau Rule states that "The electrons are added progressively to various orbitals in the order of increasing energy, starting with the orbital of lowest energy".
The energy of Orbitals:
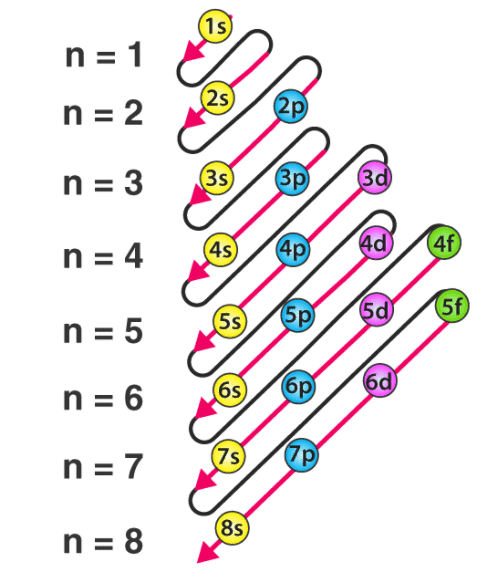 Aufbau Principle
Aufbau Principle
(i) Hydrogen atom: In case of hydrogen atom, energy of orbital is mainly determined by principle quantum number.
For H atom
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p
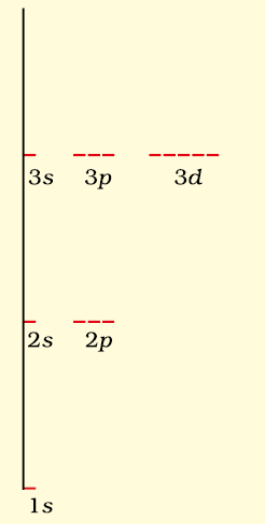 Energy Levels of H-atom
Energy Levels of H-atom
(ii) Multi-electronic atoms: In case of multi-electronic atoms, energy of orbitals depends upon both n and l and hence energy of orbitals is compared on the basis of (n + l) rules generally.
⇒ n + l rule:
(iii) As the value (n + l) increases the total energy of orbitals also increases.
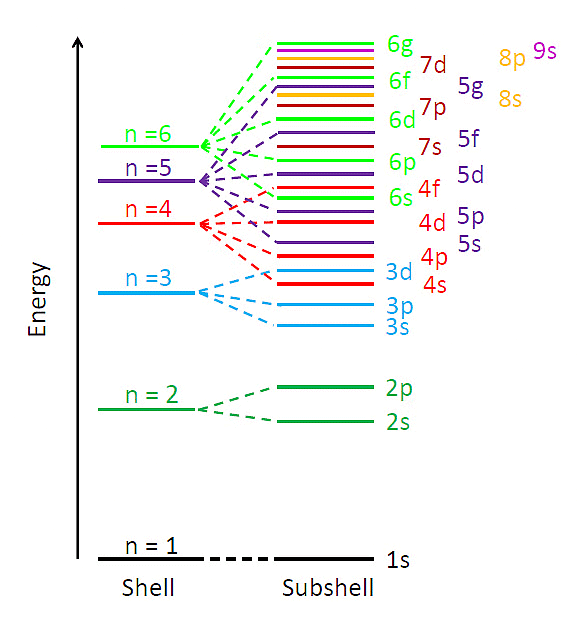 Energy Levels of Multi-Electron Atoms
Energy Levels of Multi-Electron Atoms
(iv) If value of (n + l) is same or different orbital then the orbital with lower value of n, have lower energy.

1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s
Pauli Exclusion Principle
- The principle states that no two electrons in an atom can have same set of all 4 quantum no.
- Therefore spin quantum No. have only two values therefore it can also be commented that orbital can have maximum two electrons with opposite spin.
Hund's Rule of Maximum Multiplicity
While filing the orbitals of same energy (i.e. orbitals of same subshell) pairing of electron start only when each orbital have got 1 electron that too with same spin or parallel spin.
Multiplicity is expressed as 2|s| + 1 where s represent total spin.

 2|s| + 1 = 2
2|s| + 1 = 2

 , 2|s| + 1 = 2
, 2|s| + 1 = 2

 , 2
, 2 + 1 = 4 (It has maximum multiplicity)
+ 1 = 4 (It has maximum multiplicity)
|
127 videos|244 docs|87 tests
|
FAQs on Energies of Orbitals & Filling of Orbitals - Chemistry Class 11 - NEET
| 1. What is the Aufbau Principle? |  |
| 2. What is the Pauli Exclusion Principle? |  |
| 3. What is Hund's Rule of Maximum Multiplicity? |  |
| 4. How are the energies of orbitals related to the filling of orbitals? |  |
| 5. Can the energy levels of electrons in atoms change? |  |

|
Explore Courses for NEET exam
|

|


















