Atomic Spectrum & Bohr's Model of Hydrogen Atom | Chemistry Class 11 - NEET PDF Download
Electromagnetic Spectrum
The arrangement of all the electromagnetic radiation in a definite order (decreasing or increasing of wavelength or frequency is known as electro magnetic spectrum.
Spectrum
- When the light coming from a source is passed through a prism, the radiation of different wavelengths deviates through different angles and gets separated.
The angle of deviation ∝ n ∝
 Splitting of light
Splitting of light
- This process is called dispersion, and such a collection of dispersed light giving its wavelength composition is known as a spectrum.
- Spectrum is of two types:
1. Emission Spectrum
This spectrum of radiations is emitted by any source or atom or molecule of any substance (Which is excited by heating or electric discharge).
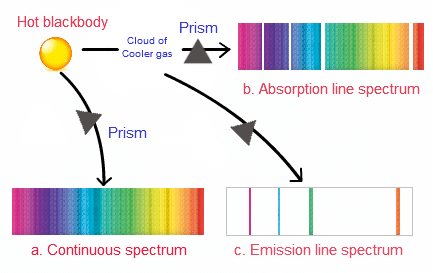
- Continuous Spectrum: When white light from a source is dispersed, a bright spectrum continuously distributed on the dark background is obtained. The colours continuously change from violet to red, and there are no sharp boundaries between various colours. These colours appear to be merged into each other, and therefore spectrum is known as a continuous spectrum.
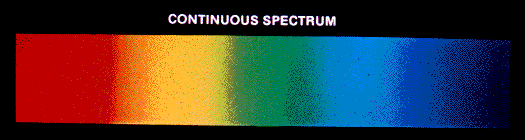
- Discontinuous Spectrum: When an atom is subjected to electromagnetic radiation, it causes excitation of an electron to higher energy level. When electrons return back to lower energy level, it emits certain radiations corresponding to the difference in energy level. Therefore, spectrum obtained in case of an atom is discontinuous. A specific wavelength is known as Atomic spectrum or line spectrum.
 Spectrum
Spectrum
2. Absorption Spectrum
- When an atom is subjected to white light it absorbs some specific radiations corresponding to the difference in energy levels, the remaining radiations (transmitted radiations) are devoid of certain specific frequencies which are observed in the form of missing line and this spectrum is known as absorption spectrum.
- It is a photographic negative of the emission spectrum, i.e. those bright lines which are present in the emission spectrum of an atom are missing.
- In the absorption spectrum and are observed in the form of dark lines.
Line Spectrum of Hydrogen Atom:
The spectrum of the H atom is observed as discontinued line spectra. The line spectra is different in 3 regions viz., UV, visible and IR. The different lines observed H spectrum were classified into different series and named after their discoverers.
Rydberg gave an empirical formula to calculate wavelength, which is applicable to all series.
RH = 109677 cm-1 Rydberg's constant.
n1 and n2 are integers.
Bohr's Model
It was the first model based on Planck's quantum theory and the model explained stability of atom and line spectrum of hydrogen.
 Bohr's Atomic Model
Bohr's Atomic Model
Postulates of Bohr's model
1. An atom consists of a centrally located small, dense, positively charged nucleus and electrons revolve around the nucleus in circular paths known as circular orbits and Coulombic force of attraction between the nucleus and the electron is balanced by the centrifugal force of the revolving electron.
2. Out of the infinite circular orbits only those circular orbits are possible in which the angular momentum of the electron is an integral multiple of h/2π i.e. angular momentum of an electron has fixed values like etc. i.e., angular momentum of the electron is quantized.
,
m and v are mass and velocities of electron respectively and r is radius of orbit and n is integer which is later related with orbit number and shell number and h is Plank's constant.
3. The energy of these circular orbits have fixed values and hence electron in an atom can have only certain values of energy. It is the characteristic of an orbit and it cannot have any orbit value of its own. And therefore energy of an electron is also quantized.
4. As long as electrons remain in these fixed orbits, it doesn't lose energy i.e. energy of an electron is stationary (not changing with time) and therefore these orbits are known as allowed energy levels or stationary states and this explains the stability of atom.
5. The energy levels are designated as K, L, M, N and numbered as 1, 2, 3, 4 etc from nucleus outwards and as the distance of the shell's or energy level from the nucleus increases the energy of the energy level also increases i.e., EN > EM > EL > Ek
6. The emission or absorption of energy in the form of radiations can only occur when an electron jump from one stationary states to other.
DE = Ehigher - Elower
DE = hn where hn is the energy of absorbed photon or emitted photon which corresponds to the difference in energy levels. Energy is absorbed when electron jumps from lower energy level (normal state) to higher energy level (exited, unstable state) and energy is emitted when electrons jumps from higher energy level to lower energy level.
Energy states in an atom.
Bohr's model is applicable for one electron species only, like H, He , Li 2+ , Be3+ etc.
Derivation of Radius of different orbits in one electron species (using Bohr's model) :
....(1)
q1 = e, q2 = Ze
=
....(2)
⇒
⇒
⇒
⇒
r = 0.529 ×
r ∝
for a particular atom r ∝ n2
Radius of 1st orbit of H atom:
r = 0.529 Å.
Ex. Calculate ratio of radius of 1st orbit of H atom to Li2+ ion :
Sol. = =
=
Derivation of Velocity of electron in Bohr's orbit :
, putting value of r.
v =
v = =
v = 2.18 × 106 m/s
v ∝
Derivation of total energy of electron / system :
T.E. of system = K.E. of e- + P.E. of system (nucleus and e-)
kinetic energy of electron = =
PE =
T.E. = - 13.6 × eV/atom
T.E. = - 2.18 × 10-18 J/atom
As shell no. or distance increases, the value of T.E. and P.E. increases (however magnitude decreases) and becomes maximum at infinity i.e., zero.
Negative sign indicates that electron is under the influence of attractive forces of nucleus.
K.E. =
T.E = - K.E.
Calculation of energy of energy levels in H atom:
(i) When n = 1 (ground level)
K.E. = 13.6 eV (atom)
P.E. = -27.2 eV / atom
T.E. = -13.6 eV/atom
(ii) When n = 2/2nd energy level / 1st excited state
K.E. = eV/atom = 3.4 eV/ atom
P.E. = - 6.8 eV/atom
T.E. = - 3.4 eV/atom
E2 - E1 = -3.4 13.6 eV/atom = 10.2 eV/atom
(iii) When n = 3 / 3rd energy level/2nd excited state.
K.E. = eV/atom = 1.51 eV/atom
P.E. = -3.02 eV/atom
T.E. = -1.51 eV/atom
-E3 - E2 = -1.51 eV/atom 3.4 eV/atom
= 1.89 eV atom.
(iv) when n = 4 / 3rd excited state
K.E. = ⇒
= 0.85 eV/atom
P.E. = -1.70 eV/atom T.E. = -0.85 eV/atom
E4 - E3 = 0.66 eV/atom.
As distance increases (n increases) energy of the energy level increases but energy difference between consecutive energy level keeps on increasing i.e., maximum energy difference between 2 to 1 (consecutive).
If reference value (P.E at ∞) is assigned value other than zero. -
(i) All K.E. data remains same.
(ii) P.E./T.E. of each shell will be changed however difference in P.E./T.E. between 2 shell will remain unchanged.
Fig: Energy levels in Hydrogen atom.
Explanation of Hydrogen spectrum using Bohr's model:
When electron in an excited atom comes back from higher energy level (n2) to lower ever level (n1) then it emits a photon, having energy equal to difference in energy levels.
hn = DE =
hn =
hn =
The theoretical value is very closed to observed value.
Bohr's model provides theoretical explanation of H spectrum.
Wavelength or wave no. of any line of any one electron species can be calculated as:
= RHZ2
,
→ nm.
Different series in the Hydrogen spectrum.
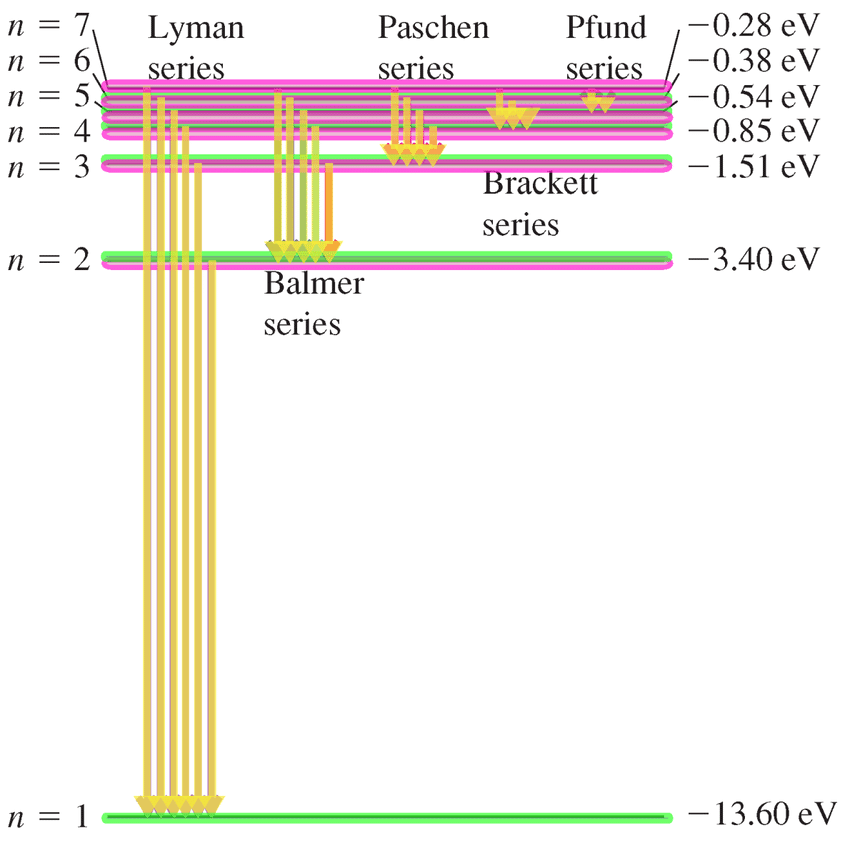 Different Series in Hydrogen Spectrum.
Different Series in Hydrogen Spectrum.
Lyman series : ni = 1, nf = 2, 3, 4, 5, - - - - - - - -
(Ultraviolet)
Balmer series : ni = 2, nf = 3, 4, 5, 6, - - - - - - - -
(Visible)
Paschen series : ni = 3, nf = 4, 5, 6, 7, - - - - - - - -
(Infrared)
Brackett series : ni = 4, nf = 5, 6, 7, - - - - - - - -
(Infrared)
Pfund series : ni = 5, nf = 6, 7, - - - - - - - -
(Infrared)
Humphrey series : ni = 6, nf = 7, 8, - - - - - - - -
(Infrared)
Ex. Calculation of different types of maximum possible radiations which can be observed in (from higher energy level to lower energy level)
Sol. n2 = n, n1 = 1
Total no. of radiation obtained having different wavelengths =
1. Transition ending at 1st level
2. Transition ending at 2nd level
3. Transition ending at (n - 1) energy levels.
= Total no. of radiation in Lymann series total no. of radiation in Balmer series .
Total no. of radiation in (n - 1) series.
= (n - 1) (n - 2) (n - 3) ........................ 2 1
⇒ ⇒
⇒ ............................ 2 1
Total no. of different radiations:
=
N = difference in higher energy level and lower energy level.
Ex. The energy level of an atom for 1st, 2nd and third levels are E, 4E, 2E respectively. If a photon of wavelength l is emitted for a transition 3 to 1. Calculate the wavelength for transition 2 to 1 in terms of l.
Sol. 2E - E = E = ⇒ 3l = l2
Ex. Let n1 be the frequency of the series limit of the Lyman series, n2 be the frequency of 1st line of the Lyman series, and n3 be the frequency of the series limit of the Balmer series. Then find relation between n1, n2 and n3
Sol.
E1 = E2 E3
⇒ ⇒ n1 = n2 n3
Ex. Hydrogen-like species is observed to emit 6 wavelengths originating from all possible transitions between a group of levels these energy levels have energy between - 0.85 eV and -0.544 eV (including both these energy levels) calculate
(i) The quantum number of levels between which transition is taking place.
(ii) Find the atomic number of species.
Sol. (n2 - n1) (n2 - n1 1) = 12
n2 - n1 = x x(x 1) = 12
n2 = n1 3
n1 = 12 ; n2 = 15
Failures of Bohr's Model
(i) It is applicable only for one-electron species.
(ii) He couldn't explain the fine spectrum of hydrogen when a powerful spectroscope is used then several lines which are very closely placed are observed in addition to the expected lines later this problem was solved by Sommerfeld who introduced the concept of the subshell.
(iii) He couldn't explain the splitting of spectral lines into a group of finer lines under the influence of an external magnetic field (Zeeman effect) or under the influence of an external electric field (stark effect).
(iv) He couldn't give a theoretical reason for most of his assumptions, for example, he couldn't justify why the angular momentum of the electron should be quantised.
(v) The Spectrum of isotopes of hydrogen was expected to be the same according to Bohr's model but was found different experimentally.
Sommerfeld model of Atom
Three refinements of the Bohr model were worked out by Arnold Sommerfeld and are jointly responsible for giving rise to small deviations in the allowed energies from the values En These refinements brought the calculated frequencies into even better agreement with observation (from four to five significant digits). The refinements were:
(a) the introduction of elliptical orbits;
(b) allowance for an orbiting motion of the nucleus; and
(c) the consideration of relativistic mass effects.
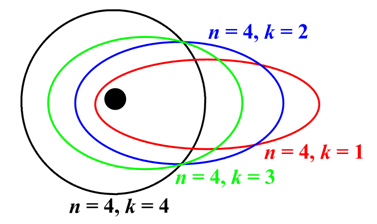 Fig: Sommerfeld model of Atom.
Fig: Sommerfeld model of Atom.
|
114 videos|263 docs|74 tests
|
FAQs on Atomic Spectrum & Bohr's Model of Hydrogen Atom - Chemistry Class 11 - NEET
| 1. What is the electromagnetic spectrum? |  |
| 2. What is Bohr's model of the atom? |  |
| 3. What is the Sommerfeld model of the atom? |  |
| 4. What is an atomic spectrum? |  |
| 5. How does Bohr's model explain the hydrogen atom spectrum? |  |

















