Buckingham's Pie Theorem | Civil Engineering Optional Notes for UPSC PDF Download
Buckingham Pi Theorem Meaning: A Basic Overview
The Buckingham Pi theorem is a principle used in dimensional analysis to ensure that a mathematical expression is dimensionally homogenous. This essentially means that all elements of an equation have the same measurement units.Dimensional homogeneity: An equation is dimensionally homogenous if all of its terms have the same dimensions or units of measurement. For example, adding metres to metres or seconds to seconds, etc.
In physical systems, there are often fewer independent variables than would appear from the basic physical dimensions. The Buckingham Pi theorem provides a means for finding combinations of these physical variables that form dimensionless parameters, or The Buckingham Π terms. These dimensionless parameters can then be used to express the behaviour of the system in a more simplified and manageable way.
Detailed Explanation of Buckingham Pi Theorem Meaning
The Buckingham Pi theorem is all about identifying relationships between variables in physical systems. The theorem enables us to reduce the number of variables in an equation by transforming it into a set of dimensionless parameters. Let's start with its mathematical representation. For a system with N variables x
The Mathematical Approach to Buckingham Pi Theorem
Getting involved in the mathematics behind the Buckingham Pi theorem allows a deeper understanding of how it functions and its practical applications. It essentially provides a systematic method for computing sets of dimensionless parameters from certain given variables.The Buckingham Pi Theorem Formula: An Explanation
To comprehend the Bucking Pi theorem deeply, you need to understand both its formulation and the concepts that underpin it. The equation to remember for the Buckingham Pi theorem is:
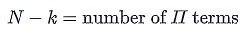
Here,
- Selecting k variables from the total N variables that encompass all the fundamental dimensions of the problem.
- The remaining N - k variables are then chosen. Each of these is combined with the previously chosen variables to create dimensionless Π - terms.
Working Through Buckingham Pi Theorem Formula Step by Step
Let's now delve into the step-by-step application of the Buckingham Pi theorem.- Step 1: Identify the relevant variables which affect the physical phenomenon, and note down their fundamental dimensions.
- Step 2: Count the number of variables (N) and the number of fundamental dimensions they encompass (k).
- Step 3: The difference between number of variables and fundamental dimensions (N - k) will give you the count of Π-terms.
- Step 4: Choose k variables which contain all the fundamental dimensions in them.
- Step 5: Use these k variables and remaining variables in system to construct Π-terms using dimensional homogeneity.
Buckingham Pi Theorem Examples: Putting Theory into Practice
Let's put the theory into practice with a hypothetical problem in fluid mechanics, where the pressure drop across an orifice plate is dependent on the diameter of the orifice, density and velocity of the fluid, and the viscosity of the fluid. The relevant variables and their dimensions can be tabulated as: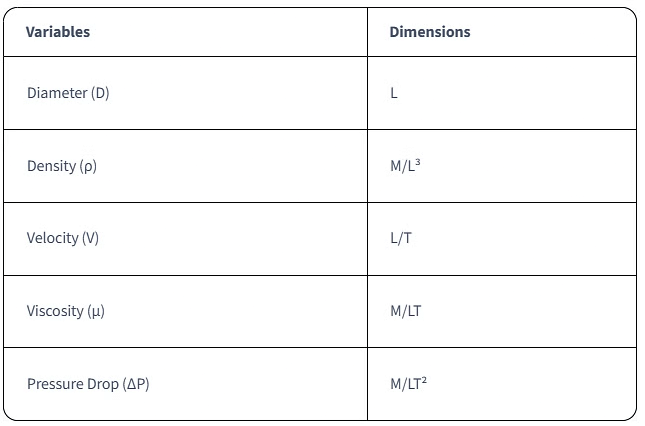
Buckingham Pi Theorem Fluid Mechanics: A Key Application
Fluid mechanics, the study of how fluids (liquids, gases, and plasmas) behave under various forces and in different conditions, employs the Buckingham Pi theorem extensively. It's pivotal for dealing with complex parameters in fluid dynamics and assists in identifying reduced independent variables. Scientists too often find themselves dealing with intertwined physical quantities, making direct analysis problematic. Here's where the Buckingham Pi theorem proves immensely valuable. Through the theorem, measurable physical entities such as pressure, velocity, density, and viscosity are transformed into dimensionless Pi terms. These Pi terms encapsulate the relevant relationships between the primary variables without the constraint of physical dimensions. This makes cyclic procedures manageable, provides clearer insights, and helps in setting up experiments efficiently, as you can vary one parameter at a time.Understanding Buckingham Pi Theorem Fluid Mechanics with Examples
To see how the Buckingham Pi theorem is applied in fluid mechanics, consider the problem of predicting the pressure drop across a pipe due to fluid flow. Take into account variables like pipe diameter (D), fluid density (ρ), velocity (V), and viscosity (
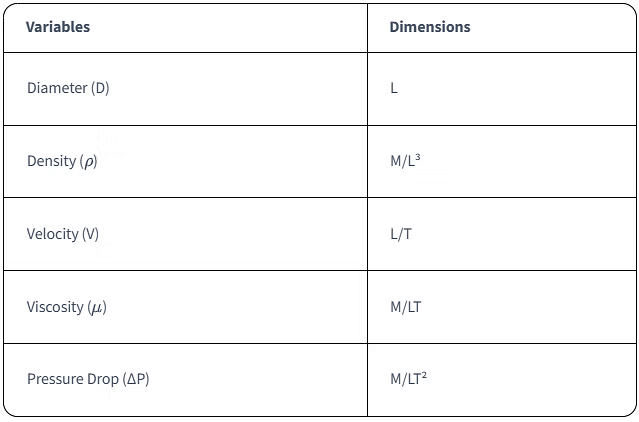
By applying the Buckingham Pi theorem, you get dimensionless quantities such as the Reynolds number, which aids in identifying the flow regime (laminar, transitional, or turbulent). The theorem allows you to simplify the complex relationships between the factors affecting pressure drop, making the task of understanding and predicting the behaviour of fluid flow easier.
Other Significant Applications of Buckingham Pi Theorem
Although the Buckingham Pi theorem is extensively used in fluid mechanics, it's application covers a broader spectrum, reaching out to various scientific and engineering disciplines. For instance, in aerospace engineering, the theorem helps predict the performance of jet engines by forming dimensionless parameters from several factors, including ambient temperature, fuel-air ratio, engine speed, etc. In physics, it simplifies complex problems by reducing the number of independent variables in equations. The theorem holds significant practical value, given its capacity to make the representation of physical systems concise and manageable.
Engineering Applications of Buckingham Pi Theorem
In the vast expanse of engineering, the Buckingham Pi theorem is applied across diverse specialities, including electrical, mechanical, civil, chemical, and aerospace engineering. For instance, in mechanical engineering, the theorem is engaged to resolve issues with machine kinematics, fluid motion, and heat transfer. Civil engineers leverage it to understand soil mechanics, structural dynamics, and fluid flows while chemical engineers employ it to decipher reactor design, mass transfer, and fluid dynamics. In each of these examples, the theorem serves to simplify extensive, detailed physical phenomena, making them understandable and effectively manageable.
Practical Buckingham Pi Theorem Examples in Real Life
It's crucial to appreciate that the value of Buckingham Pi theorem extends beyond complex scientific or engineering scenarios to well-known real-life phenomena. For instance, consider the task of flying a kite. Here, the parameters at play include the kite's mass, surface area, string length, wind speed, angle of elevation, and gravity. These multiple physical quantities make the analysis complex. However, by applying the Buckingham Pi theorem, these variables can be converted into a simpler set of dimensionless parameters, thereby simplifying the problem and easing the analysis. Thus, the theorem has an extensive range in terms of application, covering the needs of both complicated aerospace operations and as commonplace as flying a kite.
Step by Step Approach to Buckingham Pi Theorem Dimensional Analysis
Conducting a dimensional analysis using the Buckingham Pi theorem involves a process that can be broken down as follows:
- Step 1: Identify the relevant variables associated with the physical phenomenon.
- Step 2: Define the physical dimensions of these variables. It's essential to ensure you cover all possible dimensions throughout the process.
- Step 3: Determine the number of variables and fundamental dimensions. Use these values in the Buckingham Pi theorem to calculate the number of non-dimensional Π-terms:

- Step 4: Select the repeating variables from the list of parameters. These repeating variables must, when multiplied or divided, represent all fundamental dimensions.
- Step 5: Formulate non-dimensional Π-terms from the repeating and non-repeating variables, making sure each term is dimensionally homogeneous.
These steps might seem complex at first, but with some meticulous practice, the Buckingham Pi theorem can become a handy tool for performing dimensional analyses.
Using Buckingham Pi Theorem Dimensional Analysis in Engineering Scenarios
Whether it's aerospace, mechanical or electrical engineering, the Buckingham Pi theorem finds multiple applications in these domains. In mechanical engineering, take for example, the performance of a centrifugal pump which depends on several factors like rotational speed, impeller diameter, fluid density, fluid viscosity and gravitational acceleration. Through the Buckingham Pi theorem, you can convert these factors into non-dimensional parameters like Reynolds number, Froude number and Euler number, which are fundamental in understanding and predicting the pump’s behaviour. In civil engineering, the theorem is used in studying the movement of a particle in fluid - where parameters like fluid speed, particle size, particle density, fluid density and fluid viscosity all play a part. Dimensional analysis helps derive the influential non-dimensional Drag coefficient, Shields parameter etc., that simplify the study. Similarly, in electrical engineering, the theorem plays role in analysing complex circuits and networks by reducing variables to dimensionless groups. All these applications revolve around using similar step-by-step methodology discussed above. By simplifying problems into digestible terms, the Buckingham Pi theorem makes engineering designs and developments more efficient and manageable. Hence, tuning your dimensional analytical skills using Buckingham Pi theorem could be beneficial in cracking various engineering scenarios.Exploring Further: Buckingham Pi Theorem Applications
While the mention of the Buckingham Pi theorem might seem daunting, when broken down into its basic principles and purpose, its application in various sectors is nothing short of impressive. The understanding of this theorem goes a long way towards simplifying multifaceted problems, illustrating the relationships between multiple parameters, and helping to design experiments or models effectively.
The Buckingham Pi theorem, due to its radical dimensional simplification, has earned a place as a standard tool in the scientific and engineering fields.
Advanced Usage and Interpretation of Buckingham Pi Theorem
Applying the Buckingham Pi theorem isn't just about deriving non-dimensional parameters, instead its broader scope involves utilising these derivations to extract valuable and advanced insights. Let's take a more carefully calculated look:
- Variable Reduction: By converting the original set of variables into Pi terms, the Buckingham Pi theorem drastically reduces the number of variables that need to be studied or experimented upon.
- Data Correlation: Once non-dimensional parameters are established, they can be used as a tool for correlating experimental and computed data more efficiently.
- Data Extrapolation: Utilising these Pi terms also aids in data extrapolation, making predictions outside existing datasets.
- Theoretical Analysis: The theorem assists in theoretical analysis by simplifying multi-parameter problems into single-parameter equations.
Buckingham Pi theorem, therefore, serves as a vital tool enabling advanced variable reduction, data correlation, extrapolation and theoretical analysis in many scientific and engineering problems.
Critiques and Limitations of Buckingham Pi Theorem
Like every scientific principle, Buckingham Pi theorem isn't entirely flawless. Some criticisms and limitations pertaining to the theorem need careful consideration. Here are some of them:
- Lack of Uniqueness: One of the theorem's main limitations is the lack of uniqueness in the Pi terms. The theorem may produce multiple Pi terms for the same system, depending on the choice of repeating variables.
- Interpretation Challenges: Understanding and interpreting the physical or practical significance of the derived Pi terms can sometimes be challenging.
- Unsuitability for Dimensionless Problems: The theorem is not effective for problems where all variables are dimensionless (scaling problems).
- It Does Not Provide Causality: The method identifies what parameters are critical, but it does not identify how these parameters interact or affect each other.
Despite these limitations and critiques, the Buckingham Pi theorem remains a valuable dimensionless analysis approach. But for its effective utilization, bearing these limitations in mind is key to gaining accurate and insightful understanding of complex physical scenarios.
|
350 videos|464 docs|2 tests
|
FAQs on Buckingham's Pie Theorem - Civil Engineering Optional Notes for UPSC
| 1. What is the Buckingham Pi Theorem and its significance in fluid mechanics? |  |
| 2. How is the Buckingham Pi Theorem applied in advanced settings beyond fluid mechanics? |  |
| 3. Can you explain the mathematical approach involved in the Buckingham Pi Theorem? |  |
| 4. What are some common examples where the Buckingham Pi Theorem is used in practical engineering applications? |  |
| 5. How can one interpret the results obtained using the Buckingham Pi Theorem in real-world engineering scenarios? |  |
|
350 videos|464 docs|2 tests
|

|
Explore Courses for UPSC exam
|

|

















