Case Based Questions: Coordinate Geometry | Mathematics (Maths) Class 10 PDF Download
Q1: Read the source below and answer the questions that follow:
Jagdish has a Field which is in the shape of a right angled triangle AQC. He wants to leave a space in the form of a square PQRS inside the field for growing wheat and the remaining for growing vegetables (as shown in the figure). In the field, there is a pole marked as O.
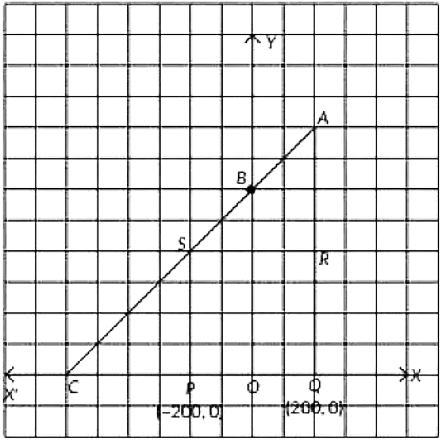
i. Taking O as origin, coordinates of P are (-200, 0) and of Q are (200, 0). PQRS being a square, what are the coordinates of R and S?
(1 mark)
ii. What is the area of square PQRS? (1 mark)
iii. What is the length of diagonal PR in square PQRS? (1 mark)
iv. If S divides CA in the ratio K: 1, what is the value of K, where point A is (1 mark)
Ans:
i. We have. P = (-200, 0) and Q = (200, 0)
The coordinates of R and S are (200, 400) and (-200, 400).
ii. The length PQ = 200 + 200 = 400 units.
Area of square PQRS = 400 x 400 = 160000 sq. units.
iii. Length of diagonal PR = √2 x length of side = 400√2 units.
iv. Here,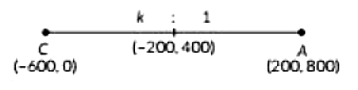
Using section formula, we have
∴ (Kx₂ + x₁) / (K + 1) , (Ky₂ + y₁) / (K + 1) = (-200, 400)
⇒ (K(200) + (-600)) / (K + 1) , (K(800) + 0) / (K + 1) = (-200, 400)
⇒ (200K - 600) / (K + 1) , (800K) / (K + 1) = (-200, 400)
∴ (800K) / (K + 1) = 400
⇒ 800K = 400K + 400
⇒ 400K = 400
⇒ K = 1
Q2: Read the source below and answer the questions that follow:
Alia and Shagun are friends living on the same street in Patel Nagar. Shagun's house is at the intersection of one street with another street on which there is a library. They both study in the same school and that is not far from Shagun's house. Suppose the school is situated at the point O, i.e., the origin, Alia's house is at A. Shagun's house is at B and library is at C.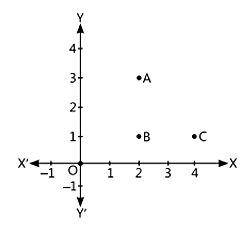
i. How far is Alia's house from Shagun's house? (1 mark)
ii. How far is the library from Shagun's house? (1 mark)
iii. Show that for Shagun, school is farther compared to Alia's house and library. (1 mark)
iv. Show that Alia's house, Shagun's house and library for an isosceles right triangle. (1 mark)
Ans:
i. The coordinates of Alia's house and Shagun's house are A (2, 3) and B (2, 1) respectively.
∴ Distance of Alia's house from Shagun's house is,
BA = √((2 - 2)² + (3 - 1)²)
= √(0)² + (2)²
= √0 + 4 = 2 units.
ii. The coordinates of Shagun's house and library are
B (2, 1) and (4, 1) respectively.
Distance of library from Shagun's house is,
BC = √((4 - 2)² + (1 - 1)²)
= √(2)² + (0)²
= √4 + 0 = 2 units.
iii. The coordinates of school, Alia's house, Shagun's house and library are O(0, 0), A (2, 3), B (2, 1) and C (4,1).
Now, BA = √((2 - 2)² + (3 - 1)²) = √(0)² + (2)²
= √0 + 4 = 2 units.
BC = √((4 - 2)² + (1 - 1)²) = √(2)² + (0)²
= √4 + 0 = 2 units.
and BO = √((0 - 2)² + (0 - 1)²) = √(-2)² + (-1)²
= √4 + 1 = √5 units.
Here, BO is greater than BA and BC.
For Shagun, School (0) is farther than Alia's house (A)
and library (C).
Hence proved.
iv. The coordinates of Alia's house, Shagun's house and library are A (2, 3), B (2, 1) and C (4, 1) respectively using distance formula,
AB = √((2 - 2)² + (1 - 3)²) = √(0)² + (-2)²
= √0 + 4 = 2 units.
BC = √((4 - 2)² + (1 - 1)²) = √(2)² + (0)²
= √4 + 0 = 2 units.
and CA = √((2 - 4)² + (3 - 1)²) = √(-2)² + (2)²
= √4 + 4 = √8 = 2√2 units.
Here, AB² + BC² = (2)² + (2)² = 4 + 4 = 8 = CA² and AB = BC..
Therefore, A, B and C form an isosceles right triangle.
Hence proved.
Q3: Read the source below and answer the questions that follow:
All of the persons know that smoking is injurious to health. So, some college students decided to start a campaign. To raise social awareness about hazards of smoking, they started "NO SMOKING" campaign. Some students were asked to prepare campaign banners in the shape of triangle which is as shown in the figure:
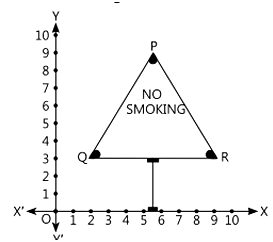 i. Find the coordinates of the mid-point of Q and R. (1 mark)
i. Find the coordinates of the mid-point of Q and R. (1 mark)ii. Find the area of the triangle PQR. (1 mark)
iii. Find the point on X-axis, which is equidistant from points Q and R. (1 mark)
iv. Find the centroid of the triangle PQR. (1 mark)
Ans:
i. The coordinates of the vertices of Q and R are (2, 3) and (9,3) respectively.
∴ Mid-point of Q and R = ((2 + 9) / 2 , (3 + 3) / 2)
= (11 / 2 , 3)
ii. The coordinates of the vertices of P, Q and R are (6, 9), (2, 3) and (9, 3) respectively.
Now, base of the ΔPQR = QR = √((9 - 2)² + (3 - 3)²)
= √(49 + 0) = 7 units.
and height of the ΔPQR = Perpendicular distance
from the vertex P to the base QR = (9 - 3) = 6 units.
∴ Area of ΔPQR = 1/2 × base × height
= 1/2 × 7 × 6 = 21 sq. units.
iii. Let point on X-axis be P(x, 0)
Then (QP)² = (PR)²
(x - 2)² + (0 - 3)² = (9 - x)² + (3 - 0)²
= x² - 4x + 4 + 9 = 81 - 18x + x² + 9
14x = 77
⇒ x = 11 / 2
∴ Point on X-axis is (11 / 2 , 0)
iv. ∴ Centroid of the ΔPQR = ((6 + 2 + 9) / 3 , (9 + 3 + 3) / 3)
= (17 / 3 , 15 / 3)
= (17 / 3 , 5)
Q4: Read the source below and answer the questions that follow:
On Annual Sports Day of a school, parallel lines have been drawn with lime powder at a distance of 1 m from each other in a rectangular shaped school playground. 80 plastic cones have been placed at a distance of 1 m from each other along PY as shown in figure. Pushpendra runs (1/4)th the distance PY on the 3rd line and posts a yellow flag. Pankaj runs (1/5)th the distance PY of the 7th line and posts a blue flag.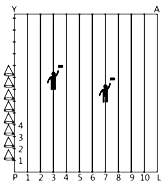
i. Find the coordinates of the yellow flag. (1 mark)
ii. What is the distance between both the flags? (1 mark)
iii. If Raman has to post a green flag exactly halfway between the line segment joining the two flags, where should he post his flag?
(1 mark)
iv. If Raman change his position and post a green flag at a point between the line segment joining the two flags, then find the coordinate of the green flag which divides the line segment internally in the ratio 1 : 2. (1 mark)
Ans:
i. (1/4)th the distance PY = 80 / 4 m = 20 m
∴ Coordinates of yellow flag = (3, 20)
ii. (1/5)th the distance PY = 80 / 5 m = 16 m
∴ Coordinates of blue flag = (7, 16)
Distance between both flags
= √((7 - 3)² + (16 - 20)²)
= √(4)² + (-4)²
= √16 + 16 = √32 = 4√2 m
iii. Position of green flag = Mid-point of yellow and blue flag
= ((3 + 7) / 2 , (20 + 16) / 2)
= (10 / 2 , 36 / 2)= (5, 18)
Hence, Raman should post his green flag at 18 m on 5th line.
iv. Given points: (3, 20) and (7, 16)
Here, x₁ = 3, y₁ = 20, x₂ = 7, y₂ = 16
and ratio m₁ : m₂ = 1 : 2
Let the point of division be P(x, y):
Then from division formula:
x = (m₁x₂ + m₂x₁) / (m₁ + m₂) and y = (m₁y₂ + m₂y₁) / (m₁ + m₂)
= (1 × 7 + 2 × 3) / (1 + 2) = 13 / 3
and y = (1 × 16 + 2 × 20) / (1 + 2) = 56 / 3
Therefore, the coordinate of the green flag is (13 / 3 , 56 / 3).
|
127 videos|584 docs|79 tests
|





















