Case Based Questions: Introduction to Trigonometry | Mathematics (Maths) Class 10 PDF Download

Q1: Read the source below and answer the questions that follow:

In structural design, a structure is composed of triangles that are interconnecting. A truss a series of triangle in same plane end is one of the major types of engineering structures and is especially used in the design of bridges and buildings. Trusses are designed to support loads, such as the weight of people. A truss is exclusively made of long, straight members connected by joints at the end of each member.
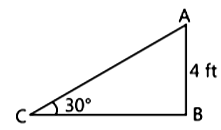This is a single repeating triangle in a truss system.

i. In the above triangle, what is the length of AC? (1 mark)
ii. In the above triangle, what is the length of BC? (1 mark)
iii. If sin A = sin C, what will be the length of BC? (1 mark)
iv. If the length of AB doubles, what will happen the Length of AC? Solutions (1 mark)

Ans:
i. In right-angled ΔABC,
sin 30° = AB / AC  ⇒  1 / 2 = 4 / AC
⇒  AC = 8 ft
ii. In right-angled ΔABC,
tan 30° = AB / BC  ⇒  1 / √3 = 4 / BC
⇒  BC = 4√3 ft
iii. Given,   sin A = sin C
In right-angled ΔABC,
BC / AC = AB / AC  ⇒  BC = AB = 4 ft
iv. Given, AB = 2 × 4 = 8 ft
∴ In right ΔABC, sin 30° = AB / AC
⇒  1 / 2 = 8 / AC
⇒  AC = 16 ft
So, AC doubles the original length.

Q2: Read the source below and answer the questions that follow:

Soniya and her father went to her friend Ruhi to enjoy party. When they reached Ruhi's place, Soniya saw the roof of the house, which was triangular in shape. She imagined the dimensions of the roof which is as given in the figure.

i. If D is the mid-point of AC, then find BD. (1 mark)
ii. Find the measure of <A and <C. (1 mark)
iii. Find the value of sin A + cos C. (1 mark)
iv. Find the value of tan² C + tan² A. (1 mark)

Ans:
i. We have, AB = BC = 6√2 m and AC = 12 m
D is the mid-point of AC.
∴ AD = DC = 12 / 2 = 6 m
In right-angled ΔADB, use Pythagoras theorem
AB² = BD² + AD²
⇒  BD² = (6√2)² - 6²
⇒  BD² = 72 - 36 = 36
⇒  BD = 6 m
ii. In right ΔADB, sin A = BD / AB = 6 / 6√2 = 1 / √2  (from part (1))
⇒  sin A = sin 45°  ⇒  ∠A = 45°
In right ΔBDC, tan C = BD / DC = 6 / 6
⇒  tan C = 1 = tan 45°  ⇒  ∠C = 45°
iii. Here, sin A = 1 / √2  and cos C = cos 45° = 1 / √2
∴ sin A + cos C = (1 / √2) + (1 / √2) = 2 / √2 = √2
iv. Here, tan C = 1 and tan A = tan 45° = 1
⇒  tan² C + tan² A = 1 + 1 = 2

Q3: Read the source below and answer the questions that follow:

Three friends-Sanjeev, Amit and Digvijay are playing hide and seek in a park. Sanjeev and Amit were supposed to hide and Digvijay had to find both of them. If the positions of three friends are at A, B and C respectively as shown in the figure and forms a rightangled triangle such that AB = 9 m, BC= 3√3 m and B = 90°.

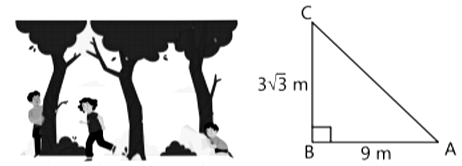
i. Find the measure of <A by using trigonometric ratio. (1 mark)
ii. Find the measure of <C by using trigonometric ratio. (1 mark)
iii. Find the length of AC. (1 mark)
iv. Find the value of cos 2A. (1 mark)
Or
iv. Find the value of sin(C / 2). (1 mark)

Ans:
i. We have, AB = 9 m, BC = 3√3 m
In right ΔABC, we have
tan A = BC / AB = (3√3) / 9 = 1 / √3
⇒  tan A = tan 30°  ⇒  ∠A = 30°
ii. In right ΔABC,
We have, tan C = AB / BC = 9 / 3√3 = √3
⇒  tan C = tan 60°  ⇒  ∠C = 60°
iii. In right ΔABC, sin A = BC / AC
⇒  sin 30° = BC / AC  (from part (1))
⇒  1 / 2 = (3√3) / AC  ⇒  AC = 6√3 m
iv. ∴ ∠A = 30°  (from part (1))
Or
∴ cos 2A = cos (2 × 30°) = cos 60° = 1 / 2
iv. ∴ ∠C = 60°
∴ sin (C / 2) = sin (60° / 2) = sin 30° = 1 / 2