Case Based Questions: Quadratic Equations | Mathematics (Maths) Class 10 PDF Download

Q1: Read the source below and answer the questions that follow:

Chenab railway bridge is the World's tallest railway bridge in Jammu and Kashmir Territory, which is constructed on Chenab river. Its shape is a parabolic arch, whose equation is in the form of ax² + bx + c = 0. The nature of roots can be defined as: 
(i) D=b2-4ac > 0, roots are real and distinct. 
(ii) D=b2-4ac = 0, roots are real and equal. 
(iii) D=b2-4ac < 0, roots are imaginary. 

i. Find the nature of roots of the equation 5x²-4x-3=0. (1 mark)
ii. Identify the type of the roots of quadratic equation x²+3x+3=0. (1 mark)
iii. Find the value of k in which the equation 3x² - 2x + 4k = 0 has equal roots. (1 mark)
iv. Find the value of k for which the equation x²+5kx+16=0 has no real root. (1 mark)

Ans:
i. Given equation is 5x²-4x-3=0.  
On comparing with ax2 + bx + c = 0, we get a=5, b = -4 and c=-3 
Now, discriminant D=b2-4ac =(-4)2-4x5x (-3) = 16+6076 > 0 
Hence, roots of given equation are real and distinct.
ii. Given quadratic equation is x²+3x+3=0. 
On comparing with ax² + bx + c = 0, we get a=1, b 3 and c=3 .. 
Discriminant, D=b2-4ac = (3)² - 4x1x3 =9-12=-3<0 
Hence, roots of given equation are imaginary.
iii. Given quadratic equation is 3x²-2x+4k=0. 
On comparing with ax² + bx + c = 0, we get a=3, b=-2 and c = 4k 
As the roots of the given equation are equal. 
Therefore, discriminant D= b2-4ac=0 
= (-2)²-4 × 3 × 4k = 0 
= 4-4 x 12k = 0 
= 1-12k=0
k = 1/12
iv. Given equation: x² + 5kx + 16 = 0
Comparing this equation with general quadratic equation 
ax² + bx + c = 0 a = 1, b = 5k and c = 16 .. 
Discriminant (D)= b² - 4ac = (5k²)-4(1) (16)
= 25k² - 64
If the given equation has no real root, then
D < 0
⇒ 25k² - 64 < 0 ⇒ k² < 64/25
⇒ k² - (8/2)² < 0
⇒ -8/5 < k < 8/5 (∵ x² - a² < 0 ⇒ -a < x < a)
Therefore, the roots of the given equation will not be real if -8/5 < k < 8/5.

Q2: Read the source below and answer the questions that follow:

In the picture given below, one can see a rectangular in-ground swimming pool installed by a family in their backyard. There is a concrete sidewalk around the pool of width x m. The outside edges of the sidewalk measure 7 m and 12 m. The area of the pool is 36 sq. m.
i. Write the representation of the length and breadth of the pool algebraically. (1 mark)
ii. Form a quadratic equation in terms of x. (1 mark)
iii. Find the length of the sidewalk around the pool. (1 mark)
iv. Find the width of the sidewalk around the pool. (1 mark)

Ans:
i. Given, width of the path be x metres. Inside, length and breadth of a rectangular pool are L= (12-2x) m and b = (7-2x)m.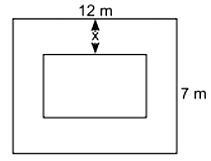
ii. Area of the pool = lx b 
= (12-2x) x (7-2x) 
=84 - 24x - 14x + 4x² 
=4x² - 38 x + 84 .. 
The required quadratic equation in terms of x is 
4x² - 38x + 84 - 0 
or 2x² - 19x + 42 = 0 
iii. We have, area of the pool is 36 m². 
:- 4x²- 38x + 84 = 36 
= 2x²-19x + 4218 
= 2x²-19x + 24 = 0 
= 2x² - (16 + 3)x + 24 = 0 
= 2x²- 16x - 3x + 24 = 0 
= 2x (x - 8) -3(x - 8) = 0 
= (2x - 3) (x - 8) = 0
x = 3/2, x = 8
⇒ When x = 8,
b = 7 - 2 × 8
= -9 which is not possible
So, we neglect x = 8.
Consider, x = 3/2.
∴ Length
l = 12 - 2 × 3/2 = 9 m
So, length of the sidewalk around the pool is 9m.
iv. ∴ Width
b = 7 - 2 × 3/2 = 4 m.
So, width of the sidewalk around the pool is 3/2 m.

Q3: Read the source below and answer the questions that follow:

i. Find the nature of roots of the equation 4x² - 7x + 3 = 0. (1 mark)
ii. Identify the type of the roots of the quadratic equation x² - 4x + 5 = 0. (1 mark)
iii. Find the value of k for which the equation 2x² - kx + 8 = 0 has equal roots. (1 mark)
iv. Find the value of k for which the equation x² - 6kx + 9 = 0 has no real root. (1 mark)

Ans:
i. Given equation is 4x² - 7x + 3 = 0.
On comparing with ax² + bx + c = 0, we get a = 4, b = -7, and c = 3.
Now, discriminant D = b² - 4ac = (-7)² - 4 × 4 × 3 = 49 - 48 = 1 > 0
Hence, the roots of the given equation are real and distinct.
ii. Given quadratic equation is x² - 4x + 5 = 0.
On comparing with ax² + bx + c = 0, we get a = 1, b = -4, and c = 5.
Discriminant, D = b² - 4ac = (-4)² - 4 × 1 × 5 = 16 - 20 = -4 < 0
Hence, the roots of the given equation are imaginary.
iii. Given quadratic equation is 2x² - kx + 8 = 0.
On comparing with ax² + bx + c = 0, we get a = 2, b = -k, and c = 8.
As the roots of the given equation are equal,
Discriminant D = b² - 4ac = 0
= (-k)² - 4 × 2 × 8 = 0
= k² - 64 = 0
k² = 64
k = ±8
iv. Given equation: x² - 6kx + 9 = 0
Comparing this equation with the general quadratic equation ax² + bx + c = 0, we get a = 1, b = -6k, and c = 9.
Discriminant (D) = b² - 4ac = (-6k)² - 4(1)(9)
= 36k² - 36
For no real roots, D < 0
⇒ 36k² - 36 < 0 ⇒ k² < 1
⇒ -1 < k < 1
Therefore, the roots of the given equation will not be real if -1 < k < 1.

Q4: Read the source below and answer the questions that follow:

i. Find the nature of roots of the equation 3x² - 5x + 2 = 0. (1 mark)
ii. Identify the type of the roots of the quadratic equation x² + 6x + 10 = 0. (1 mark)
iii. Find the value of k for which the equation 5x² - kx + 9 = 0 has equal roots. (1 mark)
iv. Find the value of k for which the equation x² - 8kx + 16 = 0 has no real root. (1 mark)

Ans:
i. Given equation is 3x² - 5x + 2 = 0.
On comparing with ax² + bx + c = 0, we get a = 3, b = -5, and c = 2.
Now, discriminant D = b² - 4ac = (-5)² - 4 × 3 × 2 = 25 - 24 = 1 > 0
Hence, the roots of the given equation are real and distinct.
ii. Given quadratic equation is x² + 6x + 10 = 0.
On comparing with ax² + bx + c = 0, we get a = 1, b = 6, and c = 10.
Discriminant, D = b² - 4ac = (6)² - 4 × 1 × 10 = 36 - 40 = -4 < 0
Hence, the roots of the given equation are imaginary.
iii. Given quadratic equation is 5x² - kx + 9 = 0.
On comparing with ax² + bx + c = 0, we get a = 5, b = -k, and c = 9.
As the roots of the given equation are equal,
Discriminant D = b² - 4ac = 0
= (-k)² - 4 × 5 × 9 = 0
= k² - 180 = 0
k² = 180
k = ±√180 = ±6√5
iv. Given equation: x² - 8kx + 16 = 0
Comparing this equation with the general quadratic equation ax² + bx + c = 0, we get a = 1, b = -8k, and c = 16.
Discriminant (D) = b² - 4ac = (-8k)² - 4(1)(16)
= 64k² - 64
For no real roots, D < 0
⇒ 64k² - 64 < 0 ⇒ k² < 1
⇒ -1 < k < 1
Therefore, the roots of the given equation will not be real if -1 < k < 1.

Q4: Read the source below and answer the questions that follow:

i. Assuming the original length of each side of a tile is x units, make a quadratic equation from the above information. (1 mark)
ii. Write the corresponding quadratic equation in standard form. (1 mark)
iii. (a) Find the value of x, the length of the side of a tile by factorisation. (2 marks)
OR
iii. (b) Solve the quadratic equation for x using the quadratic formula. (2 marks)

Ans:
i. Let the original side length of each tile be x units.
The area of the rectangular floor using 200 tiles = 200 x2 unit2 
The area with increased side length (each side increased by 1 unit) using 128 tiles
= 128 (x + 1)2 unit2
So, the required quadratic equation is: 200x2 = 128 (x + 1 )2
ii. We have,
200 x 2 = 128 (x + 1)2
⇒ 200 x 2 = 128 (x2 + 2x + 1)
⇒ 200 x 2 = 128x2 + 256x + 128
⇒ 72x2 − 256x − 128 = 0
which is the quadratic equation is standard form.
iii. (a) We have,
72x2 − 256x − 128 = 0
or, 9x2 − 32x − 16 = 0
or, 9x2 − 36x + 4x − 16 = 0
or, 9x (x − 4) + 4 (x − 4) = 0
or, (x − 4) (9x + 4) = 0
or, x = 4, - 4/9
Since the side cannot be negative, thus x = 4 units.
OR
(b) We have 9x2 − 32x − 16 = 0
On comparing with ax2 + bx + c = 0, we get
a = 9, b = −32 and c = −16
Using quadratic formula,
x = (-b ± √(b² - 4ac)) / (2a)
x = (-(-32) ± √((-32)² - 4(9)(-16))) / (2 × 9)
x = (32 ± √(1024 + 576)) / 18
x = (32 ± √1600) / 18
x = (32 ± 40) / 18
x = (32 + 40) / 18  or  (32 - 40) / 18
x = 72 / 18  or  -8 / 18
x = 4  or  -4/9