Cell Potential Under Nonstandard Conditions | Chemistry Optional Notes for UPSC PDF Download
Introduction
The Nernst Equation enables the determination of cell potential under non-standard conditions. It relates the measured cell potential to the reaction quotient and allows the accurate determination of equilibrium constants (including solubility constants).
The Effect of Concentration on Cell Potential: The Nernst Equation
Recall that the actual free-energy change for a reaction under nonstandard conditions, ΔG, is given as follows:
We also know that ΔG = −nFEcell (under non-standard conditions) and ΔGo = −nFEocell (under standard conditions). Substituting these expressions into Equation 20.6.1, we obtain
Dividing both sides of this equation by −nF,
Equation 20.6.3 is called the Nernst equation, after the German physicist and chemist Walter Nernst (1864–1941), who first derived it. The Nernst equation is arguably the most important relationship in electrochemistry. When a redox reaction is at equilibrium (ΔG = 0), then Equation 20.6.3 reduces to Equation 20.6.4 and 20.6.5 because Q = K, and there is no net transfer of electrons (i.e., Ecell = 0).
since
Substituting the values of the constants into Equation 20.6.3 with T = 298K and converting to base-10 logarithms give the relationship of the actual cell potential (Ecell), the standard cell potential (E°cell), and the reactant and product concentrations at room temperature (contained in Q ):
The Power of the Nernst Equation
The Nernst Equation ( 20.6.3 ) can be used to determine the value of Ecell, and thus the direction of spontaneous reaction, for any redox reaction under any conditions.
Equation 20.6.6 allows us to calculate the potential associated with any electrochemical cell at 298 K for any combination of reactant and product concentrations under any conditions. We can therefore determine the spontaneous direction of any redox reaction under any conditions, as long as we have tabulated values for the relevant standard electrode potentials. Notice in Equation 20.6.6 that the cell potential changes by 0.0591/n V for each 10-fold change in the value of Q because log 10 = 1.
Applying the Nernst equation to a simple electrochemical cell such as the Zn/Cu cell allows us to see how the cell voltage varies as the reaction progresses and the concentrations of the dissolved ions change. Recall that the overall reaction for this cell is as follows: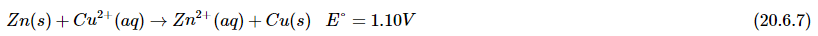
The reaction quotient is therefore Q = [Zn2+]/[Cu2+]. Suppose that the cell initially contains 1.0 M Cu2+ and 1.0 × 10−6 M Zn2+. The initial voltage measured when the cell is connected can then be calculated from Equation 20.6.6: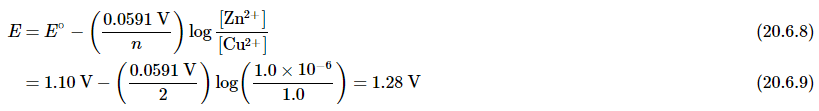
Thus the initial voltage is greater than E° because Q<1 . As the reaction proceeds, [Zn2+] in the anode compartment increases as the zinc electrode dissolves, while [Cu2+] in the cathode compartment decreases as metallic copper is deposited on the electrode. During this process, the ratio Q = [Zn2+]/[Cu2+] steadily increases, and the cell voltage therefore steadily decreases. Eventually, [Zn2+] = [Cu2+], so Q = 1 and Ecell = E°cell. Beyond this point, [Zn2+] will continue to increase in the anode compartment, and [Cu2+] will continue to decrease in the cathode compartment. Thus the value of Q will increase further, leading to a further decrease in Ecell. When the concentrations in the two compartments are the opposite of the initial concentrations (i.e., 1.0 M Zn2+ and 1.0 × 10−6 M Cu2+), Q = 1.0 × 106, and the cell potential will be reduced to 0.92 V.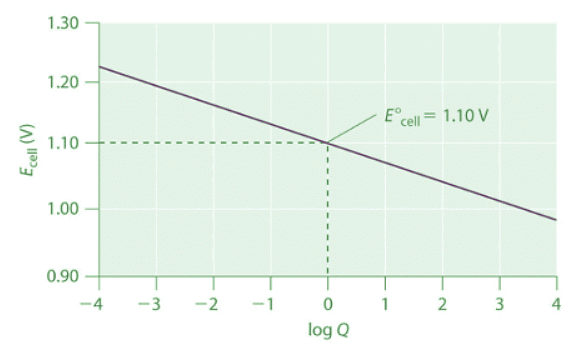 Figure 20.6.1: The Variation of Ecell with Log Q for a Zn/Cu Cell. Initially, log Q < 0, and the voltage of the cell is greater than E°cell. As the reaction progresses, log Q increases, and Ecell decreases. When [Zn2+] = [Cu2+], log Q = 0 and Ecell = E°cell = 1.10 V. As long as the electrical circuit remains intact, the reaction will continue, and log Q will increase until Q = K and the cell voltage reaches zero. At this point, the system will have reached equilibrium.
Figure 20.6.1: The Variation of Ecell with Log Q for a Zn/Cu Cell. Initially, log Q < 0, and the voltage of the cell is greater than E°cell. As the reaction progresses, log Q increases, and Ecell decreases. When [Zn2+] = [Cu2+], log Q = 0 and Ecell = E°cell = 1.10 V. As long as the electrical circuit remains intact, the reaction will continue, and log Q will increase until Q = K and the cell voltage reaches zero. At this point, the system will have reached equilibrium.
The variation of Ecell with log Q over this range is linear with a slope of −0.0591/n, as illustrated in Figure 20.6.1. As the reaction proceeds still further, Q continues to increase, and Ecell continues to decrease. If neither of the electrodes dissolves completely, thereby breaking the electrical circuit, the cell voltage will eventually reach zero. This is the situation that occurs when a battery is “dead.” The value of Q when Ecell = 0 is calculated as follows:
Recall that at equilibrium, Q = K. Thus the equilibrium constant for the reaction of Zn metal with Cu2+ to give Cu metal and Zn2+ is 1.7 × 1037 at 25°C.
Solved Example
Example: The following reaction proceeds spontaneously under standard conditions because E°cell > 0 (which means that ΔG° < 0):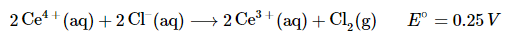
Calculate E for this reaction under the following nonstandard conditions and determine whether it will occur spontaneously: [Ce4+] = 0.013 M, [Ce3+] = 0.60 M, [Cl−] = 0.0030 M, PCl2 = 1.0 atm, and T = 25°C.
Ans: Given: balanced redox reaction, standard cell potential, and nonstandard conditions Asked for: cell potential
Strategy: Determine the number of electrons transferred during the redox process. Then use the Nernst equation to find the cell potential under the nonstandard conditions.
Solution: We can use the information given and the Nernst equation to calculate Ecell. Moreover, because the temperature is 25°C (298 K), we can use Equation 20.6.6 instead of Equation 20.6.3. The overall reaction involves the net transfer of two electrons: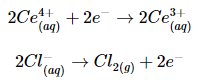
so n = 2. Substituting the concentrations given in the problem, the partial pressure of Cl2, and the value of E°cell into Equation 20.6.6,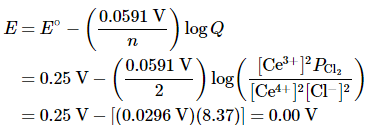
Thus the reaction will not occur spontaneously under these conditions (because E = 0 V and ΔG = 0). The composition specified is that of an equilibrium mixture,
Concentration Cells
A voltage can also be generated by constructing an electrochemical cell in which each compartment contains the same redox active solution but at different concentrations. The voltage is produced as the concentrations equilibrate. Suppose, for example, we have a cell with 0.010 M AgNO3 in one compartment and 1.0 M AgNO3 in the other.
The cell diagram and corresponding half-reactions are as follows:
- cathode:

- anode:

- Overall:

As the reaction progresses, the concentration of Ag+ will increase in the left (oxidation) compartment as the silver electrode dissolves, while the Ag+ concentration in the right (reduction) compartment decreases as the electrode in that compartment gains mass. The total mass of Ag(s) in the cell will remain constant, however. We can calculate the potential of the cell using the Nernst equation, inserting 0 for E°cell because E°cathode = −E°anode: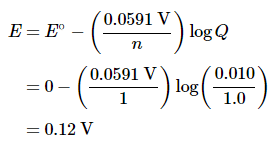
An electrochemical cell of this type, in which the anode and cathode compartments are identical except for the concentration of a reactant, is called a concentration cell. As the reaction proceeds, the difference between the concentrations of Ag+ in the two compartments will decrease, as will Ecell. Finally, when the concentration of Ag+ is the same in both compartments, equilibrium will have been reached, and the measured potential difference between the two compartments will be zero (Ecell = 0).
Solved Example
Example: Calculate the voltage in a galvanic cell that contains a manganese electrode immersed in a 2.0 M solution of MnCl2 as the cathode, and a manganese electrode immersed in a 5.2 × 10−2 M solution of MnSO4 as the anode (T = 25°C).
Ans: Given: galvanic cell, identities of the electrodes, and solution concentrations
Asked for: voltage
Strategy:
A. Write the overall reaction that occurs in the cell.
B. Determine the number of electrons transferred. Substitute this value into the Nernst equation to calculate the voltage.
Solution:
A. This is a concentration cell, in which the electrode compartments contain the same redox active substance but at different concentrations. The anions (Cl− and SO42−) do not participate in the reaction, so their identity is not important. The overall reaction is as follows: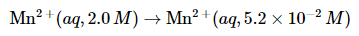
B For the reduction of Mn2+(aq) to Mn(s), n = 2. We substitute this value and the given Mn2+ concentrations into Equation 20.6.6: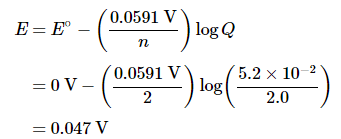
Thus manganese will dissolve from the electrode in the compartment that contains the more dilute solution and will be deposited on the electrode in the compartment that contains the more concentrated solution.
Using Cell Potentials to Measure Solubility Products
Because voltages are relatively easy to measure accurately using a voltmeter, electrochemical methods provide a convenient way to determine the concentrations of very dilute solutions and the solubility products (Ksp) of sparingly soluble substances. As you learned previously, solubility products can be very small, with values of less than or equal to 10−30. Equilibrium constants of this magnitude are virtually impossible to measure accurately by direct methods, so we must use alternative methods that are more sensitive, such as electrochemical methods.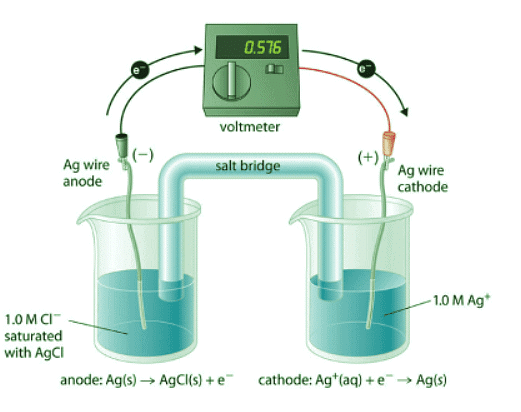
Figure 20.6.1: A Galvanic ("Concentration") Cell for Measuring the Solubility Product of AgCl. One compartment contains a silver wire inserted into a 1.0 M solution of Ag+, and the other compartment contains a silver wire inserted into a 1.0 M Cl− solution saturated with AgCl. The potential due to the difference in [Ag+] between the two cells can be used to determine Ksp.
To understand how an electrochemical cell is used to measure a solubility product, consider the cell shown in Figure 20.6.1, which is designed to measure the solubility product of silver chloride:
In one compartment, the cell contains a silver wire inserted into a 1.0 M solution of Ag+; the other compartment contains a silver wire inserted into a 1.0 M Cl− solution saturated with AgCl. In this system, the Ag+ ion concentration in the first compartment equals Ksp. We can see this by dividing both sides of the equation for Ksp by [Cl−] and substituting: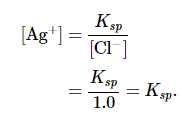
The overall cell reaction is as follows:
Ag+(aq, concentrated) → Ag+(aq, dilute)
Thus the voltage of the concentration cell due to the difference in [Ag+] between the two cells is as follows: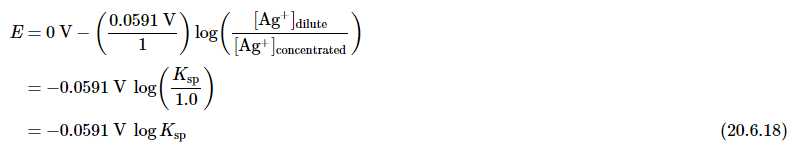
By closing the circuit, we can measure the potential caused by the difference in [Ag+] in the two cells. In this case, the experimentally measured voltage of the concentration cell at 25°C is 0.580 V. Solving Equation 20.6.18 for Ksp,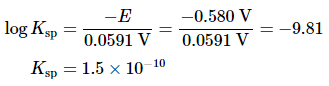
Thus a single potential measurement can provide the information we need to determine the value of the solubility product of a sparingly soluble salt.
Solved Example
Example: Solubility of lead(II) sulfate
To measure the solubility product of lead(II) sulfate (PbSO4) at 25°C, you construct a galvanic cell like the one shown in Figure 20.6.1, which contains a 1.0 M solution of a very soluble Pb2+ salt [lead(II) acetate trihydrate] in one compartment that is connected by a salt bridge to a 1.0 M solution of Na2SO4 saturated with PbSO4 in the other. You then insert a Pb electrode into each compartment and close the circuit. Your voltmeter shows a voltage of 230 mV. What is Ksp for PbSO4? Report your answer to two significant figures.
Ans: Given: galvanic cell, solution concentrations, electrodes, and voltage
Asked for: Ksp
Strategy: A. From the information given, write the equation for Ksp. Express this equation in terms of the concentration of Pb2+.
B. Determine the number of electrons transferred in the electrochemical reaction. Substitute the appropriate values into Equation ??? and solve for Ksp.
Solution: A. You have constructed a concentration cell, with one compartment containing a 1.0 M solution of Pb2+ and the other containing a dilute solution of Pb2+ in 1.0 M Na2SO4. As for any concentration cell, the voltage between the two compartments can be calculated using the Nernst equation. The first step is to relate the concentration of Pb2+ in the dilute solution to Ksp: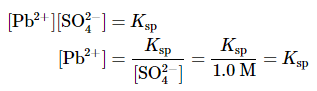
B. The reduction of Pb2+ to Pb is a two-electron process and proceeds according to the following reaction:
Pb2+(aq, concentrated) → Pb2+(aq, dilute)
so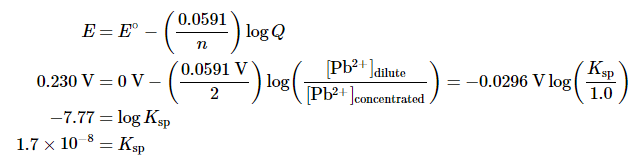
Using Cell Potentials to Measure Concentrations
Another use for the Nernst equation is to calculate the concentration of a species given a measured potential and the concentrations of all the other species. We saw an example of this in Example 20.6.3, in which the experimental conditions were defined in such a way that the concentration of the metal ion was equal to Ksp. Potential measurements can be used to obtain the concentrations of dissolved species under other conditions as well, which explains the widespread use of electrochemical cells in many analytical devices. Perhaps the most common application is in the determination of [H+] using a pH meter, as illustrated below.
Solved Example
Example: Measuring pH
Suppose a galvanic cell is constructed with a standard Zn/Zn2+ couple in one compartment and a modified hydrogen electrode in the second compartment. The pressure of hydrogen gas is 1.0 atm, but [H+] in the second compartment is unknown. The cell diagram is as follows: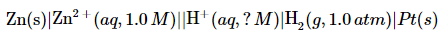
What is the pH of the solution in the second compartment if the measured potential in the cell is 0.26 V at 25°C?
Ans: Given: galvanic cell, cell diagram, and cell potential
Asked for: pH of the solution
Strategy:
A. Write the overall cell reaction.
B. Substitute appropriate values into the Nernst equation and solve for −log[H+] to obtain the pH.
Solution: A. Under standard conditions, the overall reaction that occurs is the reduction of protons by zinc to give H2 (note that Zn lies below H2 in Table P2):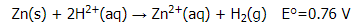
B. By substituting the given values into the simplified Nernst equation (Equation 20.6.6), we can calculate [H+] under nonstandard conditions: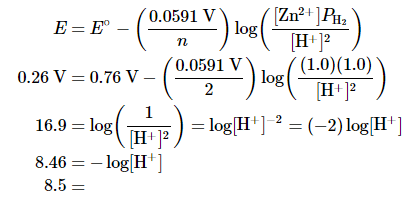
Thus the potential of a galvanic cell can be used to measure the pH of a solution.
Summary
The Nernst equation can be used to determine the direction of spontaneous reaction for any redox reaction in aqueous solution. The Nernst equation allows us to determine the spontaneous direction of any redox reaction under any reaction conditions from values of the relevant standard electrode potentials. Concentration cells consist of anode and cathode compartments that are identical except for the concentrations of the reactant. Because ΔG = 0 at equilibrium, the measured potential of a concentration cell is zero at equilibrium (the concentrations are equal). A galvanic cell can also be used to measure the solubility product of a sparingly soluble substance and calculate the concentration of a species given a measured potential and the concentrations of all the other species.
FAQs on Cell Potential Under Nonstandard Conditions - Chemistry Optional Notes for UPSC
| 1. What is the Nernst equation and how does it relate to the effect of concentration on cell potential? |  |
| 2. How can concentration cells be used to measure solubility products? |  |
| 3. Can cell potentials be used to measure concentrations? |  |
| 4. How does cell potential change under nonstandard conditions? |  |
| 5. What are some practical applications of the Nernst equation and cell potential measurements? |  |















