Circles Chapter Notes | Mathematics Class 10 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Arc and Its Types |

|
| Segment and Relation Between Arcs and Segments |

|
| Cyclic Properties |

|
| Some Important Results |

|
| Solved Examples |

|
Introduction
Imagine a perfectly round wheel rolling smoothly or the orbit of a planet tracing a circular path in the sky—circles are everywhere! In mathematics, a circle is more than just a shape; it’s a fascinating figure defined as a closed curve where every point is equidistant from a fixed point called the center. The constant distance from the center to any point on the circle is the radius, and the boundary is known as the circumference. This chapter dives into the captivating world of circles, exploring their properties, such as chords, arcs, segments, and cyclic quadrilaterals, and uncovering the geometric relationships that make them so special. Let’s embark on this circular journey to understand how these concepts connect and apply in various geometric configurations!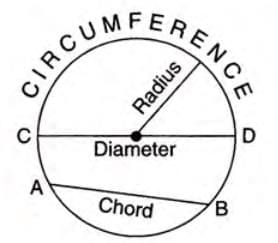
- A circle is a closed curve where all points on the plane are at a constant distance from a fixed point called the center.
- It is the locus of a point moving in a plane such that its distance from the center remains constant.
- The constant distance is called the radius.
- The perimeter of the circle is called the circumference.
Concentric Circles
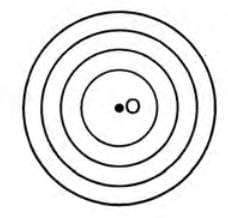
Circles sharing the same center but with different radii are called concentric circles.
Stepwise explanation:
- Identify the common center of the circles.
- Measure the radii of each circle; they must differ for the circles to be concentric.
Equal Circles
Circles are equal or congruent if they have the same radius.
Stepwise explanation:
- Compare the radii of the circles.
- If the radii are equal, the circles are considered equal.
Example: Two circles with radii 4 cm each are equal circles because their radii are identical.
Circumscribed Circle
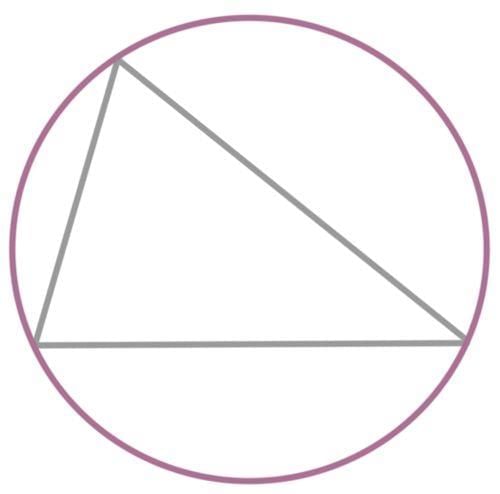
- A circle passing through all vertices of a polygon is called a circumscribed circle.
- The center is called the circumcenter, and the polygon is the inscribed polygon.
- Stepwise explanation:
- Draw a polygon (e.g., a triangle).
- Construct perpendicular bisectors of the sides.
- The intersection point of these bisectors is the circumcenter.
- Draw a circle with the circumcenter as the center, passing through all vertices.
Example: For a triangle ABC, a circle passes through points A, B, and C. The center of this circle is the circumcenter, and the triangle is inscribed in it.
Inscribed Circle
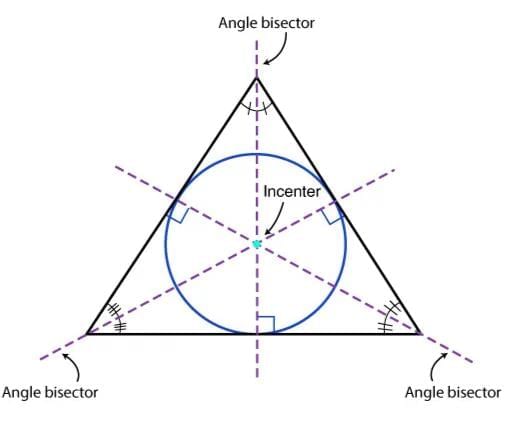
- A circle that touches all sides of a polygon is called an inscribed circle or in-circle.
- The center is called the incenter, and the polygon is the circumscribed polygon.
- Stepwise explanation:
- Draw a polygon (e.g., a triangle).
- Construct angle bisectors from the vertices.
- The intersection point of these bisectors is the incenter.
- Draw a circle with the incenter as the center, touching all sides.
Example: In a triangle ABC, a circle touches sides AB, BC, and CA. Its center is the incenter, and the triangle is the circumscribed polygon.
Chord

- A chord is a line segment joining any two points on the circumference of a circle.
- A chord passing through the center is called a diameter, which is the largest chord.
- Stepwise explanation:
- Identify two points on the circle’s circumference.
- Draw a line segment connecting these points to form a chord.
- If the chord passes through the center, it is a diameter.
Example: In a circle with center O, chord AB joins points A and B on the circumference. If AB passes through O, it is a diameter.
Perpendicular from Center to Chord
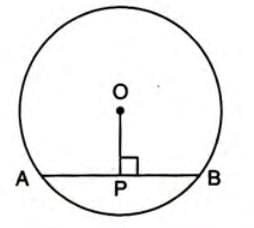
- A line from the center to a chord (not a diameter) that bisects it is perpendicular to the chord.
- Stepwise explanation:
- Draw a circle with center O and a chord AB.
- Draw a line OM from O to the midpoint M of AB.
- OM is perpendicular to AB, and AM = BM.
- AM = BM and ∠OMA = ∠OMB = 90°
Example: In a circle with center O, OM bisects chord AB. Thus, AM = BM, and OM ⊥ AB, so ∠OMA = ∠OMB = 90°.
Perpendicular Bisects Chord
- A perpendicular from the center to a chord bisects the chord.
- Stepwise explanation:
- Draw a circle with center O and a chord AB.
- Draw a line OP perpendicular to AB, intersecting at point P.
- P is the midpoint of AB, so AP = BP.
- AP = BP
Example: In a circle with center O, OP ⊥ AB at point P. Thus, AP = BP, meaning P is the midpoint of chord AB.
Chord Length and Distance from Center
- Larger chords are closer to the center, and smaller chords are farther from the center.
- Stepwise explanation:
- Draw a circle with center O and chords AB and CD, where AB > CD.
- Draw perpendiculars OP to AB and OQ to CD.
- Compare distances: OP < OQ, indicating AB is closer to the center.
Unique Circle Through Three Points
- Exactly one circle passes through three non-collinear points.
- Stepwise explanation:
- Take three points A, B, C not on a straight line.
- Construct perpendicular bisectors of AB and BC.
- Their intersection is the center of the unique circle passing through A, B, C.
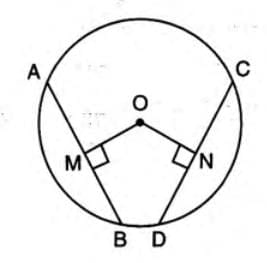
Equal Chords and Distance from Center
- Equal chords are equidistant from the center.
- Stepwise explanation:
- Draw a circle with center O and chords AB = CD.
- Draw perpendiculars OM to AB and ON to CD.
- Measure OM and ON; they are equal, so AB and CD are equidistant.
- If AB = CD, then OM = ON
Equidistant Chords are Equal
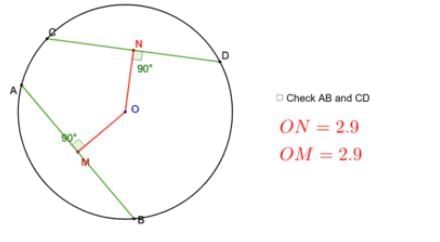
- Chords equidistant from the center are equal in length.
- Stepwise explanation:
- Draw a circle with center O and chords AB and CD, where OM = ON (perpendicular distances).
- Since OM = ON, chords AB and CD have equal lengths.
- If OM = ON, then AB = CD
Example: In a circle with center O, OM = ON for chords AB and CD. Thus, AB = CD.
Arc and Its Types
- An arc is a portion of the circumference of a circle.
- A chord divides the circumference into two arcs.
- Types of arcs:
- Minor arc: Smaller than a semi-circle.
- Major arc: Larger than a semi-circle.
- Stepwise explanation:
- Draw a circle with center O and a chord AB.
- Chord AB splits the circumference into arcs APB (minor) and AQB (major).
Segment and Relation Between Arcs and Segments
- A segment is the region of a circle bounded by an arc and a chord.
- Stepwise explanation:
- Draw a circle with a chord AB.
- The area between chord AB and arc APB is a segment.
Example: In a circle, chord AB and arc APB form a segment, which is the area enclosed between them.
Theorem 5: Angle at Center is Double the Angle at Circumference
- The angle subtended by an arc at the center is twice the angle it subtends at any point on the remaining circumference.
- Stepwise explanation:
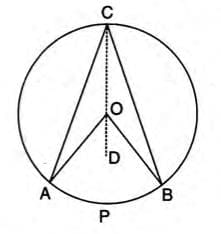
- Draw a circle with center O, arc APB, ∠AOB at the center, and ∠ACB at point C on the circumference.
- Join CO and extend to point D.
- In △AOC, OA = OC (radii), so ∠OAC = ∠OCA.
- Exterior ∠AOD = ∠OAC + ∠OCA = 2∠OCA.
- Similarly, in △BOC, exterior ∠BOD = 2∠OCB.
- Thus, ∠AOB = ∠AOD + ∠BOD = 2(∠OCA + ∠OCB) = 2∠ACB.
- ∠AOB = 2∠ACB
Example: In a circle with center O, arc APB subtends ∠AOB at the center and ∠ACB at point C. If ∠AOB = 110°, then ∠ACB = 110°/2 = 55°.
Theorem 6: Angles in the Same Segment
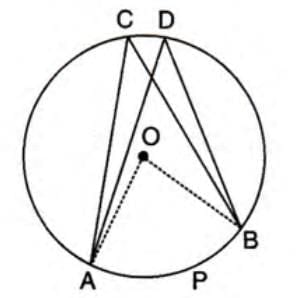
- Angles subtended by the same arc in the same segment are equal.
- Stepwise explanation:
- Draw a circle with center O and arc APB.
- Angles ∠ACB and ∠ADB are subtended by arc APB at points C and D.
- By Theorem 5, ∠AOB = 2∠ACB and ∠AOB = 2∠ADB.
- Thus, ∠ACB = ∠ADB.
- ∠ACB = ∠ADB
Example: In a circle, ∠DAB = ∠DCB because both are subtended by arc DB in the same segment.
Theorem 7: Angle in a Semi-Circle
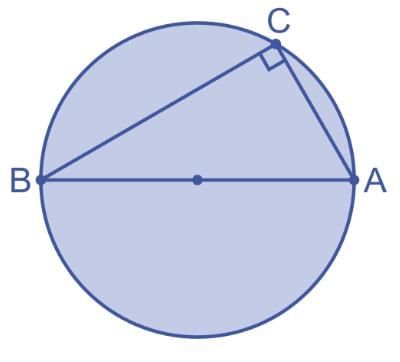
- The angle subtended by a diameter at any point on the circumference is 90°.
- Stepwise explanation:
- Draw a circle with center O and diameter AB.
- Take point C on the circumference, forming ∠ACB.
- Arc APB subtends ∠AOB = 180° (straight line) at the center.
- By Theorem 5, ∠AOB = 2∠ACB, so 180° = 2∠ACB, thus ∠ACB = 90°.
- ∠ACB = 90°
Example: In a circle with center O, AB is a diameter. ∠ACB at point C on the circumference is 90°.
Cyclic Properties
- A quadrilateral with vertices on the circumference of a circle is a cyclic quadrilateral.
- Points lying on the same circle’s circumference are concyclic points.
Example: Quadrilateral ABCD has vertices A, B, C, D on a circle’s circumference, making it a cyclic quadrilateral.
Theorem 8: Opposite Angles of a Cyclic Quadrilateral
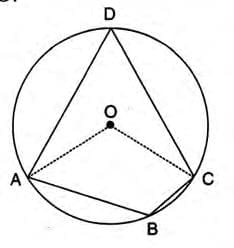
- Opposite angles of a cyclic quadrilateral are supplementary (sum to 180°).
- Stepwise explanation:
- Draw a cyclic quadrilateral ABCD with center O.
- Join OA and OC.
- Arc ABC subtends ∠AOC at the center and ∠ADC at point D.
- By Theorem 5, ∠AOC = 2∠ADC, so ∠ADC = (1/2)∠AOC.
- Similarly, ∠ABC = (1/2) reflex ∠AOC.
- Sum: ∠ABC + ∠ADC = (1/2)(reflex ∠AOC + ∠AOC) = (1/2) × 360° = 180°.
- ∠ABC + ∠ADC = 180°, ∠BAD + ∠BCD = 180°
Theorem 9: Exterior Angle of a Cyclic Quadrilateral
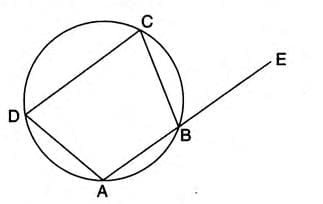
- The exterior angle of a cyclic quadrilateral equals the opposite interior angle.
- Stepwise explanation:
- Draw cyclic quadrilateral ABCD, extend AB to E.
- ∠ABC + ∠CBE = 180° (linear pair).
- ∠ABC + ∠ADC = 180° (opposite angles of cyclic quadrilateral).
- Thus, ∠CBE = ∠ADC.
- ∠CBE = ∠ADC
Example: In cyclic quadrilateral ABCD, side AB is extended to E. If ∠ADC = 80°, then exterior ∠CBE = 80°.
Additional Properties
- If opposite angles of a quadrilateral are supplementary, it is cyclic.
- The angle in a major segment is acute (< 90°).
- The angle in a minor segment is obtuse (> 90°).
Example: In a circle, ∠ABC in the major segment is acute (< 90°), while ∠ADC in the minor segment is obtuse (> 90°).
Some Important Results
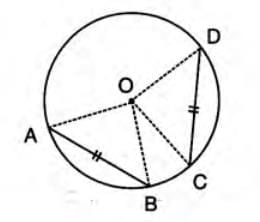
- Equal chords subtend equal angles at the center.
- Stepwise explanation:
- Draw a circle with center O and chords AB = CD.
- Join OA, OB, OC, OD.
- In △AOB and △COD, OA = OC, OB = OD (radii), AB = CD (given).
- By SSS congruence, △AOB ≅ △COD, so ∠AOB = ∠COD.
- If AB = CD, then ∠AOB = ∠COD
- Conversely, if ∠AOB = ∠COD, then chord AB = chord CD.
Example: In a circle with center O, if chord AB = chord CD, then ∠AOB = ∠COD at the center.
Equilateral Triangle in a Circle
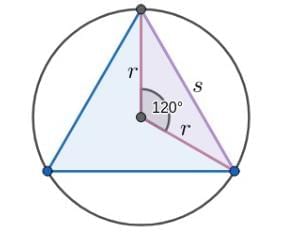
- In an equilateral triangle ABC inscribed in a circle with center O, AB = BC = CA.
- Each angle subtended at the center is 120°.
- Stepwise explanation:
- Draw an equilateral triangle ABC inscribed in a circle with center O.
- Since AB = BC = CA = s, chords are equal.
- Thus, ∠AOB = ∠BOC = ∠AOC = 360°/3 = 120°.
- ∠AOB = ∠BOC = ∠AOC = 120°
Regular Polygons in a Circle
- For a regular polygon inscribed in a circle, the central angle for each side is 360°/n, where n is the number of sides.
- Stepwise explanation:
- Draw a regular polygon (e.g., square, pentagon) inscribed in a circle with center O.
- Divide 360° by the number of sides to find the central angle.
- Central angle = 360°/n
Chord Ratios and Angles
- If chords AB and CD have lengths in ratio m:n, the angles they subtend at the center are also in ratio m:n.
- Stepwise explanation:
- Draw chords AB and CD with AB:CD = m:n.
- The central angles ∠AOB and ∠COD are proportional to the chord lengths.
- If AB:CD = m:n, then ∠AOB:∠COD = m:n
Example: If chord AB:chord CD = 7:5, then ∠AOB:∠COD = 7:5.
Solved Examples
Example 1: In a circle with center O, ∠AOC = 110°.
Calculate (i) ∠ADC, (ii) ∠ABC, (iii) ∠OAC.
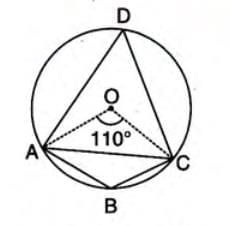 (i) ∠ADC = (1/2)∠AOC = (1/2) × 110° = 55° (Angle at center is twice the angle at circumference).
(i) ∠ADC = (1/2)∠AOC = (1/2) × 110° = 55° (Angle at center is twice the angle at circumference).
(ii) ∠ABC + ∠ADC = 180° (opposite angles of cyclic quadrilateral). So, ∠ABC + 55° = 180°, thus ∠ABC = 125°.
(iii) In △AOC, OA = OC (radii), so ∠OAC = ∠OCA. Sum of angles: ∠OAC + ∠OCA + ∠AOC = 180°. Thus, 2∠OAC + 110° = 180°, so ∠OAC = 35°.
Example 2: In a circle with center O, AC is a diameter, AB = BC, and ∠AED = 118°.
Calculate (i) ∠DEC, (ii) ∠DAB.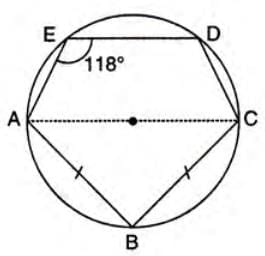 (i) Join EC. ∠AEC = 90° (angle in semi-circle). ∠DEC = ∠AED - ∠AEC = 118° - 90° = 28°.
(i) Join EC. ∠AEC = 90° (angle in semi-circle). ∠DEC = ∠AED - ∠AEC = 118° - 90° = 28°.
(ii) Join AD. ∠DAC = ∠DEC = 28° (angles in same segment). In △ABC, AB = BC, so ∠BAC = ∠BCA = 45° (angles opposite equal sides). ∠ABC = 90° (angle in semi-circle). Thus, ∠DAB = ∠DAC + ∠BAC = 28° + 45° = 73°.
Example 3: In a circle with center O, chords AC and BD are perpendicular, ∠OAB = a, ∠DBC = b. Show that a = b.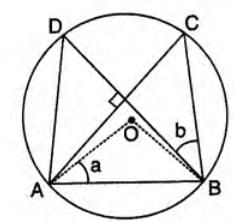
- In △AOB, OA = OB (radii), so ∠OBA = ∠OAB = a. Thus, ∠AOB = 180° - 2a.
- ∠ACB = (1/2)∠AOB = (1/2)(180° - 2a) = 90° - a (angle at center is twice angle at circumference).
- Since AC ⊥ BD, ∠ACB + ∠DBC = 90°. Thus, 90° - a + b = 90°, so a = b.
|
74 videos|213 docs|30 tests
|
FAQs on Circles Chapter Notes - Mathematics Class 10 ICSE
| 1. What are the different types of arcs in a circle? |  |
| 2. How do segments relate to arcs in a circle? |  |
| 3. What are cyclic properties in relation to circles? |  |
| 4. Can you explain some important results related to circles? |  |
| 5. What are some common examples of problems involving arcs and segments in circles? |  |














