Cylinder, Cone and Sphere Chapter Notes | Mathematics Class 10 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Cylinder |

|
| Hollow Cylinder |

|
| Cone |

|
| Sphere |

|
| Spherical Shell |

|
| Hemisphere |

|
| Conversion of Solids |

|
| Combination of Solids |

|
| Miscellaneous Problems |

|
Introduction
Imagine shaping clay into a tall water tank, a pointy ice-cream cone, or a perfectly round football. These shapes—cylinders, cones, and spheres—are not just fascinating to look at but are also all around us in everyday life. From water pipes to party hats, understanding their surface areas and volumes helps us solve real-world problems, like calculating how much paint is needed for a cylindrical drum or how much ice cream fits in a conical cup. This chapter takes you on an exciting journey through these 3D shapes, unraveling their properties with simple formulas and practical examples. Let’s dive into the world of mensuration and explore how to measure these solids!
Cylinder
- A cylinder is a solid with a uniform circular cross-section, like a can or a pipe.
- It has two parallel circular bases connected by a curved surface.
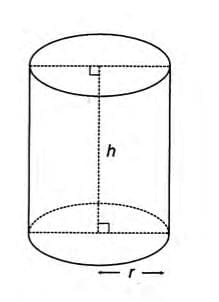
Formulas:
- Area of cross-section = πr2
- Circumference of cross-section = 2πr
- Curved surface area = 2πrh
- Total surface area = 2πrh + 2πr2 = 2πr(h + r)
- Volume = πr2h
Example: The area of the curved surface of a cylinder is 4,400 cm2 and the circumference of its base is 110 cm. Find the height and volume.
- Step 1: Curved surface area = 2πrh = 4,400 cm2, and circumference = 2πr = 110 cm.
- Step 2: Divide the curved surface area by circumference: h = 4,400 ÷ 110 = 40 cm.
- Step 3: Find radius: 2πr = 110, so r = 110 ÷ (2 × 22/7) = 35/2 cm.
- Step 4: Volume = πr2h = (22/7) × (35/2)2 × 40 = 38,500 cm3.
Answer: Height = 40 cm, Volume = 38,500 cm3.
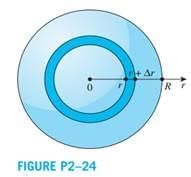
Hollow Cylinder
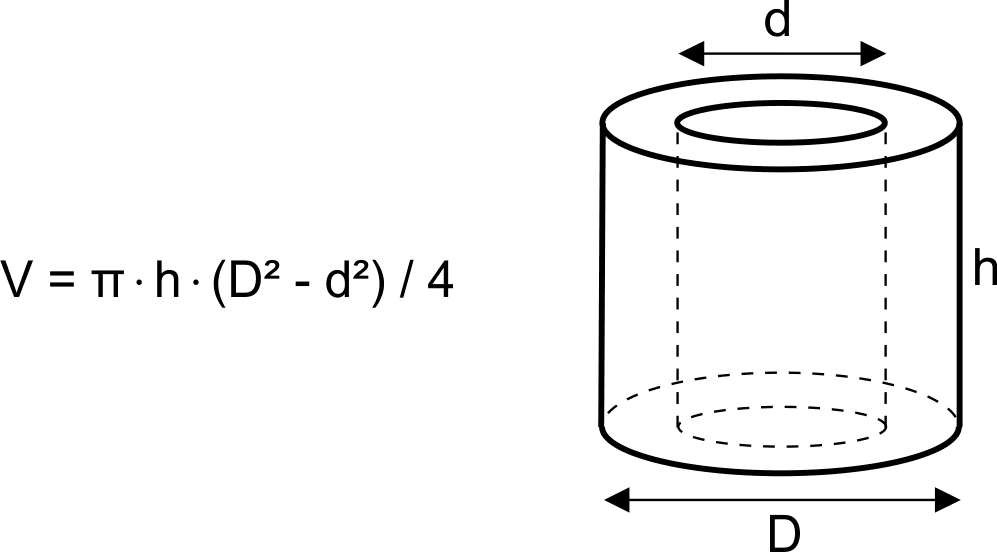 Hollow Cylinder Volume
Hollow Cylinder Volume- A hollow cylinder has an inner and outer circular surface, like a pipe or a straw.
- It has an external radius (R), internal radius (r), and height (h).
- Thickness of wall = R - r
- Area of cross-section = π(R2 - r2)
- External curved surface area = 2πRh
- Internal curved surface area = 2πrh
- Total surface area = 2πRh + 2πrh + 2π(R2 - r2)
- Volume of material = π(R2 - r2)h
- Determine the external radius (R), internal radius (r), and height (h).
- Calculate the thickness by subtracting r from R.
- Find the cross-sectional area by subtracting the inner circle area from the outer.
- Compute external and internal curved surfaces using their respective radii.
- For total surface area, sum both curved surfaces and the area of the annular bases.
- For volume, multiply the cross-sectional area by the height.
Example:. Cylindrical tube, open at both ends, has an internal diameter of 11.2 cm, length 21 cm, and metal thickness of 0.4 cm. Calculate the volume of the metal.
- Step 1: Internal radius (r) = 11.2 ÷ 2 = 5.6 cm.
- Step 2: External radius (R) = 5.6 + 0.4 = 6.0 cm.
- Step 3: Volume of metal = π(R2 - r2)h = (22/7) × (62 - 5.62) × 21.
- Step 4: Calculate: (62 - 5.62) = 36 - 31.36 = 4.64, so volume = (22/7) × 4.64 × 21 = 306.24 cm3 ≈ 306.2 cm3.
Answer: Volume = 306.2 cm3.
Cone
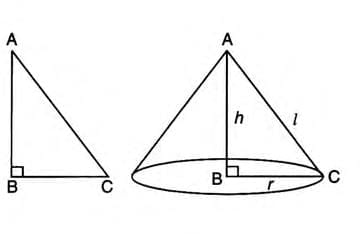
- A cone is formed by revolving a right-angled triangle around one of its sides (not the hypotenuse), like a party hat.
- It has a circular base (radius r), height (h), and slant height (l).
- Slant height: l2 = h2 + r2
- Volume = (1/3)πr2h
- Curved surface area = πrl
- Total surface area = πrl + πr2 = πr(l + r)
- Identify the radius (r), height (h), and find slant height (l) using the Pythagorean theorem.
- Calculate volume by multiplying the base area by height and dividing by 3.
- Find curved surface area by multiplying π, radius, and slant height.
- Add the base area to the curved surface area for total surface area.
Example:A cone has a base radius of 7 cm and height of 24 cm. Find its volume and total surface area.
- Step 1: Slant height: l = √(242 + 72) = √(576 + 49) = 25 cm.
- Step 2: Volume = (1/3) × (22/7) × 72 × 24 = 1,232 cm3.
- Step 3: Total surface area = πr(l + r) = (22/7) × 7 × (25 + 7) = 704 cm2.
Answer: Volume = 1,232 cm3, Total surface area = 704 cm2.
Sphere
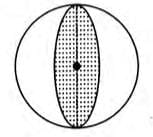
- A sphere is formed by revolving a circle around its diameter, like a ball.
- It has a radius (r).
- Volume = (4/3)πr3
- Surface area = 4πr2
- Identify the radius (r).
- For volume, multiply (4/3) by π and r3.
- For surface area, multiply 4 by π and r2.
Example:. sphere’s surface area is 616 cm2. Find its volume.
- Step 1: Surface area = 4πr2 = 616, so r2 = 616 × 7 ÷ (4 × 22) = 49, r = 7 cm.
- Step 2: Volume = (4/3) × (22/7) × 73 = 1,437 (1/3) cm3.
Answer: Volume = 1,437 (1/3) cm3.
Spherical Shell
 Spherical Shell Volume
Spherical Shell Volume- A spherical shell is the solid between two concentric spheres, like a hollow ball.
- It has an external radius (R) and internal radius (r).
Formula:
- Volume = (4/3)π(R3 - r3)
- Identify the external (R) and internal (r) radii.
- Calculate the volume by subtracting the inner sphere’s volume from the outer sphere’s volume.
Example: A hollow sphere with internal and external diameters 4 cm and 8 cm is melted into a cone with base diameter 8 cm. Find the cone’s height.
- Step 1: Internal radius (r) = 2 cm, external radius (R) = 4 cm.
- Step 2: Volume of spherical shell = (4/3)π(43 - 23) = (4/3)π × 56.
- Step 3: Cone’s radius = 4 cm, volume = (1/3)π × 42 × h.
- Step 4: Equate volumes: (1/3)π × 16h = (4/3)π × 56, so h = 14 cm.
Answer: Height = 14 cm.
Hemisphere
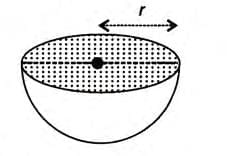
- A hemisphere is half a sphere, formed by cutting a sphere through its center.
- Volume = (2/3)πr3
- Total surface area = 3πr2
- For volume, use half the sphere’s volume formula.
- For total surface area, add the curved surface (2πr2) and the base area (πr2).
Example:A hollow hemispherical vessel has internal and external diameters of 42 cm and 45.5 cm. Find its capacity and outer curved surface area.
- Step 1: Internal radius (r) = 21 cm, external radius (R) = 22.75 cm.
- Step 2: Capacity = (2/3)πr3 = (2/3) × (22/7) × 213 = 19,404 cm3.
- Step 3: Outer curved surface area = 2πR2 = 2 × (22/7) × 22.752 = 3,253.25 cm2.
Answer: Capacity = 19,404 cm3, Outer curved surface area = 3,253.25 cm2.
Conversion of Solids
 Sphere Conversion
Sphere ConversionConversion involves melting one solid and recasting it into another, keeping the volume constant.
- Calculate the volume of the original solid.
- Equate it to the volume of the new solid to find unknown dimensions.
- Solve for the required dimension or number of new solids formed.
Example:. sphere of radius 10.5 cm is melted and recast into small cones of radius 3.5 cm and height 3 cm. Find the number of cones.
- Step 1: Volume of sphere = (4/3)π × 10.53.
- Step 2: Volume of one cone = (1/3)π × 3.52 × 3.
- Step 3: Number of cones = [(4/3)π × 10.53] ÷ [(1/3)π × 3.52 × 3] = 126.
Answer: Number of cones = 126.
Combination of Solids
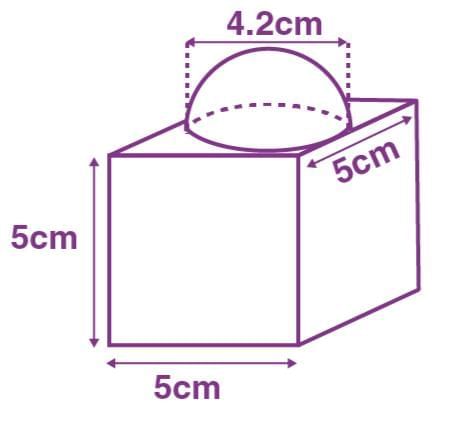 Combination Solids
Combination SolidsCombination solids are made by joining two or more solids, like a cone on a hemisphere.
- Calculate the volume or surface area of each solid separately.
- For volume, add the volumes of all solids.
- For surface area, add the exposed surfaces, subtracting any overlapping areas.
Example:. toy is a cone mounted on a hemisphere, both with a radius of 6 cm. The cone’s height is 8 cm. Find the surface area and volume (π = 3.14).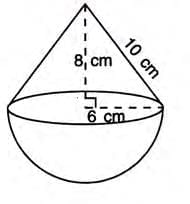
- Step 1: Slant height of cone: l = √(82 + 62) = 10 cm.
- Step 2: Surface area = πrl + 2πr2 = 3.14 × (6 × 10 + 2 × 62) = 414.48 cm2.
- Step 3: Volume = (1/3)πr2h + (2/3)πr3 = 3.14 × [(1/3) × 62 × 8 + (2/3) × 63] = 753.6 cm3.
Answer: Surface area = 414.48 cm2, Volume = 753.6 cm3.
Miscellaneous Problems
 Cylindrical Solid
Cylindrical SolidThese involve complex solids with cavities or combinations of shapes.
- Identify the solids and their dimensions.
- Calculate the volume or surface area of the main solid.
- Subtract the volume or adjust the surface area for any cavities or added parts.
Example: A cylinder (height 36 cm, radius 14 cm) has a conical cavity (radius 7 cm, height 24 cm) drilled out. Find the volume and total surface area of the remaining solid.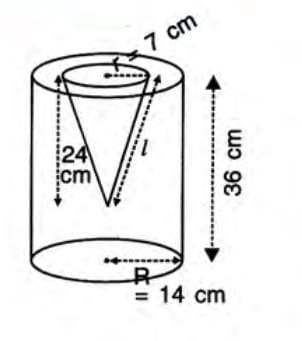
- Step 1: Cylinder volume = π × 142 × 36 = (22/7) × 196 × 36 = 22,176 cm3.
- Step 2: Cone volume = (1/3)π × 72 × 24 = (1/3) × (22/7) × 49 × 24 = 1,232 cm3.
- Step 3: Remaining volume = 22,176 - 1,232 = 20,944 cm3.
- Step 4: Cone’s slant height: l = √(242 + 72) = 25 cm.
- Step 5: Surface area = πR2 + 2πRH + π(R2 - r2) + πrl = (22/7) × [142 + 2 × 14 × 36 + (142 - 72) + 7 × 25] = 4,796 cm2.
Answer: Volume = 20,944 cm3, Total surface area = 4,796 cm2.
|
74 videos|213 docs|30 tests
|
FAQs on Cylinder, Cone and Sphere Chapter Notes - Mathematics Class 10 ICSE
| 1. What is the formula for the volume of a cylinder, and how is it derived? |  |
| 2. How do you find the surface area of a hollow cylinder? |  |
| 3. What is the relationship between the volume of a cone and its height? |  |
| 4. How do you calculate the volume of a sphere? |  |
| 5. What is the difference between a solid sphere and a spherical shell in terms of volume? |  |



















