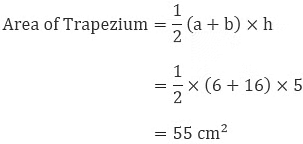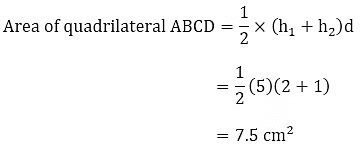Mensuration Chapter Notes | Mathematics (Maths) Class 8 PDF Download
| Table of contents |

|
| Introduction |

|
| Area of a Polygon |

|
| Solid Shapes |

|
| Surface Area Of Cube, Cuboid and Cylinder |

|
| Volume of Cube, Cuboid, and Cylinder |

|
Introduction
In this chapter, we'll be calculating the area of complex shapes like Polygons (quadrilaterals), and dive into finding the surface area and volume of 3D solids such as cubes, cuboids, and cylinders. Get ready to explore advanced geometry concepts!
Area of a Polygon
To find the area of a quadrilateral, we can split it into triangles and calculate the area of each one. This approach also works for more complex shapes like polygons. Let’s take a look at the Pentagon:
By drawing one diagonal, AD, and dropping perpendiculars BF and CG from points B and C, the pentagon ABCDE is divided into four parts. The total area of the pentagon is the sum of the areas of right-angled triangles AFB and CGD, the trapezium BFGC, and the triangle AED.
(Can you spot the parallel sides in trapezium BFGC?)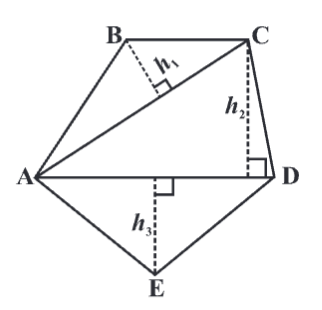
Alternatively, by drawing two diagonals, AC and AD, the pentagon can be split into three triangles. In this case, the total area of the pentagon is the sum of the areas of triangles ABC, ACD, and AED.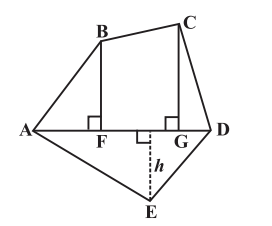
This method of breaking down complex shapes into simpler parts makes calculating the area much easier!
There is no particular formula for the area of the polygon so we need to divide it into a possible number of figures like a triangle, rectangle, trapezium and so on. By adding the area of all the split figures we will get the area of the required polygon.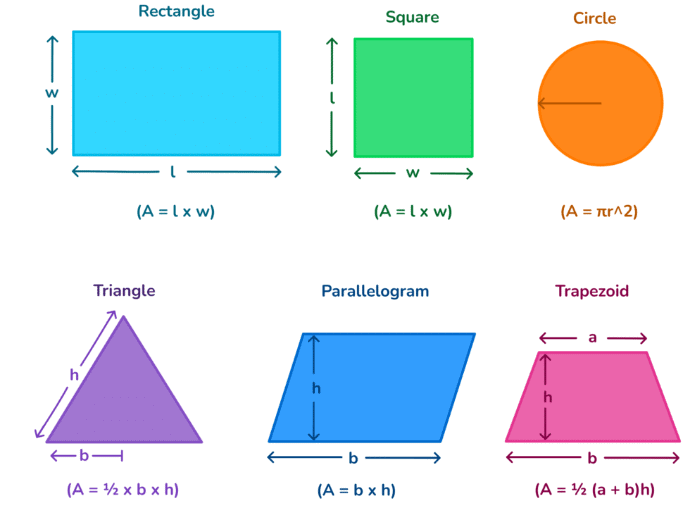
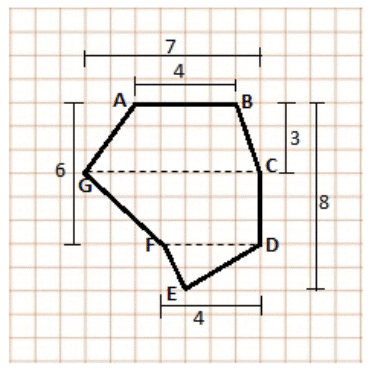
Example 1: Find the area of polygon ABCDEFG. The measurements (in cm) are shown in the figure.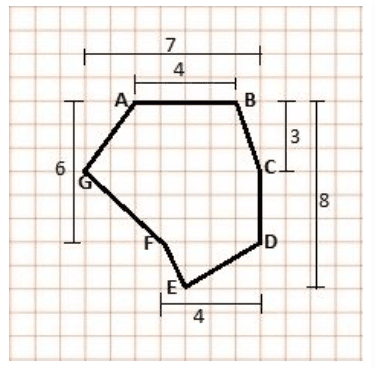
Solution: The polygon can be split into two trapeziums and a triangle.
So, the area of polygon ABCDEFG is given by the sum of the area of trapezium ABCG and CDFG and the area of triangle DEF.
Height of trapezium ABCG = 3 cm
Height of trapezium CDFG = (6 – 3) = 3 cm
Height of triangle DEF = (8 – 6) = 2 cm
Area of trapezium ABCG = (sum of parallel sides) × height/2 = (4 + 7)×3/2 = 33/2 = 16.5 cm2
Area of trapezium CDFG = (7 + 4) ×3/2 = 33/2 = 16.5 cm2
Area of triangle DEF = (base ×height)/2 = (4 × 2)/2 = 8/2 = 4 cm2
So, area of polygon ABCDEFG = area of ABCG + area of CDFG + area of DEF
= 16.5 + 16.5 + 4 = 37 cm2
Let's study in deep Trapezium, Rhombus and General Quadrilateral.
(i) Area of Trapezium
A trapezium is a quadrilateral whose two sides are parallel. And if its non-parallel sides are equal then it is said to be an isosceles trapezium.
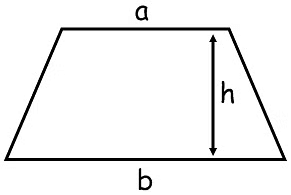
We can find the Area of Trapezium by following these steps:
1. By Splitting the figure
One way to find the Area of trapezium is to divide it into two or three plane figures and then find the area.
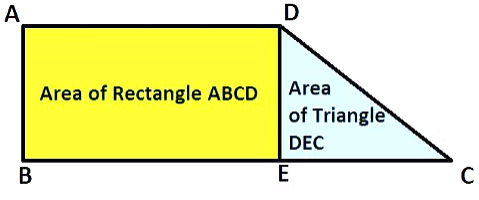
In the trapezium ABCD,
It can be divided into two parts i.e. a rectangle and a triangle.
Area of ABCD = Area of ABED + Area of DEC
2. By using the formula
Another way is to calculate the area by using a formula. Area of trapezium ishalfof the product of the summation of the parallel sides and the perpendicular distance between them.
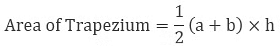
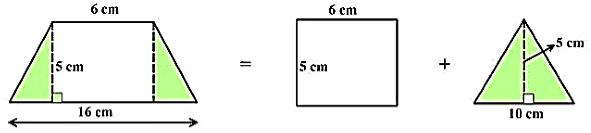
Example 2: Find the area of the trapezium whose parallel sides are 6 cm and 16 cm, with a height of 5 cm. Calculate the area using both methods.
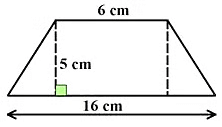
Solution:
Splitting the trapezium we get –
Area of the trapezium = Area of rectangle + Area of triangle
= (6 x 5) + (1/2) x 5 x 10
= 30 + 25
= 55 cm2
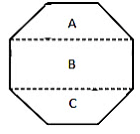
Example: Find the area of the given octagon.
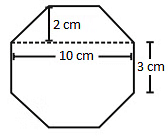
Solution:We can divide the given octagon into three parts.
Two trapezium A and B and one rectangle shown by part B.
Two trapezium A and B and one rectangle shown by part B.
Area of A = Area of B = (1/2) × (a + b) × h= (1/2) x (10 + 3) × 2
= 13 cm2.
Remark: We should use the formula most of the time if possible as it is the quick and easy method.
(ii) Area of a Rhombus
The area of a rhombus can be calculated using its base and height with the help of the formula,
Area of rhombus = base × height.
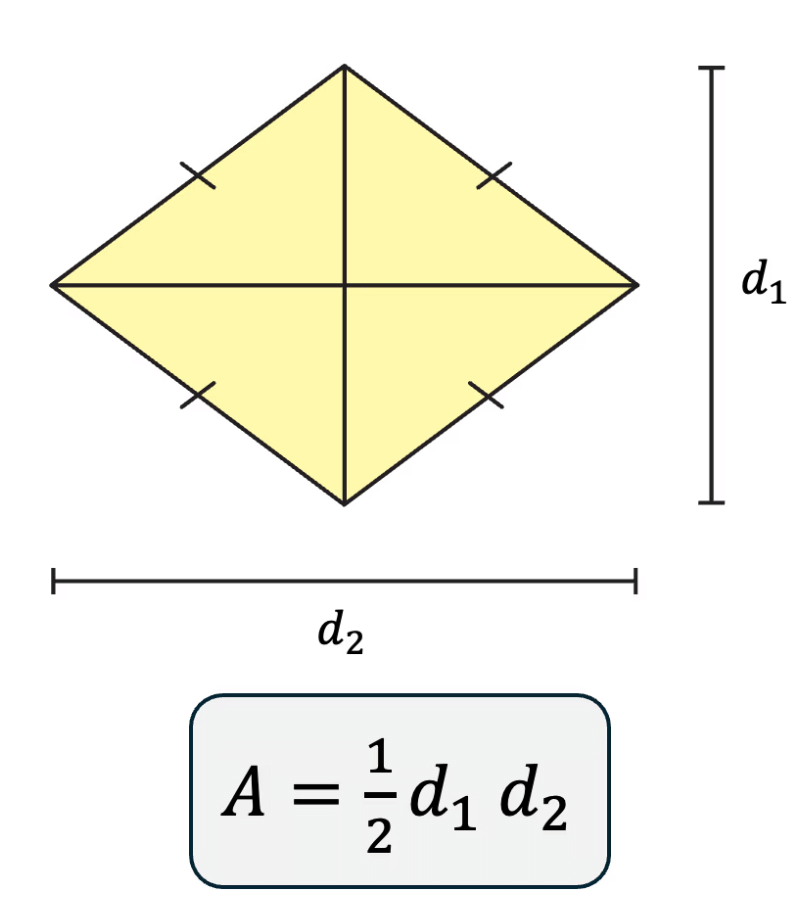
Another way to find the area of a rhombus is by using its diagonals. So, this formula is expressed as:
Area of rhombus = ½ × d1 × d2
where d1 and d2 are the lengths of the diagonals.
Example 3: Find the area of a rhombus having base of 12 m and height is 16 m.
Solution:
Base, b = 12 mHeight, h = 16 m
Area (A) = b × h
A = (12 × 16) m2
A = 192 m2
Thus, the area of the rhombus is 192 m2
(iii) General Quadrilateral
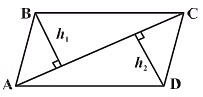
To find the area of any quadrilateral:
We can divide it into two triangles and then the area can be easily calculated by calculating the area of both the triangles separately.
Area of ABCD = Area of ∆ABC + Area of ∆ACD
= (1/2) × AC × h1 + (1/2) × AC× h2
The formula for the Area of a General Quadrilateral

Where h1 and h2 are the height of both the triangles and d is the length of the common diagonali.e. AC.
Example 4: Find the area of quadrilateral ABCD.

Solution:In the quadrilateral ABCD,
BD is the common diagonal so d = 5 cm.
Height of the two triangles are h1 = 2 cm and h2 = 1 cm.
Solid Shapes
The 3-dimensional shapes which occupy some space are called solid shapes.
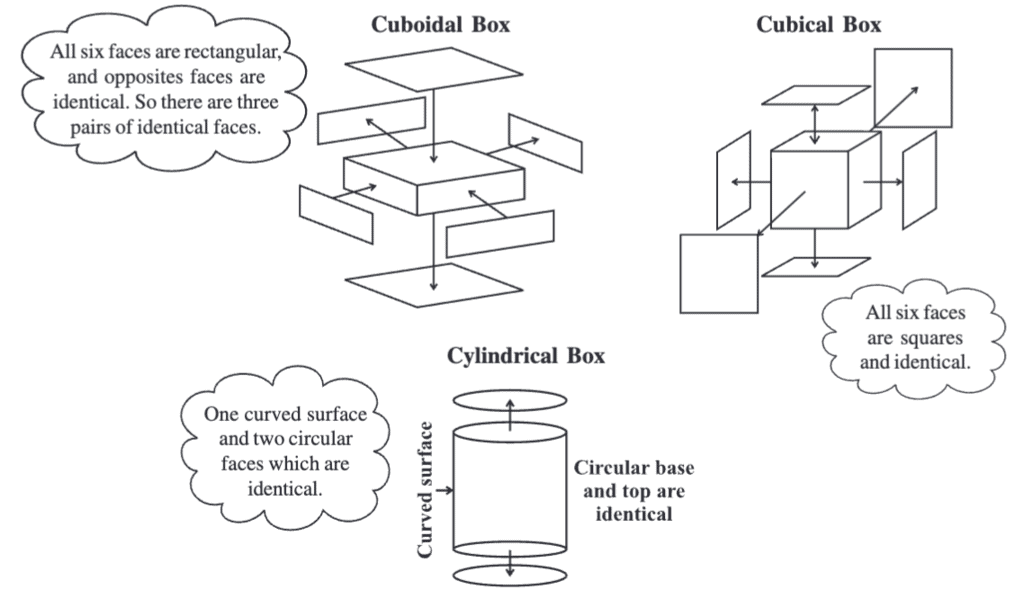
Surface Area Of Cube, Cuboid and Cylinder
If we draw the net of the solid shape then we can see it’s all the faces clearly and if we add the areas of all the faces then we get the total surface area of that solid shape. The unit of surface area is a square unit.
Total Surface Area
The total surface area of an object is the total area covered by the outer surfaces of that object. It is essentially the sum of the areas of all the flat surfaces, also known as faces. For example, in a cuboid, the surface area is calculated by adding up the areas of all six rectangular faces.
Lateral or Curved Surface Area
If we leave the top and bottom faces of the solid shape then the area of the rest of the figure is the lateral surface of the shape. The unit of lateral surface area is a square unit.
1. Surface Area of Cuboid
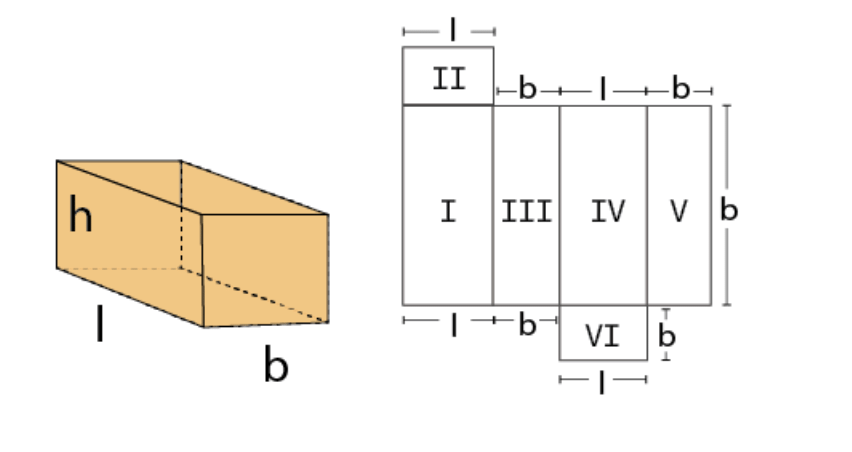
- Total Surface area of cuboid =2 (lb + bh + lh)
- Lateral Surface area of cuboid =2h (l + b)
- Where l is the length, b is the breadth and h is the height.
Example 5: The internal measures of a farmer's grain storage room are 10 m × 7 m × 5 m. Find the total cost of painting all four walls of the room if the cost of painting is ₹6 per m². What will be the cost if the ceiling of the room is also painted?
Solution:Let the length of the room = l=10m
Width of the room = b=7m
Height of the room = h=5mArea of the four walls of the room
Area of four walls = Perimeter of the base × Height of the room = 2(l + b) = 2(10 + 7)
Area of four walls = 34 × 5 = 170 m2
Cost of painting four walls
Cost of painting per m2 = ₹6
Total cost of painting four walls = 170 × 6 = ₹1020
Area of the ceiling
Area of ceiling = l × b = 10 × 7 = 70m2
Cost of painting the ceiling
Cost of painting the ceiling = 70 × 6 = ₹420
Final Total Cost:
Total cost of painting the room (walls + ceiling) = ₹1020 + ₹420 = ₹1440
So, the total cost of painting the room, including the ceiling is ₹1440.
2. Surface Area of Cube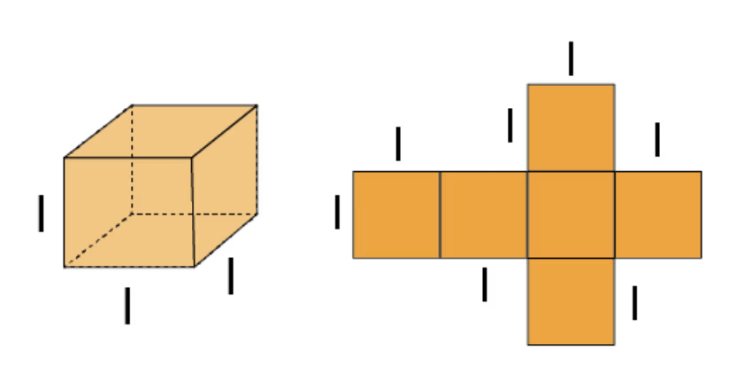
- Total Surface area of a cube =6l2
- Lateral Surface area of a cube =4l2
- Where l is the length of each side of the cube.
Example 6: A carpenter is polishing a wooden box in the shape of a cube, with each side measuring 6 m. The cost of polishing is ₹4 per m². Find the total cost of polishing the entire surface area of the cube.
Solution:Let the side length of the cube = a = 6m
Total surface area of the cube
Surface area of a cube = 6 × side2
= 6 × (6)2
= 6 × 36
= 216 m2Cost of polishing per m²
Cost per m2 = ₹4
Total cost of polishing the cube
Total cost = 216 × 4 = ₹864
So, the total cost of polishing the cube is ₹864.
3. Surface Area of Cylinder
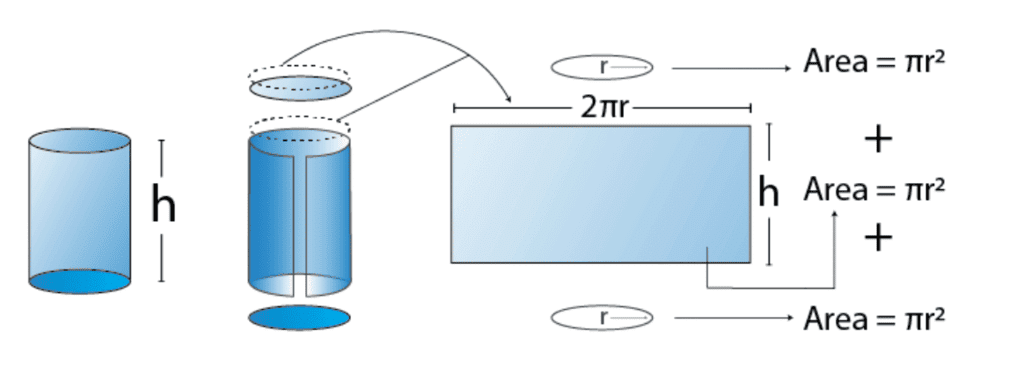
- Curved surface area of cylinder (C.S.A) = 2πrh
- Total Surface area of cylinder(T.S.A) = 2πr(r+h)
- Where, r is the radius of the cylinder and h is the height of the cylinder.
Example 7: A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label.
Solution:-
a) 12 m²
b) 66 m²
c) 94 m²
d) 72 m²
Volume
Volume is the space occupied by any solid figure i.e. the amount of capacity to carry something is the volume of that solid shape. The unit of volume is a cubic unit.
For example, the volume of a room is greater than the volume of an almirah inside it, and the volume of a pencil box is greater than the pen and eraser inside it.
Measurement of Volume: Volume is measured in cubic units (e.g., cubic cm /cm3, cubic m/ m3 ).
Cubic Units:
Formulas are used to calculate the volume of different shapes like cuboids, cubes, and cylinders. These will be addressed individually for better understanding.
Volume of Cube, Cuboid, and Cylinder
(i) Volume of Cuboid
Consider a cuboid having Length, Width, and Height to be l, w, and h respectively. Then,
The Volume of a cuboid is given by the product of its dimensions.
Volume = l × w × h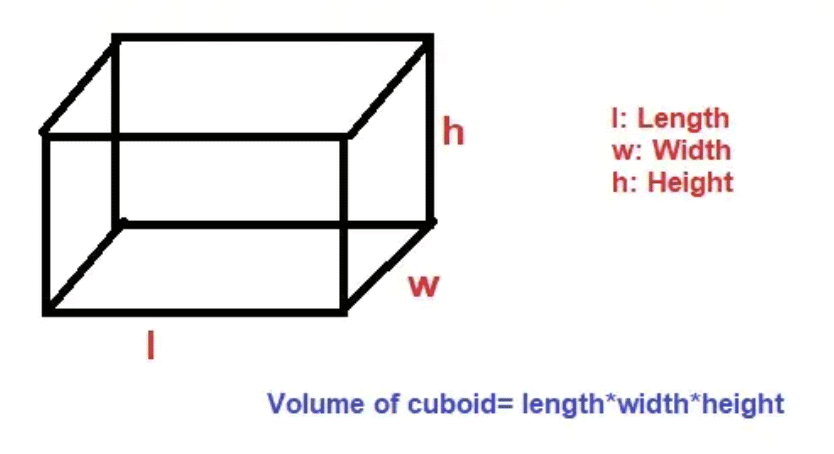
Example 8: Find the volume of a cuboid whose length = 5 cm, width = 2 cm and height = 3 cm.
Solution: Given: length = 5 cm, width = 2 cm and height = 3 cmBy the formula, we know;
Volume of cuboid = length x width x height
= 5 cm x 2 cm x 3 cm
= 30 cu.cm.
(ii) Volume of the Cube
A Cuboid having all the dimensions to be of equal length is known to be a cube. Consider the dimension of a cube to be “a” then the volume of a cube is given as:
Volume of a cube = a × a × a= a3

Example 9: Calculate the amount of air that can be accumulated in a cube of side 3 m.
Solution: Amount of air that can be accumulated in a cube = capacity of the cube = volume of cubeVolume of cube = a3 = 3 × 3 × 3 = 27 m3
Thus, the amount of air accumulated in a cube of 3 m side = 27 m3
(iii) Volume of a Cylinder
A cylinder can be seen as a set of circular disks that are stacked on one another. In order to calculate the space occupied by a cylinder, we calculate the space occupied by each disk and then add them up. Thus, the volume of the cylinder can be given by the product of the area of base and height. There are many other properties of Cylinder.
Consider a cylinder having a base radius of ‘r’ and height to be ‘h,’ thus the volume of a cylinder is given by:
Volume of a cylinder = (area of base) × h = πr2 h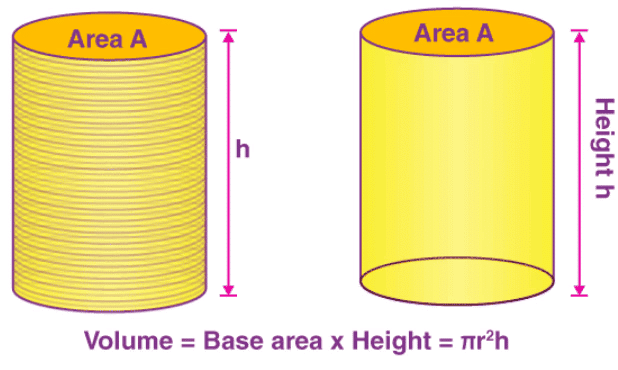
Example 10: Calculate the radius of the base of a cylindrical container of volume 220 m3. The height of the cylindrical container is 70 m. (Take pi = 22/7)
Solution:
Volume of a cylinder = (area of base) × height of a cylinderArea of base = (Volume of cylinder)/ (height of cylinder) = 220/70 m2
22/7 r2 = 220/70
r2 = 1
r = 1
Volume and Capacity
- Volume and capacity are one and the same thing.
- Volume is the amount of space occupied by a shape.
- Capacity is the quantity that a container can hold.
- Capacity can be measured in the form of litres.
We can see the relation between litre and cm3 as,
1 L = 1000 mL
1 mL = 1 cm3,
1 L = 1000 cm3.
Thus, 1 m3 = 1000000 cm3 = 1000 L.
Example 10: A cuboidal block of silver is 9 cm long, 4 cm broad and 3.5 cm in height. From it, beads of volume 1.5 cm3 each are to be made. Find the number of beads that can be made from the block.
Solution:Given details are,
Length of a cuboidal block of silver = 9cm
Breadth = 4cm
Height = 3.5cm
Volume of a cuboid = l × b × h
= 9 × 4 × 3.5 = 126cm3
So, Number of beads of volume 1.5cm3 that can be made from the block =
Volume of silver block/volume of one bead
= 126cm3/1.5cm3
= 84 beads
Example 11: A village, having a population of 4000, required 150 litres water per head per day. It has a tank which is 20 m long, 15 m broad and 6 m high. For how many days will the water of this tank last?
Solution:Given details are,
Population of village = 4000
Dimensions of water tank = 20m × 15m × 6m
Water required per head per day = 150 litres
Total requirement of water per day = 150 × 4000 = 600000 litres
Volume of water tank = l × b × h
= 20 × 15 × 6
= 1800m3
= 1800000 litres
We know that,
Number of days water last in the tank = volume of tank / total requirement
= 1800000/600000
= 3 days
∴ Water in the tank last for 3 days.
|
81 videos|423 docs|31 tests
|
FAQs on Mensuration Chapter Notes - Mathematics (Maths) Class 8
| 1. What is the formula to calculate the area of a polygon? |  |
| 2. How do you find the surface area of a cube? |  |
| 3. What is the difference between the surface area and volume of a cylinder? |  |
| 4. How can the volume of a cuboid be calculated? |  |
| 5. What are solid shapes and how do they differ from 2D shapes? |  |