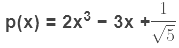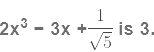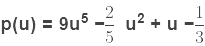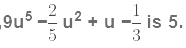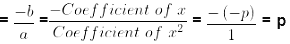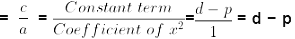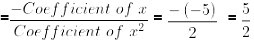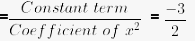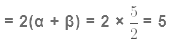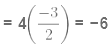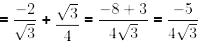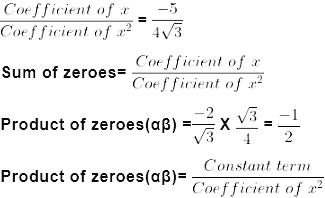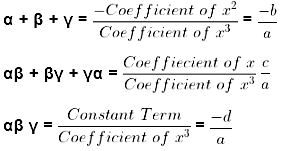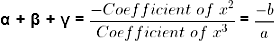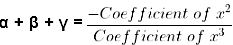Polynomials Class 10 Notes Maths Chapter 2

Algebraic Expressions

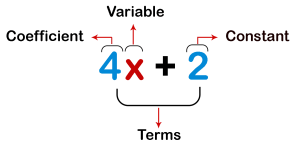
An algebraic expression is a combination of numbers, letters (representing variables), and symbols used for mathematical operations.

Algebraic Expressions

Polynomial

An expression using mathematical operations such as addition, subtraction, multiplication, and division can include fractional exponents.

On the other hand, a polynomial is a mathematical expression consisting of variables and coefficients where the exponent of each variable is a non-negative integer.

Degree of a Polynomial

For a polynomial in one variable – the highest exponent on the variable in a polynomial is the degree of the polynomial.

Degree of a Polynomial

Types of Polynomials 

a) Monomial – A polynomial with just one term. Example: 2x, 6x², 9xy

b) Binomial – A polynomial with two unlike terms. Example: 4x²+x, 5x+4

c) Trinomial – A polynomial with three unlike terms. Example: x²+3x+4

Example 1: Write the degree of the following Polynomials.

i) 
Sol: As the highest power of x in p(x) is 3. The degree of polynomial,
ii) 
Sol: As the highest power of u in p(u) is 5. The degree of the polynomial,

Example 2: Identify the type of the Polynomials given below (on the basis of degree)

i) 2y + 6
Sol: Here, the highest power of y in the given polynomial is 1, so it is a Linear Polynomial
ii) √2 + y²  + y
Sol: Here, the highest power of y in the given polynomial is 2, so it is a Quadratic Polynomial.
iii) y³ + 4y² + 2y + 1
Sol: Here, the highest power of y in the given polynomial is 3, so it is a Cubic Polynomial.

Zeroes of a Polynomial

If p(x) is a polynomial in x and k is any real number, then the value obtained by replacing x by k in p(x), is called the value of p(x) at x = k, and is denoted by p(k).

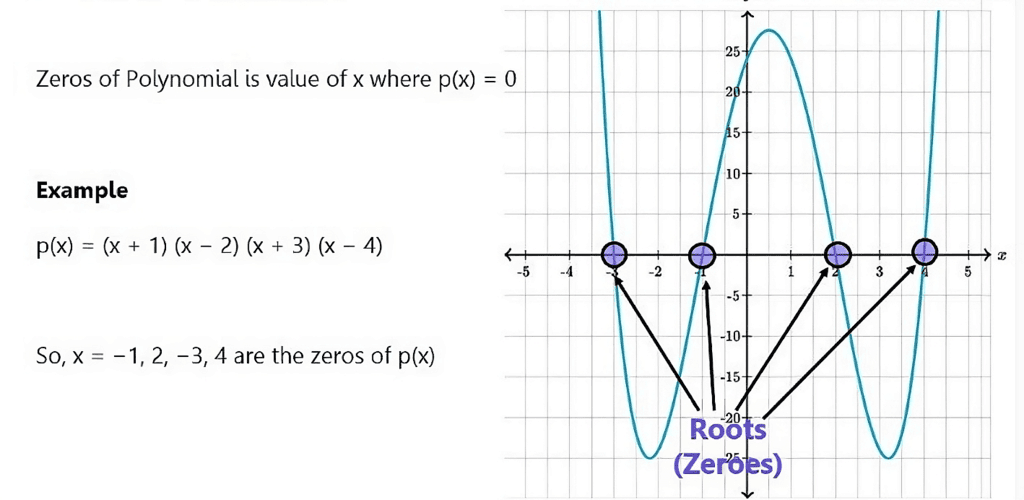Zeroes of a Polynomial

Let us consider the polynomial p(x) = 2x³ − 3x² + 1
If we put x = 2 in the polynomial, that is, we replace x by 2 in the given polynomial, we get,
p(2) = 2(2)³ − 3(2)² + 1 = 16 − 12 + 1 = 5
Therefore, the value of the polynomial p(x) at x = 2 is 5, that is, p(2) = 5
Similarly, we can find the value of p(x) at x = 0,
p(0) = 2(0)³ − 3(0)² + 1 = 0 − 0 + 1 = 1
The value of p(x) at x = 0 is 1, that is, p(0) = 1
Now consider another case where we find the value of p(x) at x = 1
p(1) = 2(1)³ − 3(1)² + 1 = 2 − 3 + 1 = 3 − 3 = 0
Here, we see that the value of the polynomial p(x) is 0 at x = 1
As p(1) = 0, 1 is called a zero of the polynomial
p(x) = 2x³ − 3x² + 1
A real number k is said to be a zero of the polynomial p(x) if p(k) = 0.
Now consider a linear polynomial,p(x) = 2x + 1,
If k is a zero of p(x), then p(k) = 0
2k + 1 = 0
2k = −1
k = -1/2
If k is a zero of a polynomial, p(x) = ax + b, then,
p(k) = ak + b = 0
k = -b/a
Therefore, the zero of the polynomial, ax + b = -b/a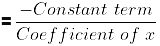

Example 3: If 3 is a zero of polynomial,p(x) = 2x² + 3x − 9a, then find the value of a.

Sol:

If 3 is a zero of the polynomial, p(x) = 2x² + 3x − 9a then p(3) = 0
Now, p(x) = 2x² + 3x − 9a
p(3) = 2(3)² + 3(3) − 9a
Now we will equate p(3) to 0.
2(3)² + 3(3) − 9a = 0
18 + 9 − 9a = 0
27 − 9a = 0
27 = 9a
a = 3
∴ The value of a = 3.

Example 4: For what value of k, -2 is a zero of the polynomial 3x² + 4x + 2k.

Sol:

If -2 is a zero of the polynomial, p(x) = 3x² + 4x + 2k then p(−2) = 0
Now, p(x) = 3x² + 4x + 2k
As -2 is a zero of p(x), we will replace x by -2 in the given polynomial and equate it to 0.
p(−2) = 3(−2)² + 4(−2) + 2k = 0
12 − 8 + 2k = 0
2k = −4
k = −2

Example 5: If 1 and 2 are zeroes of a polynomial p(x) = 2x² − kx + 2m, then find the value of k and m.

Sol:

Here, 1 and 2 are zeroes of the polynomial,
p(x) = 2x² − kx + 2m
So, p(1) = 2(1)² − k(1) + 2m = 0
2 − k + 2m = 0
k = 2m + 2 →(i)
Now p(2) = 2(2²)− k(2) + 2m = 0
8 − 2k + 2m = 0
Putting the value of k in the above equation, we get
 8 − 2(2m + 2) + 2m = 0
8 − 4m − 4 + 2m = 0
4 − 2m = 0
2m = 4
m = 2
We will now find the value of k by putting m = 2 in equation (i)
k = 2(2) + 2
k = 4
∴ k = 4 and m = 2

Geometrical Meaning of Zeroes of Polynomial

We know that a real number k is a zero of the polynomial p(x) if p(k) = 0.
A linear polynomial is of the form ax + b where a ≠ 0.
We will first study the graph of a linear polynomial, y = x + 3
If we put x = 2 in the above equation, we get
y = 2 + 3 = 5
Similarly, we can find more values of y by putting different values of x.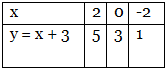

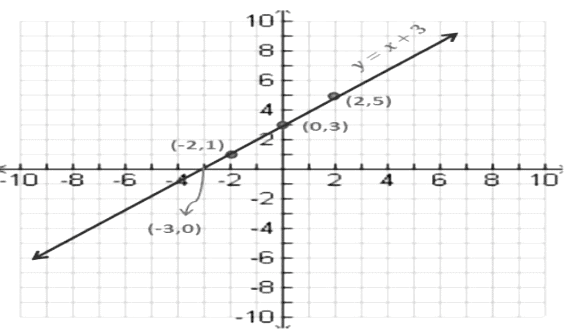Here, we can see that the graph of a linear polynomial is a straight line.
The graph of y = x + 3 intersects the x − axis at x = −3
Thus, −3 is the zero of the linear polynomial, y = x + 3.
Therefore, the zero of the polynomial, x + 3 is the x −coordinate of the point where the graph of y = x + 3 intersects the x-axis.

• For a linear polynomial ax + b, where a ≠ 0, the graph of y = ax + b is a straight line that intersects the x-axis at exactly one point, that is, (-b/a, 0)
• Therefore, the linear polynomial ax + b has exactly one zero, namely the x −coordinate of the point where the graph of y = ax + b intersects the x-axis.

Next, we will study the geometrical meaning of a zero of a quadratic polynomial.
Consider a quadratic polynomial, x² − 4
First, we will find some values of y = x² − 4 corresponding to some values of x.
If we plot these points on a graph, this is how the graph will look like.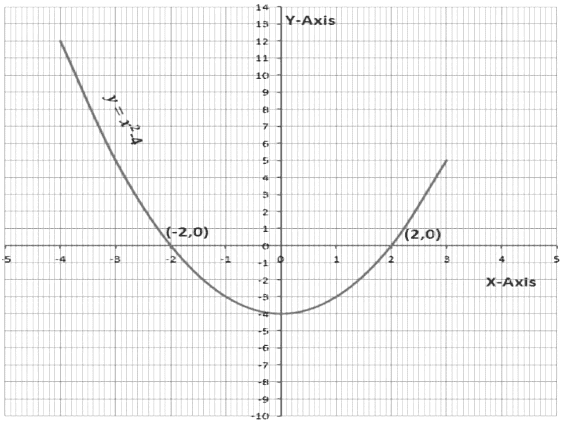

For that matter, any quadratic polynomial y = ax² + bx + c, where a ≠ 0 the graph will have either one of the two shapes depending on the value of a
i) If a > 0, then the shape is open upwards.
ii) If a < 0, then the shape is open downwards
These curves are called parabolas.
If we see the graph, then -2 and 2 are the points on the x- axis where the graph of y = x² − 4 intersects the x-axis.
Therefore -2 and 2 are the zeroes of the polynomial x² − 4.
The zeroes of a quadratic polynomial ax² + bx + c, a ≠ 0 are the x − coordinates of the point, where the parabola representing y = ax² + bx + c intersects the x − axis.
According to the shape of the graph of y = ax² + bx + c, the following cases may arise.

Case 1: 
In this case, the graph intersects the x-axis at two distinct points A and A′, then the x- coordinates of A and A′are the two zeroes of the quadratic polynomial ax² + bx + c.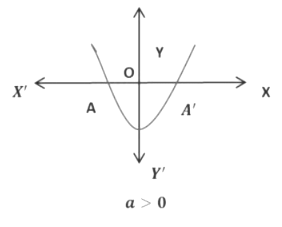

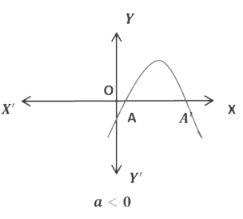
Case 2:
In this case, the graph cuts the x − axis at exactly one point. Therefore, the two points A and A′of Case 1 coincide here to become one point A.

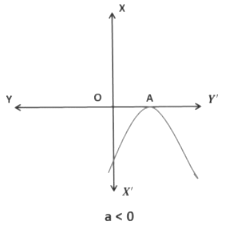Here, the x- coordinate of A is the only zero for the quadratic polynomial, ax² + bx + c.

Case 3:
In the third case, the graph is either completely above x-axis or completely below x-axis. Therefore, the graph does not intersect the x-axis at any point. Thus, the quadratic polynomial has no zero.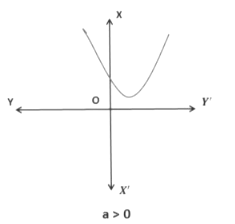

So, after studying all the cases we can see that a quadratic polynomial can have,

• Two distinct zeroes ( shown in case 1)
• Two equal zeroes or one zero ( shown in case 2)
• No zero (shown in case 3)

Therefore, geometrically we can see that a quadratic polynomial can have either two distinct zeroes or two equal zeroes that are one zero or no zero. Thus a quadratic polynomial of degree 2 has at most 2 zeroes.
Now we will study the geometrical meaning of the zeroes of a cubic polynomial. Consider a cubic polynomial x³ − 4x. First, we will find some values of y corresponding to a few values of x.
If we plot these points on the graph, the graph will look like this,

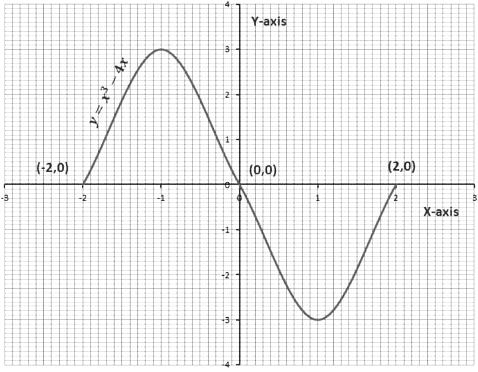If we observe the graph, we see that -2, 0 and 2 are the x-coordinate of the points where the graph of y = x³ − 4x intersect the x-axis. Thus -2, 0 and 2 are the zeroes of the cubic polynomial, y = x³ − 4x.
We will draw the graphs of a few more cubic polynomials.
Let us first consider the cubic polynomial, y = x³. We will find a few values of x and y.
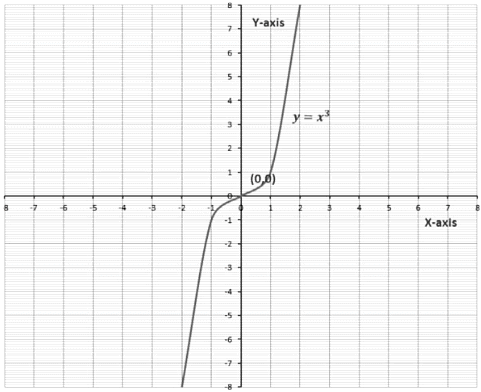If we observe the graph we see that 0 is the only zero of the cubic polynomial, y = x³ as its graph intersects the x-axis at the origin only.
Now consider one more cubic polynomial, y = x³ − x. We will again find a few values of x and y.

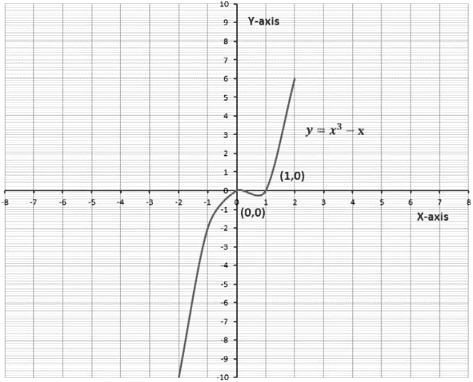Now, we can see in the graph that 0 and 1 are the two zeroes of the cubic polynomial, y = x³ − x as its graph is intersecting the x-axis at (0, 0) and (1, 0).
Therefore, any cubic polynomial can have at most 3 zeroes.

Example 6: The graph of y = p(x) is given, for some polynomials p(x). Find the number of zeroes of p(x) in each case.

Sol:

(a)
This is a graph of a quadratic polynomial. As the graph of y = p(x) does not intersect the x – axis at any point. Thus, it has no zero.
(b)
This is again a graph of a quadratic polynomial. Here, the graph of y = p(x) intersects the x- axis at two points. Hence the number of zeroes is 2.
(c)

This is a graph of a linear polynomial. The number of zeroes is 1. As the graph of y = p(x) is intersecting the x-axis at one point only.
(d)
The given graph is of a cubic polynomial. Here the polynomial y = p(x) is intersecting the x – axis at 3 points. Therefore, the number of zeroes is 3.

Example 7: Which of the following is not the graph of a cubic polynomial?

Sol:
Option d) is not the graph of a cubic polynomial. It is a graph of a quadratic polynomial, as the graph is in the shape of a parabola which is opening downwards.

Relationship between Zeroes and Coefficients of a Polynomial

We know that a quadratic polynomial is of the form ax² + bx + c. A quadratic polynomial can have at the most two zeroes.

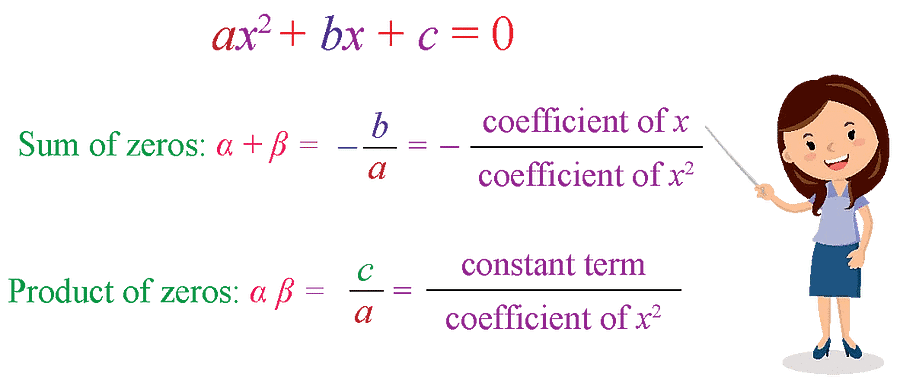Sum and Product of ZeroesIn general, if α and β are the zeroes of the quadratic polynomial p(x) = ax² + bx + c, a ≠ 0, then x − α and x − β are the actors of the p(x). Therefore,
ax² + bx + c = k (x - a) (x - β)
= k(x² - xβ - ax + aβ)
= [x² - (β + a)x + aβ)
= kx² - k (β + a)x + kaβ
Now, comparing the coefficients of x², x and constant terms on both sides, we get
a = k, b = -k(β + a), c = kaβ
(a + β) = -b/k
Now k = a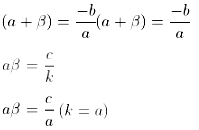

Sum of zeroes(α + β)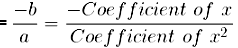

Product of zeroes(αβ)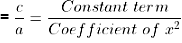

Example 8: If one zero of 2x² − 3x + k is reciprocal to the other, then find the value of k.

Sol:

Let one zero be α, then the other zero will be  1/a
We know that, Product of zeroes(αβ) = c/a = Constant term / Coefficient of x²  

 = c/a = k/2
 K= 2

Example 9: If α and β are zeroes of the polynomial x² − p(x + 1) + d such that (α + 1)(β + 1) = 0, then find the value of d.

Sol:

The given polynomial is x² − p(x + 1) + d
x² − px − p + d
Comparing the above equation with ax² + bx + c, we get
a = 1, b = −p, c = −p + d
α and β are the zeroes of the polynomial x² − px − p + d
Sum of zeroes(α + β)
Product of zeroes(αβ)
(α + 1)(β + 1) = 0 (given)
αβ + α + β + 1 = 0
Putting (α + β) = p and (αβ) = d − p in the above equation we get,
d − p + p + 1 = 0
d + 1 = 0
d = −1

Example 10: Form a quadratic polynomial, whose one zero is 7 and the product of zeroes is -56.

Sol:

Let the zeroes be α and β.
It is given that the value of one zero is 7, then let us assume that α = 7
Product of zeroes = αβ = 7β
Now, 7β = −56
β = −8
∴ α = 7 and β = −8
(α + β) = 7 − 8 = −1
(αβ) = 7 × (−8) = −56
We know that a quadratic polynomial is 

x² −(sum of zeroes)x + product of zeroes
x² − (α + β)x + (αβ)
Putting (α + β) = −1 and (αβ) = −56
x² + x − 56

Example 11: If the zeroes of the polynomial x² + px + q are double in value of the zeroes of 2x² − 5x − 3, then find the value of p and q.

Sol:

Let α and β be the zeroes of 2x² − 5x − 3.
Sum of zeroes(α + β) =−ba
Product of zeroes(αβ) = c/a =
As the zeroes of x² + px + q are double in value. Therefore, 2α and 2β are the zeroes of x² + px + q
Sum of zeroes(2α + 2β) = 2(α + β)
Product of zeroes(2α × 2β) = 4αβ
We know that a quadratic polynomial is x² −(sum of zeroes)x + product of zeroes
∴ x² − (2α + 2β)x + (2α × 2β)
x² − 5x − 6
Comparing the above equation with x² + px + q, we get
p = −5, q = −6

Example 12: Find the zeroes of the quadratic polynomial, 4√3x² + 5x − 2√3 and verify the relationship between the zeroes and the coefficients.

Sol:

Letp(x) = 4√3x² + 5x − 2√3
By splitting the middle term we get,
p(x) = 4√3x² + 5x − 2√3
p(x) = 4√3x² + (8 − 3)x − 2√3
p(x) = 4√3x² + 8x − 3x − 2√3
p(x) = 4x(√3x + 2) − √3(√3x + 2)
p(x) = (√3x + 2)(4x − √3)
The value of 4√3x² + 5x − 2√3 is zero, when x =-2/√3 and x = √3/4
Therefore, the zeroes of 4√3x² + 5x − 2√3 are x = -2/√3 and x = √3/4
Sum of zeroes(α + β)

Let α, β, γ be the zeroes of a cubic polynomial
ax³ + bx² + cx + d

x³ −(sum of zeroes)x² + (sum of the product of zeroes taking two at a time)x – product of zeroes
x³ +( α + β + γ)x² + (αβ + βγ + γα)x – αβ γ

Example 13: If two zeroes of the polynomial f(x) = x³ − 4x² − 3x + 12 are √3 and −√3, then find its third zero.

Sol:

Let α and β be the two roots of the polynomial,
x³ − 4x² − 3x + 12
Then α = √3 and β = - √3,

√3 - √3 + y = -(4)/1 = 4
γ = 4
Therefore the third zero is 4.

Example 14: If zeroes of the polynomial f(x) = x³ − 3x² + x + 1 are a − b, a and a + b, then find a and b.

Sol:

Now, a − b, a, and a + b are zeroes of the cubic polynomial
Let α = a − b, β = a and γ = a + b
We know that,

a − b + a + a + b = -(3)/1 = 3
3a = 3 , a = 1 

(a − b)a(a + b) = -(1)/1 = 1
a(a² − b²) = −1
Putting a = 1 in the above equation
1(1 − b²) = −1
(1 − b²) = −1
b² = 2
b = ±√2

Division algorithm of Polynomials (Deleted from NCERT)

If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find the polynomial q(x) and r(x) such that,
p(x) = g(x) × q(x) + r(x)
where(x) = 0 or degree of r(x)
This result is known as the Division Algorithm for polynomials.
p(x) → Dividend
g(x) → Divisor
q(x) → Quotient
r(x) → Remainder
Thus , Dividend = Divisor × Quotient + Remainder
First, we will study the method of dividing one polynomial by another with the help of an example.
Divide x³ − 6x² + 11x − 6 by x + 2
i) Firstly, arrange the terms of the dividend and the divisor in descending order of the degrees (also known as writing the polynomial in standard form). In this case, the dividend and divisor are in the standard form.
ii) To obtain the first term of the quotient, we will divide the highest degree term of the dividend,x3 by the highest degree term of the divisor, x. We get the first term of the quotient, x and carry out the division process. What remains is −8x² + 11x.
iii) To obtain the second term of the quotient divide the highest degree term of the new dividend (−8x²) by the highest degree term of the divisor, x. We get −8x and what remains is 27x − 6. As the degree of 27x − 6 is equal to the degree of the divisor, (x + 2) We will continue the division process.
iv) The new dividend, 27x − 6 is now divided by (x + 2), the third term of the quotient will be 27 and the remainder is -60. As the degree of reminder is less than the divisor, we stop our division process.
Dividend p(x) = x³ − 6x² + 11x − 6
Divisor g(x) = x + 2
Quotient q(x) = x² − 8x + 27
Remainder r(x) = 60
p(x) = g(x) × q(x) + r(x)

Example 15: On dividing x³ − 3x² + 5x − 3 by a polynomial g(x), the quotient and remainder will be x² + x − 3 and 8 respectively.

Sol:

Find g(x).
Let Dividend p(x) = x³ − 3x² + 5x − 3
Quotient q(x) = x − 3
Remainder r(x) = 7x − 9
We have to g(x).
By using division Algorithm, we have
p(x) = g(x) × q(x) + r(x)
Putting the values of p(x), q(x) and g(x) we get,
x³ − 3x² + 5x − 3 = g(x) × x − 3 + 7x − 9
x³ − 3x² + 5x − 3 − 7x + 9 = g(x) × x − 3
x³ − 3x² + 5x − 7x − 3 + 9 = g(x) × x − 3
x³ − 3x² − 2x + 6 = g(x) × x² + x − 3

On dividing x³ − 3x² + 5x − 3 by x − 3 we get,
Quotient q(x) = x² − 2

Example 15: If a polynomial, x⁴ + x³ + 8x² + px + q, is exactly divisible by x² + 1, then find the value of p and q.

Sol:

Here, p(x) = x⁴ + x³ + 8x² + px + q
g(x) = x² + 1
On dividing p(x) by g(x) we get,
As x⁴ + x³ + 8x² + px + q is exactly divisible by x² + 1, the remainder should be equal to zero.
(p − 1)x + q − 7 = 0
(p − 1)x + q − 7 = 0x + 0
Comparing the coefficient of x and constant term, we get
(p − 1) = 0
p = 1
q − 7 = 0
q = 7
∴ p = 1 and q = 7