Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Chapter Notes: Quadratic Equations
Quadratic Equations Chapter Notes | Mathematics Class 10 ICSE PDF Download
| Table of contents |
|
| Introduction |
|
| To Examine the Nature of the Roots |
|
| Solving Quadratic Equations by Factorisation |
|
| Solving Quadratic Equations Using the Formula |
|
| Equations Reducible to Quadratic Equations |
|
Introduction
Dive into the fascinating world of quadratic equations, where numbers and variables dance together to form equations with a touch of elegance! In this chapter, you'll explore equations where the highest power of the variable is two. From understanding their standard form to solving them with various methods, quadratic equations are like puzzles waiting to be solved. Get ready to master the art of finding solutions and discovering the nature of roots!
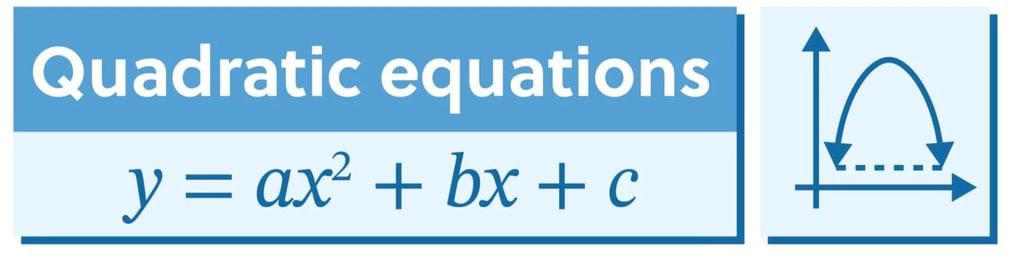
- A quadratic equation is an equation with one variable where the highest power is two.
- It is written in the form ax2 + bx + c = 0, where a, b, and c are real numbers, and a ≠ 0.
- Every quadratic equation has two solutions, known as roots.
- The expression b2 - 4ac is called the discriminant, denoted by D.
- Discriminant formula: D = b2 - 4ac.
- An adfected quadratic equation has a square term and a linear term, e.g., 4x2 + 5x = 0.
- A pure quadratic equation has only the square term, e.g., x2 = 4.
Example: 3x2 + 4x + 7 = 0 is a quadratic equation because the highest power of x is 2.
To Examine the Nature of the Roots
- The nature of roots (real, imaginary, equal, or unequal) depends on the discriminant D = b2 - 4ac.
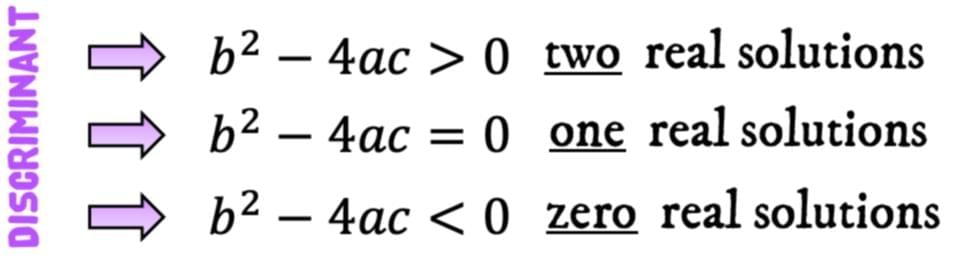
- Every rational and irrational number is a real number.
- The square root of a negative number is imaginary, e.g., √(-4) is imaginary.
Example 1: For 5x2 - 6x + 7 = 0,
a = 5, b = -6, c = 7.
Discriminant D = (-6)2 - 4 × 5 × 7 = 36 - 140 = -104.
Since D < 0, the roots are imaginary.
Example 2: Find the value of m if the roots of (4 + m)x2 + (m + 1)x + 1 = 0 are equal.
- Identify a = 4 + m, b = m + 1, c = 1.
- For equal roots, D = 0, so b2 - 4ac = 0.
- Calculate: (m + 1)2 - 4(4 + m) × 1 = 0.
- Expand: m2 + 2m + 1 - 16 - 4m = 0.
- Simplify: m2 - 2m - 15 = 0.
- Solve: (m - 5)(m + 3) = 0, so m = 5 or m = -3.
Solving Quadratic Equations by Factorisation
- Steps to solve by factorisation:
- Remove fractions and brackets if present.
- Rearrange to the form ax2 + bx + c = 0.
- Factorise the left-hand side.
- Use the Zero Product Rule: If (p)(q) = 0, then p = 0 or q = 0.
- Solve each factor to find the roots.
Example 1: Solve 2x2 - 7x = 39.
- Rearrange: 2x2 - 7x - 39 = 0.
- Factorise: 2x2 - 13x + 6x - 39 = x(2x - 13) + 3(2x - 13) = (2x - 13)(x + 3) = 0.
- Apply Zero Product Rule: 2x - 13 = 0 or x + 3 = 0.
- Solve: x = 13/2 or x = -3.
Example 2: Solve x/(x - 1) + (x - 1)/x = 5/2.
- Combine fractions: [x2 + (x - 1)2] / [x(x - 1)] = 5/2.
- Simplify numerator: x2 + x2 - 2x + 1 = 2x2 - 2x + 1.
- Cross-multiply: 2(2x2 - 2x + 1) = 5(x2 - x).
- Expand: 4x2 - 4x + 2 = 5x2 - 5x.
- Rearrange: -x2 + x + 2 = 0, or x2 - x - 2 = 0.
- Factorise: (x - 2)(x + 1) = 0.
- Solve: x = 2 or x = -1.
Solving Quadratic Equations Using the Formula
- The quadratic formula for ax2 + bx + c = 0 is:
Steps to use the formula:
- Identify a, b, and c from the equation.
- Calculate the discriminant: b2 - 4ac.
- Substitute into the formula to find x.
- Simplify the expression to get the roots.
Example 1: Solve 5x2 - 2x - 3 = 0.
- Identify: a = 5, b = -2, c = -3.
- Discriminant: (-2)2 - 4 × 5 × (-3) = 4 + 60 = 64.
- Apply formula: x = [2 ± √64] / (2 × 5) = [2 ± 8] / 10.
- Solve: x = (2 + 8)/10 = 1 or x = (2 - 8)/10 = -3/5.
Example 2: Solve x2 - 10x + 6 = 0, correct to 2 decimal places.
- Identify: a = 1, b = -10, c = 6.
- Discriminant: (-10)2 - 4 × 1 × 6 = 100 - 24 = 76.
- √76 ≈ 8.718.
- Apply formula: x = [10 ± 8.718] / 2.
- Solve: x = (10 + 8.718)/2 = 9.359 ≈ 9.36 or x = (10 - 8.718)/2 = 0.641 ≈ 0.64.
Equations Reducible to Quadratic Equations
- Some equations can be transformed into quadratic equations by substitution.
- Identify a substitution that simplifies the equation to ax2 + bx + c = 0.
- Solve the resulting quadratic equation.
- Back-substitute to find the original variable.
Example 1: Solve 2x4 - 5x2 + 3 = 0.
- Substitute y = x2, so 2y2 - 5y + 3 = 0.
- Factorise: (y - 1)(2y - 3) = 0.
- Solve: y = 1 or y = 3/2.
- Back-substitute: If y = 1, x2 = 1, x = ±1.
- If y = 3/2, x2 = 3/2, x = ±√(3/2) = ±√6/2.
Example 2: Solve √(x/(1 - x)) + √((1 - x)/x) = 13/6, x ≠ 0, x ≠ 1.
- Let √(x/(1 - x)) = y, so √((1 - x)/x) = 1/y.
- Equation becomes: y + 1/y = 13/6.
- Multiply through by y: y2 + 1 = (13/6)y.
- Rearrange: 6y2 - 13y + 6 = 0.
- Factorise: (2y - 3)(3y - 2) = 0, so y = 3/2 or y = 2/3.
- For y = 3/2: √(x/(1 - x)) = 3/2, so x/(1 - x) = 9/4, solve to get x = 9/13.
- For y = 2/3: √(x/(1 - x)) = 2/3, so x/(1 - x) = 4/9, solve to get x = 4/13.
The document Quadratic Equations Chapter Notes | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|198 docs|30 tests
|
FAQs on Quadratic Equations Chapter Notes - Mathematics Class 10 ICSE
| 1. What are the different methods to solve quadratic equations? |  |
Ans. Quadratic equations can be solved using several methods, including factorization, completing the square, and the quadratic formula. Factorization involves expressing the equation in a product form, while completing the square rewrites it in a perfect square format. The quadratic formula, x = (-b ± √(b² - 4ac)) / 2a, is a universal method applicable to all quadratic equations.
| 2. How can we examine the nature of the roots of a quadratic equation? | |
Ans. The nature of the roots of a quadratic equation can be determined using the discriminant, which is given by the expression b² - 4ac. If the discriminant is positive, the equation has two distinct real roots. If it is zero, there is one real root (a repeated root). If the discriminant is negative, the roots are complex and not real.
| 3. What is the significance of the quadratic formula in solving equations? | |
Ans. The quadratic formula is significant because it provides a reliable method to find the roots of any quadratic equation, regardless of whether it can be factored easily. This formula ensures that all possible roots (real or complex) can be calculated, making it a powerful tool in algebra.
| 4. What are equations reducible to quadratic equations, and how can they be solved? | |
Ans. Equations reducible to quadratic equations are those that can be transformed into a standard quadratic form, often through substitution or rearrangement. For example, equations involving variables raised to higher powers or certain polynomial forms can be simplified into a quadratic equation, allowing the use of standard solving techniques.
| 5. Why is factorization an important method for solving quadratic equations? | |
Ans. Factorization is important because it allows for a straightforward way to solve quadratic equations, especially when the roots are rational numbers. It simplifies the process of finding the roots by breaking down the quadratic into simpler binomials, making it easier to analyze and understand the behavior of the equation.
About this Document
4.68/5
Rating
Oct 11, 2025
Last updated
Document Description: Chapter Notes: Quadratic Equations for Class 10 2025 is part of Mathematics Class 10 ICSE preparation.
The notes and questions for Chapter Notes: Quadratic Equations have been prepared according to the Class 10 exam syllabus. Information about Chapter Notes: Quadratic Equations covers topics
like Introduction, To Examine the Nature of the Roots, Solving Quadratic Equations by Factorisation, Solving Quadratic Equations Using the Formula, Equations Reducible to Quadratic Equations and Chapter Notes: Quadratic Equations Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Quadratic Equations.
Introduction of Chapter Notes: Quadratic Equations in English is available as part of our Mathematics Class 10 ICSE
for Class 10 & Chapter Notes: Quadratic Equations in Hindi for Mathematics Class 10 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Quadratic Equations Chapter Notes | Mathematics Class 10 ICSE
Description
Full syllabus notes, lecture & questions for Quadratic Equations Chapter Notes | Mathematics Class 10 ICSE - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 10 ICSE | Best notes, free PDF download
Information about Chapter Notes: Quadratic Equations
In this doc you can find the meaning of Chapter Notes: Quadratic Equations defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Quadratic Equations theory, EduRev gives you an ample number of questions to practice Chapter Notes: Quadratic Equations tests, examples and also practice Class 10
tests
Related Searches
Important questions
,past year papers
,Quadratic Equations Chapter Notes | Mathematics Class 10 ICSE
,Quadratic Equations Chapter Notes | Mathematics Class 10 ICSE
,MCQs
,Quadratic Equations Chapter Notes | Mathematics Class 10 ICSE
,Previous Year Questions with Solutions
,Sample Paper
,Exam
,shortcuts and tricks
,study material
,Summary
,Extra Questions
,mock tests for examination
,ppt
,Free
,practice quizzes
,Viva Questions
,Semester Notes
,Objective type Questions
,video lectures
;
Additional Information about Chapter Notes: Quadratic Equations for Class 10 Preparation
Chapter Notes: Quadratic Equations Free PDF Download
The Chapter Notes: Quadratic Equations is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Quadratic Equations now and kickstart your journey towards success in the Class 10 exam.
Importance of Chapter Notes: Quadratic Equations
The importance of Chapter Notes: Quadratic Equations cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Quadratic Equations
Chapter Notes: Quadratic Equations Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Quadratic Equations.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Quadratic Equations Notes on EduRev are your ultimate resource for success.
Chapter Notes: Quadratic Equations Class 10 Questions
The "Chapter Notes: Quadratic Equations Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Quadratic Equations on the App
Students of Class 10 can study Chapter Notes: Quadratic Equations alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Quadratic Equations,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Quadratic Equations is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup