Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Chapter Notes: Remainder and Factor Theorems
Remainder and Factor Theorems Chapter Notes | Mathematics Class 10 ICSE PDF Download
| Table of contents |
|
| Introduction |
|
| A Basic Concept |
|
| Remainder Theorem |
|
| Factor Theorem |
|
| Using the Factor Theorem to Factorise the Given Polynomial |
|
Introduction
Dive into the fascinating world of polynomials with the Remainder and Factor Theorems, the superheroes of algebra in your Class 10 ICSE Mathematics journey! These theorems are like magic keys that unlock the secrets of polynomial division, helping you find remainders without tedious calculations and identify factors with ease. Imagine simplifying complex polynomial puzzles into neat, solvable pieces—this chapter equips you with the tools to do just that. Whether you're determining if a polynomial is divisible by a linear expression or breaking it down into its factors, these concepts make algebra both exciting and approachable. Get ready to explore a chapter that transforms the way you see polynomials!
A Basic Concept
- A polynomial f(x) is a function where the value of f(x) depends on the variable x.
- Substituting different values of x into the polynomial changes the output of f(x).
- Dividing a polynomial f(x) by a linear expression like x - a may leave a remainder.
Example: Find the remainder when f(x) = x2- 5x + 8 is divided by x - 2.
- Or we can substitute x = 2 into f(x).
- f(2) = 22 - 5 × 2 + 8 = 4 - 10 + 8 = 2.
- Remainder = 2.
Remainder Theorem
- Theorem: If a polynomial f(x) is divided by x - a, the remainder is f(a).
- Steps to find the remainder:
- Set the divisor x - a = 0 to find x = a.
- Substitute x = a into f(x) to compute f(a).
- The value of f(a) is the remainder.
Example: Find the remainder when x2- 8x + 4 is divided by 2x + 1.
- Set 2x + 1 = 0 → x = -1/2.
- Substitute x = -1/2 into f(x) = x2 - 8x + 4.
- f(-1/2) = (-1/2)2 - 8 × (-1/2) + 4 = 1/4 + 4 + 4 = 33/4.
- Remainder = 33/4.
Solved Example: Find the value of 'a' if ax3 + 9x2+ 4x - 10 divided by x + 3 leaves a remainder of 5.
- Set x + 3 = 0 → x = -3.
- Given remainder = 5, so f(-3) = 5.
- f(x) = ax3 + 9x2 + 4x - 10.
- f(-3) = a(-3)3 + 9(-3)2 + 4(-3) - 10 = -27a + 81 - 12 - 10 = 5.
- -27a + 59 = 5 → -27a = -54 → a = 2.
- Answer: a = 2.
Factor Theorem
- Theorem: If f(a) = 0 when a polynomial f(x) is divided by x - a, then x - a is a factor of f(x).
- Conversely, if x - a is a factor, then f(a) = 0.
- Steps to check if x - a is a factor:
- Compute f(a).
- If f(a) = 0, then x - a is a factor.
Example 1: Determine whether x - 1 is a factor of x6 - x5 + x4 + x3 - x2- x + 1.
- Set x - 1 = 0 → x = 1.
- Substitute x = 1: f(1) = 16 - 15 + 14 + 13 - 12 - 1 + 1 = 1 - 1 + 1 + 1 - 1 - 1 + 1 = 1.
- Since f(1) ≠ 0, x - 1 is not a factor.
Example 2: Find the value of 'k' if x - 2 is a factor of x3 + 2x2- kx + 10. Check if x + 5 is also a factor.
- Set x - 2 = 0 → x = 2.
- Since x - 2 is a factor, f(2) = 0.
- f(x) = x3 + 2x2 - kx + 10.
- f(2) = 23 + 2(2)2 - k(2) + 10 = 8 + 8 - 2k + 10 = 26 - 2k = 0.
- 2k = 26 → k = 13.
- Polynomial becomes x3 + 2x2 - 13x + 10.
- Check x + 5: Set x + 5 = 0 → x = -5.
- f(-5) = (-5)3 + 2(-5)2 - 13(-5) + 10 = -125 + 50 + 65 + 10 = 0.
- Since f(-5) = 0, x + 5 is a factor.
- Answer: k = 13, x + 5 is a factor.
Using the Factor Theorem to Factorise the Given Polynomial
- If f(a) = 0, then x - a is a factor of f(x).
- After finding one factor, divide f(x) by x - a to get a quotient polynomial.
- Factorise the quotient further if possible to completely factorise f(x).
- Steps to factorise:
- Find a value 'a' such that f(a) = 0.
- Divide f(x) by x - a to get the quotient.
- Factorise the quotient polynomial.
Example 1: Show that x - 2 is a factor of 3x2- 5x - 2 and factorise completely.
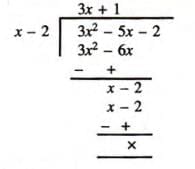
- Set x - 2 = 0 → x = 2.
- f(x) = 3x2 - 5x - 2.
- f(2) = 3(2)2 - 5(2) - 2 = 12 - 10 - 2 = 0.
- Since f(2) = 0, x - 2 is a factor.
- Divide 3x2 - 5x - 2 by x - 2:
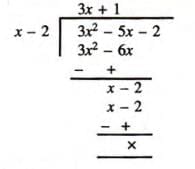
- Quotient = 3x + 1.
- Thus, 3x2 - 5x - 2 = (x - 2)(3x + 1).
Example 2: Factorise 2x3 + x2- 13x + 6 completely using the Remainder Theorem.
- Test possible factors (factors of 6): x = ±1, ±2, ±3, ±6.
- Try x = 1: f(1) = 2(1)3 + 12 - 13(1) + 6 = 2 + 1 - 13 + 6 = -4 ≠ 0.
- Try x = 2: f(2) = 2(2)3 + 22 - 13(2) + 6 = 16 + 4 - 26 + 6 = 0.
- x - 2 is a factor.
- Divide 2x3 + x2 - 13x + 6 by x - 2: Quotient = 2x2 + 5x - 3.
- Factorise 2x2 + 5x - 3 = (2x - 1)(x + 3).
- Thus, 2x3 + x2 - 13x + 6 = (x - 2)(2x - 1)(x + 3).
The document Remainder and Factor Theorems Chapter Notes | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|213 docs|30 tests
|
FAQs on Remainder and Factor Theorems Chapter Notes - Mathematics Class 10 ICSE
| 1. What is the Remainder Theorem and how is it used in polynomial division? |  |
Ans. The Remainder Theorem states that if a polynomial f(x) is divided by a linear divisor of the form (x - c), the remainder of this division is equal to f(c). This means you can find the remainder by simply substituting the value c into the polynomial. This theorem is useful for quickly determining the value of a polynomial at a specific point without performing the entire division.
| 2. Can you explain the Factor Theorem and its significance in polynomial factorization? | |
Ans. The Factor Theorem is an extension of the Remainder Theorem that states a polynomial f(x) has a factor (x - c) if and only if f(c) = 0. This is significant because it allows us to identify factors of polynomials by finding their roots. If we can find a value c that makes f(c) = 0, we can use (x - c) as a factor and further factor the polynomial.
| 3. How can I use the Factor Theorem to factorize a given polynomial? | |
Ans. To factor a polynomial using the Factor Theorem, follow these steps: First, identify potential roots by testing possible values of c. Substitute these values into the polynomial until you find one that results in f(c) = 0. Once a root is found, you can use polynomial long division or synthetic division to divide the original polynomial by (x - c), resulting in a simpler polynomial. Repeat this process with the quotient until the polynomial is completely factored.
| 4. What are some common mistakes students make when applying the Remainder and Factor Theorems? | |
Ans. Common mistakes include incorrectly substituting values into the polynomial, misunderstanding the relationship between remainders and factors, and failing to check all possible roots. Students may also forget to confirm that a polynomial is completely factored or misinterpret the results from synthetic division. Careful attention to detail and step-by-step verification can help avoid these pitfalls.
| 5. How are the Remainder and Factor Theorems applied in real-world scenarios? | |
Ans. The Remainder and Factor Theorems are applied in various fields such as engineering, computer science, and economics, where polynomial equations model real-world situations. For example, they can be used to analyze data trends, optimize functions, and solve problems involving rates of change. Understanding these theorems allows professionals to efficiently find solutions or simplify complex calculations in their respective fields.
About this Document
4.74/5
Rating
Sep 28, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Remainder and Factor Theorems for Class 10 2025 is part of Mathematics Class 10 ICSE preparation.
The notes and questions for Chapter Notes: Remainder and Factor Theorems have been prepared according to the Class 10 exam syllabus. Information about Chapter Notes: Remainder and Factor Theorems covers topics
like Introduction, A Basic Concept, Remainder Theorem, Factor Theorem, Using the Factor Theorem to Factorise the Given Polynomial and Chapter Notes: Remainder and Factor Theorems Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Remainder and Factor Theorems.
Introduction of Chapter Notes: Remainder and Factor Theorems in English is available as part of our Mathematics Class 10 ICSE
for Class 10 & Chapter Notes: Remainder and Factor Theorems in Hindi for Mathematics Class 10 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Remainder and Factor Theorems Chapter Notes | Mathematics Class 10 ICSE
Description
Full syllabus notes, lecture & questions for Remainder and Factor Theorems Chapter Notes | Mathematics Class 10 ICSE - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 10 ICSE | Best notes, free PDF download
Information about Chapter Notes: Remainder and Factor Theorems
In this doc you can find the meaning of Chapter Notes: Remainder and Factor Theorems defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Remainder and Factor Theorems theory, EduRev gives you an ample number of questions to practice Chapter Notes: Remainder and Factor Theorems tests, examples and also practice Class 10
tests
Related Searches
Remainder and Factor Theorems Chapter Notes | Mathematics Class 10 ICSE
,Exam
,practice quizzes
,ppt
,video lectures
,study material
,Free
,Previous Year Questions with Solutions
,Remainder and Factor Theorems Chapter Notes | Mathematics Class 10 ICSE
,Sample Paper
,shortcuts and tricks
,Objective type Questions
,MCQs
,Viva Questions
,Semester Notes
,Summary
,past year papers
,Important questions
,Extra Questions
,mock tests for examination
,Remainder and Factor Theorems Chapter Notes | Mathematics Class 10 ICSE
;
Additional Information about Chapter Notes: Remainder and Factor Theorems for Class 10 Preparation
Chapter Notes: Remainder and Factor Theorems Free PDF Download
The Chapter Notes: Remainder and Factor Theorems is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Remainder and Factor Theorems now and kickstart your journey towards success in the Class 10 exam.
Importance of Chapter Notes: Remainder and Factor Theorems
The importance of Chapter Notes: Remainder and Factor Theorems cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Remainder and Factor Theorems
Chapter Notes: Remainder and Factor Theorems Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Remainder and Factor Theorems.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Remainder and Factor Theorems Notes on EduRev are your ultimate resource for success.
Chapter Notes: Remainder and Factor Theorems Class 10 Questions
The "Chapter Notes: Remainder and Factor Theorems Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Remainder and Factor Theorems on the App
Students of Class 10 can study Chapter Notes: Remainder and Factor Theorems alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Remainder and Factor Theorems,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Remainder and Factor Theorems is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup