Open App

Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Chapter Notes: Similarity

Similarity Chapter Notes | Mathematics Class 10 ICSE PDF Download

Q: 1. What are similar triangles and how can they be identified?

Ans. Similar triangles are triangles that have the same shape but may differ in size. They can be identified by their corresponding angles being equal and the lengths of their corresponding sides being proportional. The common criteria to establish similarity include Angle-Angle (AA), Side-Angle-Side (SAS), and Side-Side-Side (SSS).

Q: 2. What is the Basic Proportionality Theorem and how can it be applied?

Ans. The Basic Proportionality Theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. This theorem can be applied in various real-life problems such as finding distances in maps or scaling models, where maintaining proportional relationships is crucial.

Q: 3. How does similarity relate to the areas of two triangles?

Ans. The areas of two similar triangles are proportional to the squares of the lengths of their corresponding sides. If the ratio of the lengths of corresponding sides of two similar triangles is a:b, then the ratio of their areas will be a²:b². This relationship helps in solving problems involving area calculations in similar figures.

Q: 4. Can you explain the concept of similarity as a size transformation?

Ans. Similarity as a size transformation refers to scaling a shape while maintaining its proportions. When a shape is enlarged or reduced but retains its angles and the ratios of its sides, it is said to undergo a size transformation. This concept is fundamental in geometry and is applied in various fields, including architecture and engineering.

Q: 5. How are similar triangles used in real-world applications, such as maps and models?

Ans. Similar triangles are utilized in maps and models to represent real-world distances and dimensions accurately while maintaining proportionality. For example, the scale on a map allows users to convert distances on the map to actual distances on the ground, preserving the similarity between the triangles formed by the map and the real-world scenario.

Table of contents
Introduction
Similar Triangles
Corresponding Sides and Corresponding Angles
Condition of Similar Triangle (SAS, AA or AAA and SSS)
Basic Proportionality Theorem with Applications
Relation Between the Areas of Two Triangles
Similarity as a Size Transformation
Applications to Maps and Models
Solved Examples

Chapter 15: Similarity (With Applications to Maps and Models) Notes

Introduction

Imagine looking at a map of your country or a tiny model of a grand building—both are smaller versions of the real thing, yet they look exactly the same in shape! This fascinating concept is called similarity, a key idea in geometry that helps us understand how shapes can be alike even if their sizes differ. In this chapter, we’ll explore how figures like triangles can be similar, how their sides and angles relate, and how this idea applies to everyday things like maps and models. Get ready to dive into the world of proportional shapes and size transformations, and see how math connects to the real world in exciting ways!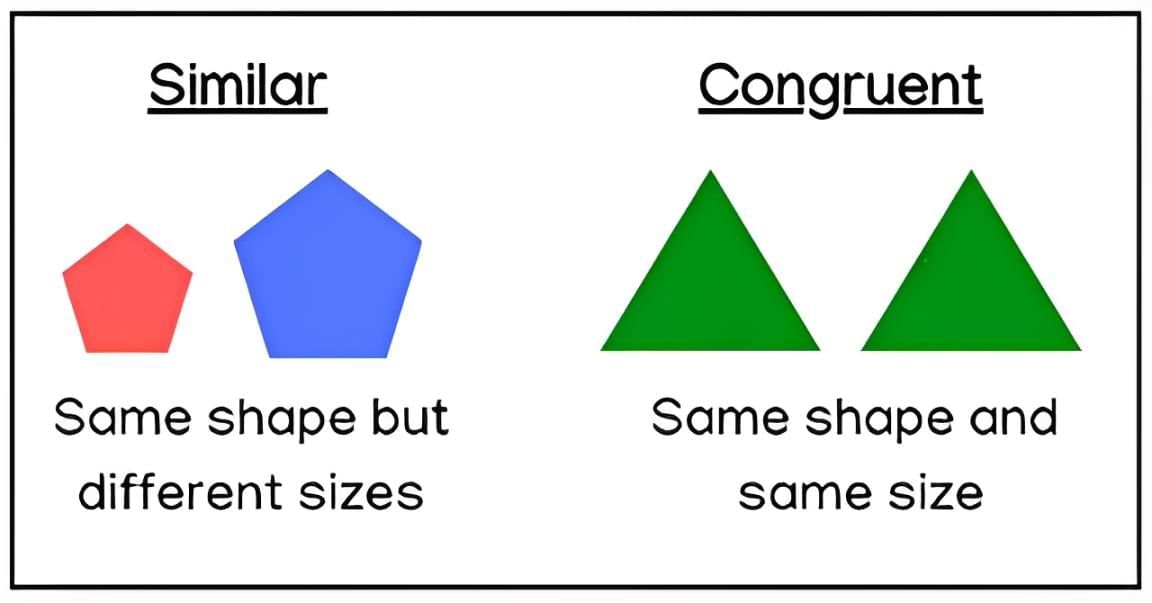 Similarity Chapter Notes | Mathematics Class 10 ICSE

Similarity in geometry means two figures have the same shape but can be different in size.
Steps to understand similarity:
- Identify the shape: Check if two figures look alike in their form.
- Compare angles: For figures to be similar, their angles must be equal.
- Check sizes: Sizes may differ, but the shape remains the same.
Congruency means two figures have both the same shape and the same size.
Steps to understand congruency:
- Match shapes: Ensure the figures have identical forms.
- Measure sides: All sides of one figure must equal the sides of the other.
- Confirm angles: All angles must be equal too.
Congruent figures are always similar, but similar figures are not always congruent.

Similar Triangles

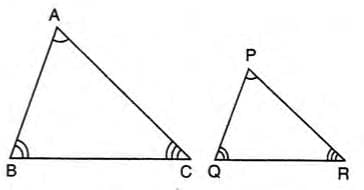
Similarity Chapter Notes | Mathematics Class 10 ICSE

Two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional.
Steps to check for similar triangles:
- Measure angles: Ensure each angle in one triangle equals the corresponding angle in the other.
- Compare sides: Calculate the ratios of corresponding sides; they must be equal.
Conditions for similarity:
- Corresponding angles are equal: Angle A = Angle P, Angle B = Angle Q, Angle C = Angle R.
- Corresponding sides are proportional: AB/PQ = BC/QR = AC/PR.
Notation: We write ΔABC ~ ΔPQR to show triangle ABC is similar to triangle PQR.
Example: In triangles ABC and PQR, if Angle A = Angle P, Angle B = Angle Q, Angle C = Angle R, and AB/PQ = BC/QR = AC/PR, then ΔABC ~ ΔPQR.

Corresponding Sides and Corresponding Angles

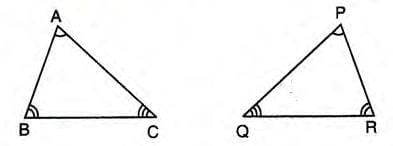
Similarity Chapter Notes | Mathematics Class 10 ICSE

In similar triangles, sides opposite to equal angles are called corresponding sides.
Steps to identify corresponding sides:
- Find equal angles: Locate angles that are the same in both triangles.
- Identify opposite sides: The sides opposite these equal angles are corresponding.
Example: In ΔABC ~ ΔPRQ, if Angle A = Angle P, then sides BC and QR (opposite to Angle A and Angle P) are corresponding sides.
Formula: For similar triangles ABC and PRQ, BC/QR = AC/PQ = AB/PR.
In similar triangles, angles opposite to proportional sides are corresponding angles and are equal.
Steps to identify corresponding angles:
- Check side ratios: Find the ratios of corresponding sides.
- Locate opposite angles: The angles opposite these proportional sides are corresponding and equal.
Example: In similar triangles ABC and EFD, if AB/EF = BC/DF = AC/DE, then Angle C (opposite AB) = Angle D (opposite EF), Angle A (opposite BC) = Angle E (opposite DF), and Angle B (opposite AC) = Angle F (opposite DE).

Condition of Similar Triangle (SAS, AA or AAA and SSS)

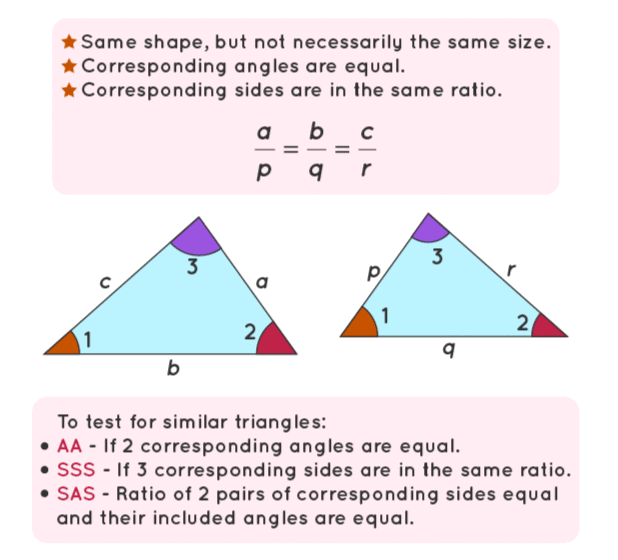
Similarity Chapter Notes | Mathematics Class 10 ICSE

Three conditions determine if two triangles are similar:

1. SAS (Side-Angle-Side): If one angle of a triangle equals an angle of another, and the sides including these angles are proportional.

Steps for SAS:
- Compare one angle: Check if one angle is equal in both triangles.
- Measure including sides: Find the lengths of the sides that form this angle.
- Check proportionality: Ensure the ratios of these sides are equal.
Example: In ΔABC and ΔDEF, if Angle A = Angle D and AB/DE = AC/DF, then ΔABC ~ ΔDEF by SAS.

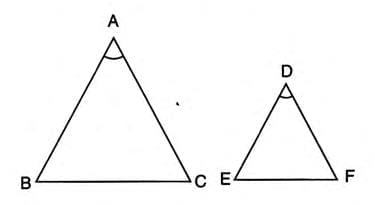
2. AA or AAA (Angle-Angle): If two angles of one triangle equal two angles of another.

Steps for AA or AAA:
- Measure two angles: Check if two angles in one triangle match two in the other.
- Third angle: Since the sum of angles in a triangle is 180°, the third angles will also be equal.
Example: In ΔABC and ΔDEF, if Angle A = Angle D and Angle B = Angle E, then ΔABC ~ ΔDEF by AA.

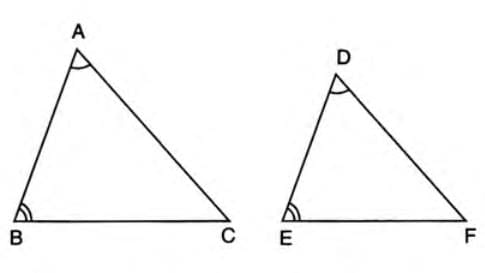
3. SSS (Side-Side-Side): If all three pairs of corresponding sides are proportional.

Steps for SSS:
- Measure all sides: Find the lengths of all sides in both triangles.
- Calculate ratios: Check if the ratios of corresponding sides are equal.
Example: In ΔABC and ΔPQR, if AB/PQ = BC/QR = AC/PR, then ΔABC ~ ΔPQR by SSS.

Basic Proportionality Theorem with Applications

Theorem 1: Basic Proportionality Theorem (BPT) or Thales' Theorem

A line drawn parallel to one side of a triangle divides the other two sides proportionally.
Given: In ΔABC, line DE is parallel to BC, with D on AB and E on AC.
To Prove: AD/DB = AE/EC.
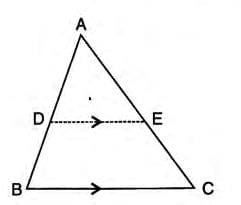
Proof:
- Statement: In ΔABC and ΔADE:
- ∠ABC = ∠ADE (Corresponding angles, since DE || BC).
- ∠ACB = ∠AED (Corresponding angles).
- ∠BAC = ∠DAE (Common angle).
- Therefore, ΔABC ~ ΔADE (AAA postulate).
- Since the triangles are similar, their corresponding sides are proportional:
- AB/AD = AC/AE (Corresponding sides of similar triangles).
- Now, AB = AD + DB and AC = AE + EC.
- Substitute: (AD + DB)/AD = (AE + EC)/AE.
- Rewrite: (AD/AD) + (DB/AD) = (AE/AE) + (EC/AE).
- Simplify: 1 + (DB/AD) = 1 + (EC/AE).
- Subtract 1: DB/AD = EC/AE.
- Take reciprocals: AD/DB = AE/EC.
- Hence proved.
Converse: If a line divides any two sides of a triangle proportionally, the line is parallel to the third side.
Given: In ΔABC, D and E are points on AB and AC such that AD/DB = AE/EC.
To Prove: DE || BC.
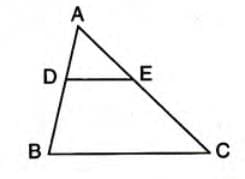
Proof:
- Assume DE is not parallel to BC.
- Draw DF || BC, where F is a point on AC.
- By BPT in ΔABC with DF || BC: AD/DB = AF/FC.
- Given: AD/DB = AE/EC.
- So, AF/FC = AE/EC.
- Rewrite: AF/FC = AE/EC implies (AF/AE) = (FC/EC).
- Add 1: (AF/AE) + 1 = (FC/EC) + 1.
- So, (AF + AE)/AE = (FC + EC)/EC.
- Since AC = AE + EC, we get: (AF + AE)/AE = AC/EC.
- Similarly, (AF + AE)/AE = AC/AE.
- Thus, AC/EC = AC/AE, which implies EC = AE, a contradiction unless E and F coincide.
- Therefore, DE || BC.

Example: In ΔABC, DE || BC, AD/DB = 2/3, and BC = 7.5 cm. Find DE.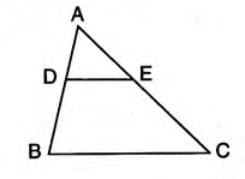 Similarity Chapter Notes | Mathematics Class 10 ICSE Solution:

By BPT: AD/DB = AE/EC.
Also, since ΔADE ~ ΔABC (by AA), AD/AB = DE/BC.
Given: AD/DB = 2/3, so AD/DB = 2/3 implies AD/(AD + DB) = 2/(2 + 3) = 2/5.
Since AB = AD + DB, we have AD/AB = 2/5.
Thus, DE/BC = AD/AB = 2/5.
So, DE/7.5 = 2/5.
DE = (2/5) × 7.5 = 3 cm.

Relation Between the Areas of Two Triangles

Theorem 2: Area Ratio Theorem for Similar Triangles

The corresponding sides of similar triangles are proportional to the squares of their areas.
Given: ΔABC ~ ΔDEF, such that ∠B = ∠E and ∠C = ∠F.
To Prove: (Area of ΔABC)/(Area of ΔDEF) = (AB/DE)² = (BC/EF)² = (AC/DF)².
Construction: Draw AM ⊥ BC and DN ⊥ EF.
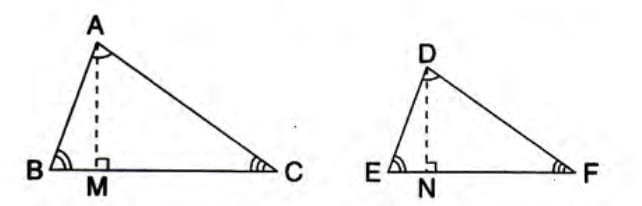
Proof:
- Area of ΔABC = (1/2) × BC × AM.
- Area of ΔDEF = (1/2) × EF × DN.
- So, (Area of ΔABC)/(Area of ΔDEF) = [(1/2) × BC × AM]/[(1/2) × EF × DN] = (BC/EF) × (AM/DN).
- In ΔABM and ΔDEN:
- ∠AMB = ∠DNE (Each 90°, since AM ⊥ BC and DN ⊥ EF).
- ∠B = ∠E (Given, since ΔABC ~ ΔDEF).
- Thus, ΔABM ~ ΔDEN (AA postulate).
- So, AM/DN = AB/DE (Corresponding sides of similar triangles).
- Substitute: (Area of ΔABC)/(Area of ΔDEF) = (BC/EF) × (AM/DN) = (BC/EF) × (AB/DE).
- Since ΔABC ~ ΔDEF, AB/DE = BC/EF = AC/DF.
- Thus, (Area of ΔABC)/(Area of ΔDEF) = (BC/EF) × (AB/DE) = (AB/DE) × (AB/DE) = (AB/DE)².
- Similarly, it equals (BC/EF)² and (AC/DF)².
- Hence proved.
Remark: If two triangles share a common vertex and their bases are along the same straight line, the ratio of their areas equals the ratio of their bases.

Example: In ΔABC, D and E are points on AB and AC such that DE || BC. Find the ratio of areas of ΔADE to ΔABC.
Solution: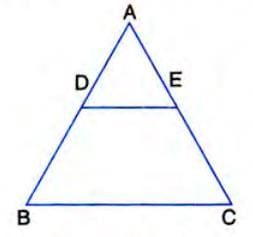

Since DE || BC, by BPT: AD/DB = AE/EC.
Also, ΔADE ~ ΔABC (by AA, since ∠A is common and ∠ADE = ∠ABC).
By the area ratio theorem: (Area of ΔADE)/(Area of ΔABC) = (AD/AB)².
Since AB = AD + DB, we need AD/AB, which depends on the specific ratio AD/DB (can be computed if given).

Similarity as a Size Transformation

Similarity can be seen as a size transformation, where a figure is enlarged or reduced by a scale factor k.
Steps for size transformation:
- Choose a point: Select a center of enlargement or reduction (e.g., point P).
- Scale the distances: Multiply the distance from P to each vertex by the scale factor k.
- Join new points: Connect the new points to form the transformed figure.
Enlargement: If k > 1, the figure gets bigger.
Example: For triangle ABC, mark point P outside. Join P to A, B, C.
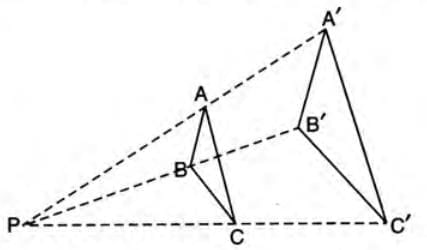Produce PA to A' such that PA' = 2 × PA, PB to B' such that PB' = 2 × PB, and PC to C' such that PC' = 2 × PC. Join A', B', C' to get ΔA'B'C' ~ ΔABC, with A'B' = 2 × AB, B'C' = 2 × BC, C'A' = 2 × CA (scale factor k = 2).
Reduction: If k < 1, the figure gets smaller.
Example: For triangle ABC and point P, take A' in PA such that PA' = 1/2 × PA, B' in PB such that PB' = 1/2 × PB, and C' in PC such that PC' = 1/2 × PC.
Join A', B', C' to get ΔA'B'C' ~ ΔABC, with A'B' = 1/2 × AB, B'C' = 1/2 × BC, C'A' = 1/2 × CA (scale factor k = 1/2).
Properties of size transformation:
- The image of a line is a line.
- The image of a triangle is a triangle.
- The image of a quadrilateral is a quadrilateral, and so on.

Applications to Maps and Models

Similarity is used in maps and models to represent real objects at a smaller or larger scale.
Steps to understand maps:
- Measure distances: Find the distance between two points on the map.
- Compare to actual: Compare this to the real distance between the points.
- Find the scale: The ratio of map distance to actual distance is the scale factor k.
Example: On a map of India, if the scale is 1:20,000, then 1 cm on the map equals 20,000 cm (0.2 km) on the ground.
Scale factor (k): The ratio written on maps, e.g., 1:20,000, means k = 1/20,000.
Steps for models:
- Understand the object: Know the dimensions of the real object.
- Apply scale factor: Use k to find the model’s dimensions (multiply real dimensions by k for reduction, or divide model dimensions by k for actual size).
- Calculate properties: Use k for lengths, k² for areas, and k³ for volumes.
Formulas for maps and models:
- Length of model = k × length of actual object.
- Area of model = k² × area of actual object.
- Volume of model = k³ × volume of actual object.

Solved Examples

Example 1: Right-Angled Triangle and Altitude
Problem: In triangle ABC, right-angled at A, AD is perpendicular to BC. Prove ΔDBA ~ ΔDAC ~ ΔABC.
Solution: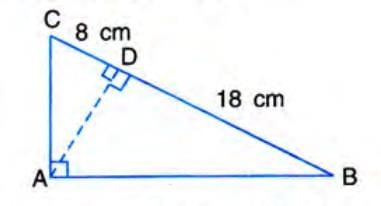

In ΔDBA and ΔABC:
- Angle ABD = Angle ABC (common).
- Angle ADB = Angle BAC (each 90°).
- Thus, ΔDBA ~ ΔABC by AA postulate.
In ΔDAC and ΔABC:
- Angle ACD = Angle ACB (common).
- Angle ADC = Angle BAC (each 90°).
- Thus, ΔDAC ~ ΔABC by AA postulate.
Conclusion: ΔDBA ~ ΔDAC ~ ΔABC.

Example 2: Parallel Lines and Transversals
Problem: Lines l and m are parallel. Three concurrent lines through point O meet l at A, B, C and m at P, Q, R. Prove AB/BC = QR/PQ.
Solution:
Since l || m and AR is a transversal:

Angle OAB = Angle ORQ (alternate angles).
Angle AOB = Angle QOR (vertically opposite angles).
Thus, ΔOAB ~ ΔORQ by AA postulate.
So, AB/QR = OB/OQ (corresponding sides are proportional).

Similarly, for l || m and transversal:

Angle OCB = Angle OPQ (alternate angles).
Angle BOC = Angle POQ (vertically opposite angles).
Thus, ΔBOC ~ ΔQOP by AA postulate.
So, BC/PQ = OB/OQ (corresponding sides are proportional).

From both, AB/QR = BC/PQ, hence AB/BC = QR/PQ.

Example 3: Model of a Tank
Problem: A rectangular tank has length = 4 m, width = 3 m, capacity = 30 m³. A model has capacity 240 cm³. Find (i) dimensions of the model, (ii) ratio of total surface area of tank to model.
Solution:
Step 1: Find height of tank.

Volume = length × breadth × height.
30 m³ = 4 m × 3 m × height.
Height = 30 / (4 × 3) = 2.5 m.

Step 2: Find scale factor k.

Volume of model = k³ × volume of tank.
240 cm³ = k³ × 30 m³.
Convert units: 30 m³ = 30 × 100 × 100 × 100 cm³.
So, 240 = k³ × 30 × 100 × 100 × 100.
k³ = 240 / (30 × 100 × 100 × 100) = 1/125000.
Scale factor k = 1/50.
(i) Dimensions of the model:
- Length of model = k × length of tank = 1/50 × 4 m = 8 cm.
- Breadth of model = k × breadth of tank = 1/50 × 3 m = 6 cm.
- Height of model = k × height of tank = 1/50 × 2.5 m = 5 cm.
- Dimensions = 8 cm × 6 cm × 5 cm.
(ii) Ratio of total surface areas:
- Total surface area of model = k² × total surface area of tank.
- So, total S.A. of tank / total S.A. of model = 1/k².
- = 1/(1/50)² = 50² = 2500.
- Ratio = 2500:1.

The document Similarity Chapter Notes | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.

All you need of Class 10 at this link: Class 10

	Mathematics Class 10 ICSE 74 videos\|198 docs\|30 tests

Mathematics Class 10 ICSE

74 videos|198 docs|30 tests

Join Course for Free

FAQs on Similarity Chapter Notes - Mathematics Class 10 ICSE

1. What are similar triangles and how can they be identified?

Ans. Similar triangles are triangles that have the same shape but may differ in size. They can be identified by their corresponding angles being equal and the lengths of their corresponding sides being proportional. The common criteria to establish similarity include Angle-Angle (AA), Side-Angle-Side (SAS), and Side-Side-Side (SSS).

2. What is the Basic Proportionality Theorem and how can it be applied?

Ans. The Basic Proportionality Theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. This theorem can be applied in various real-life problems such as finding distances in maps or scaling models, where maintaining proportional relationships is crucial.

3. How does similarity relate to the areas of two triangles?

Ans. The areas of two similar triangles are proportional to the squares of the lengths of their corresponding sides. If the ratio of the lengths of corresponding sides of two similar triangles is a:b, then the ratio of their areas will be a²:b². This relationship helps in solving problems involving area calculations in similar figures.

4. Can you explain the concept of similarity as a size transformation?

Ans. Similarity as a size transformation refers to scaling a shape while maintaining its proportions. When a shape is enlarged or reduced but retains its angles and the ratios of its sides, it is said to undergo a size transformation. This concept is fundamental in geometry and is applied in various fields, including architecture and engineering.

5. How are similar triangles used in real-world applications, such as maps and models?

Ans. Similar triangles are utilized in maps and models to represent real-world distances and dimensions accurately while maintaining proportionality. For example, the scale on a map allows users to convert distances on the map to actual distances on the ground, preserving the similarity between the triangles formed by the map and the real-world scenario.

About this Document

4.97/5 Rating

Sep 28, 2025 Last updated

Related Exams

Class 10

Document Description: Chapter Notes: Similarity for Class 10 2025 is part of Mathematics Class 10 ICSE preparation. The notes and questions for Chapter Notes: Similarity have been prepared according to the Class 10 exam syllabus. Information about Chapter Notes: Similarity covers topics like Introduction, Similar Triangles, Corresponding Sides and Corresponding Angles, Condition of Similar Triangle (SAS, AA or AAA and SSS), Basic Proportionality Theorem with Applications, Relation Between the Areas of Two Triangles, Similarity as a Size Transformation, Applications to Maps and Models, Solved Examples and Chapter Notes: Similarity Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Similarity.

Introduction of Chapter Notes: Similarity in English is available as part of our Mathematics Class 10 ICSE for Class 10 & Chapter Notes: Similarity in Hindi for Mathematics Class 10 ICSE course. Download more important topics related with notes, lectures and mock test series for Class 10 Exam by signing up for free. Class 10: Similarity Chapter Notes | Mathematics Class 10 ICSE

Description

Full syllabus notes, lecture & questions for Similarity Chapter Notes | Mathematics Class 10 ICSE - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 10 ICSE | Best notes, free PDF download

Information about Chapter Notes: Similarity

In this doc you can find the meaning of Chapter Notes: Similarity defined & explained in the simplest way possible. Besides explaining types of Chapter Notes: Similarity theory, EduRev gives you an ample number of questions to practice Chapter Notes: Similarity tests, examples and also practice Class 10 tests

	Mathematics Class 10 ICSE 74 videos\|198 docs\|30 tests

Mathematics Class 10 ICSE

74 videos|198 docs|30 tests

Join Course for Free

Download as PDF

Explore Courses for Class 10 exam

Exam

shortcuts and tricks

past year papers

Extra Questions

Viva Questions

Similarity Chapter Notes | Mathematics Class 10 ICSE

MCQs

Semester Notes

ppt

pdf

video lectures

practice quizzes

Important questions

study material

Objective type Questions

Summary

Similarity Chapter Notes | Mathematics Class 10 ICSE

Free

Similarity Chapter Notes | Mathematics Class 10 ICSE

Previous Year Questions with Solutions

Sample Paper

mock tests for examination

;

Additional Information about Chapter Notes: Similarity for Class 10 Preparation

Chapter Notes: Similarity Free PDF Download

The Chapter Notes: Similarity is an invaluable resource that delves deep into the core of the Class 10 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Similarity now and kickstart your journey towards success in the Class 10 exam.

Importance of Chapter Notes: Similarity

The importance of Chapter Notes: Similarity cannot be overstated, especially for Class 10 aspirants. This document holds the key to success in the Class 10 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Chapter Notes: Similarity

Chapter Notes: Similarity Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Chapter Notes: Similarity. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Similarity Notes on EduRev are your ultimate resource for success.

Chapter Notes: Similarity Class 10 Questions

The "Chapter Notes: Similarity Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Chapter Notes: Similarity on the App

Students of Class 10 can study Chapter Notes: Similarity alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Chapter Notes: Similarity, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Chapter Notes: Similarity is prepared as per the latest Class 10 syllabus.

Education Revolution

Signup to see your scores go up
within 7 days!

Continue with Google

Takes less than 10 seconds to signup