Solving (Simple) Problems Chapter Notes - Class 10 PDF Download
Introduction
Quadratic equations are like puzzles waiting to be solved! In this exciting chapter, we dive into the world of word problems that can be cracked using quadratic equations. From finding numbers and calculating time to exploring geometric shapes and speeds, these problems help us apply math to real-life scenarios. By turning unknown quantities into variables and forming equations, we’ll unlock solutions step by step. Get ready to sharpen your problem-solving skills and discover how quadratic equations make math both fun and practical!

- Steps to solve word problems:
- Step 1: Represent the unknown quantity with a variable, e.g., 'x'.
- Step 2: Translate the problem’s statement into an equation using 'x'.
- Step 3: Solve the quadratic equation to find the value of 'x'.
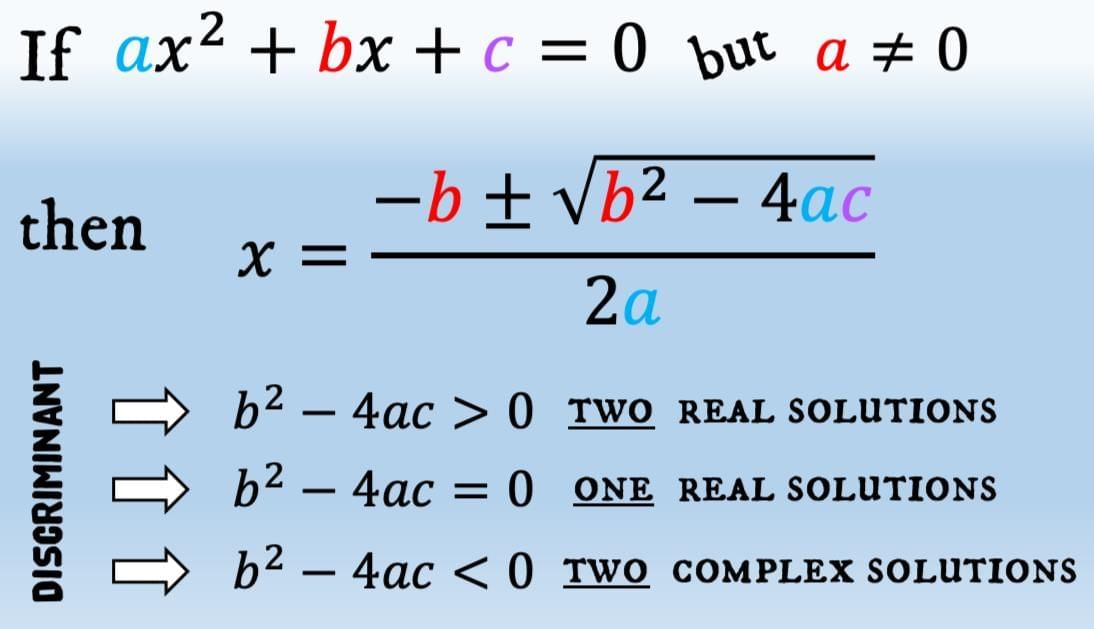
Problems Based on Numbers
Involves finding numbers (natural, whole, or others) based on conditions like their sum, difference, squares, or reciprocals.
Steps:
- Assign a variable (e.g., x) to one number.
- Express the other number in terms of x (e.g., x + 3 if they differ by 3).
- Form a quadratic equation using the given condition (e.g., sum of squares).
- Solve the equation and discard invalid solutions (e.g., negative numbers if natural numbers are required).
Example 1: Find two natural numbers that differ by 3 and whose squares sum to 117.
- Let the numbers be x and x + 3.
- Equation: x2 + (x + 3)2 = 117.
- Expand: x2 + (x2 + 6x + 9) = 117.
- Simplify: 2x2 + 6x + 9 = 117 → 2x2 + 6x - 108 = 0.
- Divide by 2: x2 + 3x - 54 = 0.
- Factorize: (x + 9)(x - 6) = 0 → x = -9 or x = 6.
- Since natural numbers are positive, discard x = -9.
- Solution: x = 6, other number = x + 3 = 9.
- Numbers are 6 and 9.
Formula: For numbers x and y, conditions like x2 + y2 = k or 1/x + 1/y = m/n lead to quadratic equations.
Example 2: Sum of two natural numbers is 8, and the difference of their reciprocals is 2/15.
- Let numbers be x and 8 - x.
- Equation: 1/x - 1/(8 - x) = 2/15.
- Simplify: (8 - x - x)/(x(8 - x)) = 2/15 → (8 - 2x)/(x(8 - x)) = 2/15.
- Cross-multiply: 15(8 - 2x) = 2x(8 - x).
- Expand: 120 - 30x = 16x - 2x2.
- Rearrange: 2x2 - 46x + 120 = 0 → x2 - 23x + 60 = 0.
- Factorize: (x - 20)(x - 3) = 0 → x = 20 or x = 3.
- Since sum is 8, discard x = 20.
- Solution: x = 3, other number = 8 - 3 = 5.
- Numbers are 3 and 5.
Problems Based on Time and Work
- Deals with finding the time taken by individuals or groups to complete a task.
- Uses the concept of work rate (work done per unit time).
- Formula: If A takes a hours and B takes b hours, their work rates are 1/a and 1/b. Together, they complete 1/(1/a + 1/b) work per hour.
- Steps:
- Assign a variable for one person’s time (e.g., x hours).
- Express the other person’s time in terms of x.
- Form an equation based on combined work rate and total time.
- Solve the quadratic equation, discarding invalid solutions (e.g., negative time).
Example 1: A takes 6 hours less than B to complete a work. Together, they finish in 13 hours 20 minutes. Find B’s time.
- Let B take x hours, so A takes x - 6 hours.
- Convert 13 hours 20 minutes = 13 + 20/60 = 40/3 hours.
- Work rates: A = 1/(x - 6), B = 1/x.
- Equation: 1/(x - 6) + 1/x = 3/40.
- Simplify: (x + x - 6)/(x(x - 6)) = 3/40 → (2x - 6)/(x(x - 6)) = 3/40.
- Cross-multiply: 40(2x - 6) = 3x(x - 6).
- Expand: 80x - 240 = 3x2 - 18x.
- Rearrange: 3x2 - 98x + 240 = 0.
- Factorize: (x - 30)(3x - 8) = 0 → x = 30 or x = 8/3.
- Discard x = 8/3 (as x - 6 would be negative).
- Solution: B takes 30 hours.
Problems Based on Geometrical Figures
- Involves applying quadratic equations to geometric shapes like triangles, rectangles, or squares.
- Commonly uses properties like Pythagoras' theorem, area, or perimeter formulas.
Formulas:
- Pythagoras' Theorem: a2 + b2 = c2 (for right triangles).
- Area of a rectangle: length × breadth.
- Perimeter of a rectangle: 2(length + breadth).
Steps:
- Assign a variable to one dimension (e.g., x for side length).
- Express other dimensions in terms of x.
- Form a quadratic equation using geometric properties.
- Solve and verify solutions (discard negative or invalid values).
Example 1: A right triangle’s hypotenuse is 13 cm, and the difference between the other two sides is 7 cm. Find the sides.
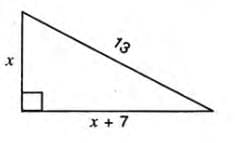
- Let shorter side = x cm, longer side = x + 7 cm.
- Pythagoras: x2 + (x + 7)2 = 132.
- Expand: x2 + (x2 + 14x + 49) = 169.
- Simplify: 2x2 + 14x + 49 = 169 → 2x2 + 14x - 120 = 0.
- Divide by 2: x2 + 7x - 60 = 0.
- Factorize: (x + 12)(x - 5) = 0 → x = -12 or x = 5.
- Discard x = -12 (side cannot be negative).
- Solution: x = 5 cm, other side = x + 7 = 12 cm.
- Sides are 5 cm and 12 cm.
Example 2: A verandah’s length is 3 m more than its breadth, and its area equals its perimeter numerically.
- Let breadth = x m, length = x + 3 m.
- Equation: Area = Perimeter → x(x + 3) = 2(x + x + 3).
- Simplify: x2 + 3x = 2(2x + 3) → x2 + 3x = 4x + 6.
- Rearrange: x2 - x - 6 = 0.
- Factorize: (x - 3)(x + 2) = 0 → x = 3 or x = -2.
- Discard x = -2 (breadth cannot be negative).
- Solution: Breadth = 3 m, length = 3 + 3 = 6 m.
Problems Based on Distance, Speed, and Time
- Focuses on problems involving distance, speed, and time relationships.
- Formula: Time = Distance / Speed.
- Steps:
- Assign a variable for speed or time (e.g., x for speed).
- Express related quantities (e.g., new speed as x + 10).
- Form a quadratic equation based on time or distance conditions.
- Solve and discard invalid solutions (e.g., negative speed).
Example 1: Increasing a car’s speed by 10 km/hr reduces the time for a 72 km journey by 36 minutes. Find the original speed.
- Let original speed = x km/hr.
- Original time = 72/x hours.
- New speed = x + 10 km/hr, new time = 72/(x + 10) hours.
- 36 minutes = 36/60 = 3/5 hours.
- Equation: 72/x - 72/(x + 10) = 3/5.
- Simplify: 72(x + 10 - x)/(x(x + 10)) = 3/5 → 720/(x(x + 10)) = 3/5.
- Cross-multiply: 3x(x + 10) = 3600.
- Expand: 3x2 + 30x - 3600 = 0 → x2 + 10x - 1200 = 0.
- Factorize: (x + 40)(x - 30) = 0 → x = -40 or x = 30.
- Discard x = -40 (speed cannot be negative).
- Solution: Original speed = 30 km/hr.
Example 2: Car A travels x km/litre, car B travels (x + 5) km/litre. Car A uses 4 litres more than car B for 400 km.
- Litres for car A = 400/x, car B = 400/(x + 5).
- Equation: 400/x - 400/(x + 5) = 4.
- Simplify: 400(x + 5 - x)/(x(x + 5)) = 4 → 2000/(x(x + 5)) = 4.
- Multiply: 4x(x + 5) = 2000 → x2 + 5x - 500 = 0.
- Factorize: (x + 25)(x - 20) = 0 → x = -25 or x = 20.
- Discard x = -25 (distance cannot be negative).
- Solution: x = 20, car B uses 400/(20 + 5) = 16 litres.
Problems on C.P. and S.P.
Involves cost price (C.P.), selling price (S.P.), profit, or loss percentages.
Formulas:
- Loss = C.P. - S.P.
- Loss% = (Loss / C.P.) × 100.
- Profit = S.P. - C.P.
- Profit% = (Profit / C.P.) × 100.
Steps:
- Assign a variable for C.P. (e.g., x).
- Express loss or profit in terms of x.
- Form a quadratic equation based on the given condition.
- Solve and verify solutions.
Example 3: Selling an article for ₹24 incurs a loss equal to the cost price percentage. Find the cost price.
- Let C.P. = ₹x.
- Loss% = x%, so loss = (x/100) × x = x2/100.
- S.P. = C.P. - Loss → 24 = x - x2/100.
- Multiply by 100: 2400 = 100x - x2.
- Rearrange: x2 - 100x + 2400 = 0.
- Factorize: (x - 60)(x - 40) = 0 → x = 60 or x = 40.
- Solution: C.P. = ₹60 or ₹40.
Miscellaneous Problems
Covers diverse problems like sums of series, digit problems, age, boats, cost, and group contributions.
Steps:
- Identify the unknown and assign a variable.
- Form a quadratic equation based on the problem’s conditions.
- Solve and discard invalid solutions.
Formulas:
- Sum of first n natural numbers: S = n(n + 1)/2.
- Time for boat downstream: Distance / (Boat speed + Stream speed).
- Time for boat upstream: Distance / (Boat speed - Stream speed).
Example 1: Find n if the sum of the first n natural numbers is 276.
- Formula: S = n(n + 1)/2 = 276.
- Equation: n(n + 1)/2 = 276 → n(n + 1) = 552.
- Rearrange: n2 + n - 552 = 0.
- Factorize: (n + 24)(n - 23) = 0 → n = -24 or n = 23.
- Discard n = -24 (n is natural).
- Solution: n = 23.
Example 2: A cloth costs ₹200. If it was 5 m longer and each metre cost ₹2 less, the total cost remains ₹200. Find the length and rate.
- Let length = x m, rate = 200/x ₹/m.
- New length = x + 5 m, new rate = 200/(x + 5) ₹/m.
- Equation: 200/x - 200/(x + 5) = 2.
- Simplify: 200(x + 5 - x)/(x(x + 5)) = 2 → 1000/(x(x + 5)) = 2.
- Multiply: 2x(x + 5) = 1000 → x2 + 5x - 500 = 0.
- Factorize: (x + 25)(x - 20) = 0 → x = -25 or x = 20.
- Discard x = -25 (length cannot be negative).
- Solution: Length = 20 m, rate = 200/20 = ₹10/m.
Alternative Method:
- New rate = (200/x - 2), new length = x + 5.
- Equation: (x + 5)(200/x - 2) = 200.
- Simplify: (x + 5)(200 - 2x)/x = 200.
- Multiply: 200x - 2x2 + 1000 - 10x = 200x.
- Rearrange: 2x2 - 10x - 1000 = 0 → x2 + 5x - 500 = 0.
- Same solution: x = 20, length = 20 m, rate = ₹10/m.
Example 3: A shopkeeper buys books for ₹960. If each book cost ₹8 less, he could buy 4 more books. Find the original cost per book.
- Let cost per book = ₹x, number of books = 960/x.
- New cost = x - 8, new number = 960/(x - 8).
- Equation: 960/(x - 8) - 960/x = 4.
- Simplify: 960(x - x + 8)/(x(x - 8)) = 4 → 7680/(x(x - 8)) = 4.
- Multiply: 4x(x - 8) = 7680 → x2 - 8x - 1920 = 0.
- Factorize: (x - 48)(x + 40) = 0 → x = 48 or x = -40.
- Discard x = -40 (cost cannot be negative).
- Solution: Cost per book = ₹48.
Alternative Method:
- New number = 960/x + 4, new cost = x - 8.
- Equation: (x - 8)(960/x + 4) = 960.
- Simplify: (x - 8)(960 + 4x)/x = 960.
- Multiply: 960x + 4x2 - 7680 - 32x = 960x.
- Rearrange: 4x2 - 32x - 7680 = 0 → x2 - 8x - 1920 = 0.
- Same solution: x = 48.
Example 4: A picnic’s food budget is ₹480. With 8 fewer students, each pays ₹10 more. Find the number of students who went.
- Let original number of students = x, cost per student = 480/x.
- New number = x - 8, new cost = 480/(x - 8).
- Equation: 480/(x - 8) - 480/x = 10.
- Simplify: 480(x - x + 8)/(x(x - 8)) = 10 → 3840/(x(x - 8)) = 10.
- Multiply: 10x(x - 8) = 3840 → x2 - 8x - 384 = 0.
- Factorize: (x - 24)(x + 16) = 0 → x = 24 or x = -16.
- Discard x = -16 (number cannot be negative).
- Solution: x = 24, students who went = x - 8 = 16.
Alternative Method:
- Let students who went = x, cost = 480/x.
- Original number = x + 8, original cost = 480/(x + 8).
- Equation: 480/x - 480/(x + 8) = 10.
- Simplify: 3840/(x(x + 8)) = 10.
- Multiply: 10x(x + 8) = 3840 → x2 + 8x - 384 = 0.
- Factorize: (x + 24)(x - 16) = 0 → x = -24 or x = 16.
- Discard x = -24.
- Solution: x = 16 students.
FAQs on Solving (Simple) Problems Chapter Notes - Class 10
| 1. What are some common types of problems based on numbers that students encounter in Class 10? |  |
| 2. How can students effectively solve problems based on time and work? |  |
| 3. What strategies can be used to tackle problems based on geometrical figures? |  |
| 4. How do you calculate distance, speed, and time in related problems? |  |
| 5. What is the significance of understanding concepts of Cost Price (C.P.) and Selling Price (S.P.) in mathematics? |  |














