Some Applications of Trigonometry Chapter Notes - Mathematics (Maths) Class 10

Trigonometry, the branch of mathematics dealing with the relationships between the angles and sides of triangles, has several practical applications in various fields.
This chapter discusses the practical applications of trigonometry in everyday life. In trigonometry, we  measure sides of triangle, when particular angle is given.

Height and Distances

Most the buildings, walls, towers we see around are perpendicular to ground. This chapter deals with measurement of heights and distance from certain points with the help of trigonometry if particular angles are known.

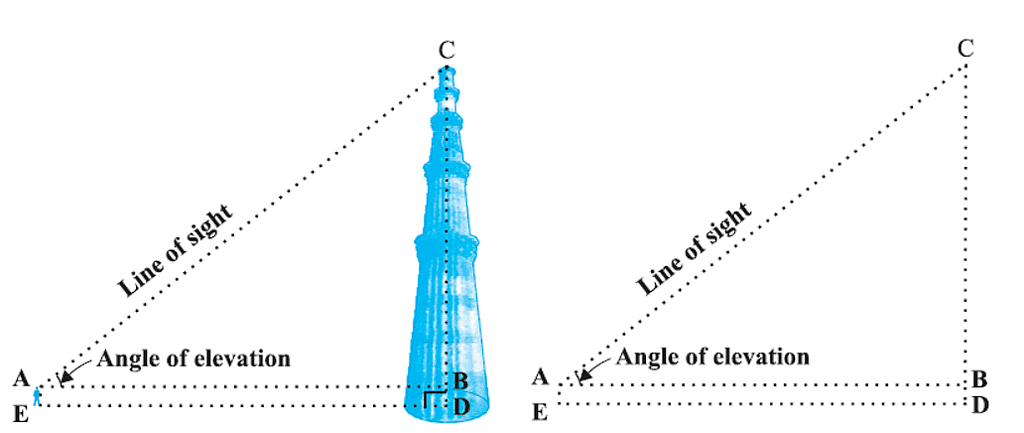
• In the diagram, the line AC from the student's eye to the top of a minar is the line of sight. The angle BAC between the line of sight and the horizontal is the angle of elevation.
• The line of sight is drawn from an observer's eye to the object they're looking at.
  
• Angle of elevation is the angle between the line of sight and the horizontal when viewing an object above eye level.

The line of sight here is below the horizontal, forming the angle of depression. Angle of depression is the angle between the line of sight and the horizontal when viewing an object below eye level.

Line of Sight

When an observer looks from a point O at an object A, then OA is called line of sight.

Angle of Elevation

Suppose that from a point O, you look up at point A, then the angle, the which the line of sight makes with the horizontal line through O is called the angle of elevation of A, as we seen from O.

Here OX is horizontal line. is here angle of elevation.

Angle of Depression

Suppose that from the point O, you look down at an object B, placed below the level of your eye. Then the angle which the line of sight makes with the horizontal line through O is called angle of depression of B for O.

Here, OX is horizontal line. β is here angle of deviation.

An Example of Angle of Elevation and Depression

A man standing on a building will look at a building higher than his. If he sees at the top, he will look at the top he will form angle of elevation. If he look at the bottom he will form angle of depression with bottom of the building.

Solved Examples

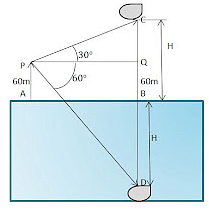
Q1: The angle of elevation of a cloud 60m above a lake is 30° and the angle of reflection of the cloud in the lake is 60°. Find height of the cloud.

Sol: The situation is depicted by the following diagram.

Let AB be the surface of the lake and let P be the point vertically above A such that AP=60m

Let C be the position of cloud and let D be its reflection in the lake.

Let the height of Cloud be H meters.

Then BC=BD=H (Let)

Draw PQ Perpendicular to CD

⇒ ∠QPC=30°, ∠QPD=60°

BQ=AP=60m

CQ=(H-60)m, DQ=(H+60)m

From right triangle ∆ CQP, we have
Let AB be the surface of the lake and let P be the point vertically above A such that AP=60m
Let C be the position of cloud and let D be its reflection in the lake.
Let the height of Cloud be H meters.

Then BC=BD=H (Let)
Draw PQ Perpendicular to CD
⇒∠QPC=30°,∠QPD=60°
BQ=AP=60m
CQ=(H-60)m, DQ=(H+60)m

From right triangle ∆ CQP, we have
PQ/CQ=cot⁡30°
PQ/(H-60) = √3
PQ⇒(H-60) √3 m (i)

From the right triangle ∆ DQP
PQ/DQ=cot⁡60°
⇒PQ=(H+60)/√3 (ii)

From (i) and (ii), we get
(H-60) √3=(H+60)/√3
⇒3H-180=H+60
⇒H=240
So, height of the cloud is H=240m.

Ladder Problem

The angle of elevation of a ladder leaning against a wall is 45° and foot of the ladder is 10m away from the wall. Find the length of ladder. The following diagram depicts the situation

Let OY is the ladder. Let OY=l. YX is the wall on which ladder is leaning on. It is given, ladder is leaned at 45°. Also, distance from the wall to foot of ladder is 10m, OX=d=10m. It is given √2=1.414
From the diagram,
cos 45°= OX/OY = d/l
⇒ l=d/cos 45°
We know that cos 45° = 1/√2
So, l = d/(1/√2) = √2 d
l = √2×10 m = 10√2 m = 10×1.414 = 14.14m
So, length of ladder is 14.14m