Tangents and Intersecting Chords Chapter Notes | Mathematics Class 10 ICSE PDF Download
Introduction
- Imagine a circle and a straight line dancing together on a plane!
- They can interact in three exciting ways:

- The line might shy away, not touching the circle at all (no contact).
- The line could boldly cut through the circle, meeting it at two points, known as a secant.
- The line might gently kiss the circle at just one point, called a tangent, creating a special point of contact.
- A secant is a line that intersects a circle at two points, like a sword slicing through.
- A tangent touches the circle at exactly one point, like a fleeting touch.
- The point where the tangent meets the circle is called the point of contact.
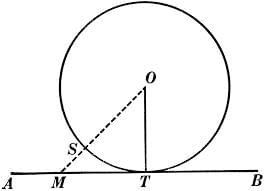
Theorem 10: Tangent and Radius are Perpendicular
 Tangent-Radius Perpendicular
Tangent-Radius PerpendicularThe tangent at any point on a circle is perpendicular to the radius passing through that point.
Stepwise Explanation:
- Consider a circle with center O. A tangent AB touches the circle at point P, and OP is the radius.
- Take another point Q on the tangent AB (not P) and draw line OQ.
- Since Q lies outside the circle, OP is shorter than OQ (the shortest distance from a point to a line is the perpendicular).
- Among all lines from O to AB, OP is the shortest, so OP is perpendicular to AB.
Key Points to Remember:
- No tangent can pass through a point inside the circle.
- Exactly one tangent can be drawn at a point on the circle’s circumference.
- Two tangents can be drawn from a point outside the circle.
Corollary: Properties of Two Tangents from an Exterior Point
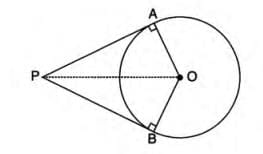
When two tangents are drawn from an exterior point to a circle, they have special properties.
Properties:
- The lengths of the two tangents are equal (PA = PB).
- The angles subtended by the tangents at the center are equal (∠AOP = ∠BOP).
- The tangents are equally inclined to the line joining the exterior point to the center (∠APO = ∠BPO).
- Consider a circle with center O. From an exterior point P, draw tangents PA and PB.
- In triangles AOP and BOP:
- OA = OB (radii of the same circle).
- ∠OAP = ∠OBP = 90° (radius is perpendicular to tangent).
- OP = OP (common side).
- Triangles AOP and BOP are congruent by RHS (Right angle-Hypotenuse-Side).
- Thus, PA = PB, ∠AOP = ∠BOP, and ∠APO = ∠BPO (corresponding parts of congruent triangles).
Theorem 11: Point of Contact Lies on Line Through Centers
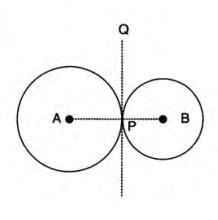
Case I: External Touching
- When two circles touch externally, their point of contact lies on the line joining their centers.
- Consider two circles with centers A and B, touching externally at point P.
- Draw a common tangent PQ through P and join AP and BP.
- ∠APQ = 90° and ∠BPQ = 90° (radius is perpendicular to tangent).
- ∠APQ + ∠BPQ = 180°, so ∠APB = 180°, meaning APB is a straight line.
- Thus, P lies on line AB.
Case II: Internal Touching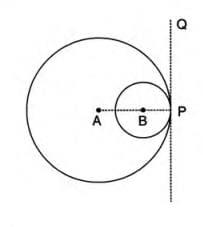
- When two circles touch internally, the point of contact lies on the line joining the centers, extended if necessary.
- Consider two circles with centers A and B, touching internally at point P.
- Since AP and BP are both perpendicular to PQ at P, they lie on the same line.
- Thus, P lies on the extended line AB.
Formulas for Distance Between Centers
For two circles with radii r1 and r2, and distance d between their centers:
- External touching: d = r1 + r2
- Internal touching: d = r1 - r2 (if r1 > r2) or d = r2 - r1 (if r2 > r1)
Additional Notes:
- If tangents AB and CD to a circle at points P and Q are parallel, then PQ is the diameter of the circle.
- Concentric circles share the same center.
Theorem 12: Product of Chord Segments
Case I: Internal Intersection
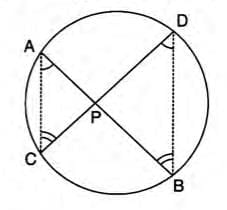
- When two chords intersect inside a circle, the product of the lengths of their segments is equal.
- Formula: PA × PB = PC × PD
- Consider chords AB and CD intersecting at point P inside the circle.
- Join AC and BD to form triangles APC and BPD.
- ∠A = ∠D and ∠C = ∠B (angles in the same segment).
- Triangles APC and BPD are similar by AA similarity.
- Thus, PA/PD = PC/PB, so PA × PB = PC × PD.
Case II: External Intersection
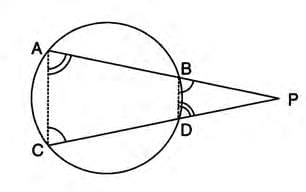
- When two chords, extended, intersect outside a circle, the product of the lengths of their segments is equal.
- Consider chords AB and CD, extended to intersect at point P outside the circle.
- Join AC and BD to form triangles PAC and PDB.
- ∠A = ∠PDB and ∠C = ∠PBD (exterior angle of a cyclic quadrilateral equals the interior opposite angle).
- Triangles PAC and PDB are similar by AA similarity.
Theorem 13: Angle Between Tangent and Chord

- The angle between a tangent and a chord at the point of contact equals the angle in the alternate segment.
- Formula: ∠BAQ = ∠ACB and ∠BAP = ∠ADB
- Stepwise Explanation:
- Consider a circle with center O. Tangent PQ touches at A, and chord AB is drawn.
- Draw diameter AOR and join RB.
- In triangle ABR, ∠ABR = 90° (angle in a semicircle).
- Thus, ∠ARB + ∠RAB = 90°.
- Since ∠OAQ = 90° (radius perpendicular to tangent), ∠RAB + ∠BAQ = 90°.
- Therefore, ∠ARB = ∠BAQ.
- But ∠ARB = ∠ACB (angles in the same segment), so ∠BAQ = ∠ACB.
- Since ∠BAP + ∠BAQ = 180° (straight line) and ∠ACB + ∠ADB = 180° (opposite angles of a cyclic quadrilateral), ∠BAP = ∠ADB.
Theorem 14: Tangent and Chord Intersection Externally
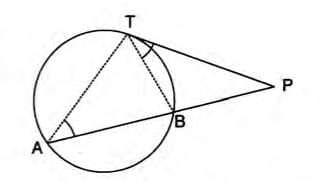
- When a chord and a tangent intersect externally, the product of the chord’s segment lengths equals the square of the tangent’s length from the point of contact to the intersection.
- Formula: PA × PB = PT2
- Stepwise Explanation:
- Consider chord AB and tangent TP intersecting at P outside the circle.
- Join TA and TB to form triangles PAT and PTB.
- ∠PTB = ∠A (angle in the alternate segment).
- ∠P = ∠P (common angle).
- Triangles PAT and PTB are similar by AA similarity.
- Thus, PA/PT = PT/PB, so PA × PB = PT2.
Solved Examples
Example 1: Radius of Inscribed Circle In triangle PQR, PQ = 24 cm, QR = 7 cm, and ∠PQR = 90°. Find the radius of the inscribed circle.
Solution: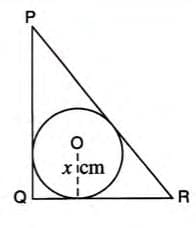
- Since ∠PQR = 90°, use Pythagoras: PR2 = PQ2 + QR2 = 242 + 72 = 576 + 49 = 625, so PR = 25 cm.
- Let the incircle touch PQ at A, QR at B, and PR at C, with radius x cm.
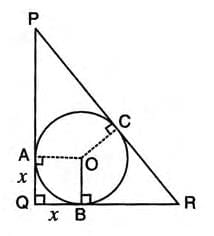
- OAQB is a square, so AQ = BQ = x cm.
- PA = PQ - AQ = (24 - x) cm, RB = QR - BQ = (7 - x) cm.
- Tangents from an exterior point are equal: PC = PA = (24 - x) cm, RC = RB = (7 - x) cm.
- PR = PC + RC: 25 = (24 - x) + (7 - x) = 31 - 2x.
- Solve: 2x = 31 - 25 = 6, so x = 3.
- Radius of the inscribed circle = 3 cm.
Example 2: Equation for Radius of Third Circle Centers P and Q of circles with radii 9 cm and 2 cm are 17 cm apart. A third circle with center R and radius x cm touches both externally, with ∠PRQ = 90°. Find x.
Solution: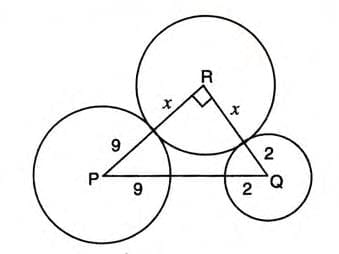
- For external touching, PR = 9 + x, QR = 2 + x, PQ = 17 cm.
- Since ∠PRQ = 90°, apply Pythagoras in triangle PRQ: PR2 + QR2 = PQ2.
- (9 + x)2 + (2 + x)2 = 172.
- Expand: 81 + 18x + x2 + 4 + 4x + x2 = 289.
- Simplify: 2x2 + 22x + 85 = 289, so 2x2 + 22x - 204 = 0.
- Divide by 2: x2 + 11x - 102 = 0.
- Factorize: (x + 17)(x - 6) = 0, so x = -17 or x = 6.
- Since radius cannot be negative, x = 6 cm.
Example 3: Length of Direct Common Tangent Two circles with radii 25 cm and 9 cm touch externally. Find the length of the direct common tangent.
Solution: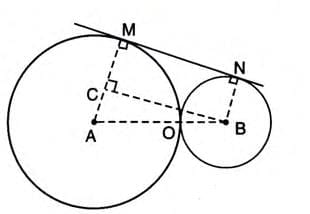
- Centers A and B, touching externally at O. MN is the direct common tangent.
- Draw BC ⊥ AM. BCMN is a rectangle, so BC = MN.
- AB = OA + OB = 25 + 9 = 34 cm.
- AC = AM - BN = 25 - 9 = 16 cm.
- In right triangle ABC, AB2 = AC2 + BC2.
- 342 = 162 + BC2, so 1156 = 256 + BC2, BC2 = 900, BC = 30 cm.
- Length of direct common tangent MN = BC = 30 cm.
Example 4: Length of Transverse Common Tangent Centers of two circles with radii 6 cm and 2 cm are 10 cm apart. Find the length of the transverse common tangent.
Solution:
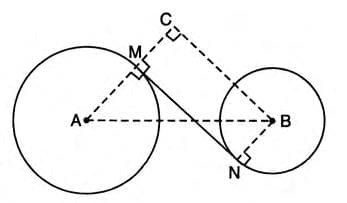
- Centers A and B, MN is the transverse common tangent.
- AB = 10 cm, AM = 6 cm, BN = 2 cm.
- Draw BC ⊥ AM extended. BCMN is a rectangle, so MN = BC, CM = BN = 2 cm.
- AC = AM + CM = 6 + 2 = 8 cm.
- In right triangle ABC, AB2 = BC2 + AC2.
- 102 = BC2 + 82, so 100 = BC2 + 64, BC2 = 36, BC = 6 cm.
- Length of transverse common tangent MN = BC = 6 cm.
Example 5: Angles in Triangle with Tangents In triangle PQR, PQ = QR, ∠RQP = 68°, PC and QC are tangents to a circle with center O. Find ∠QOP and ∠QCP.
Solution:
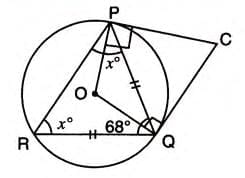
- Since PQ = QR, triangle PQR is isosceles, so ∠QPR = ∠QRP.
- In triangle PQR, ∠QPR + ∠QRP + ∠RQP = 180°.
- Let ∠QPR = ∠QRP = x. Then x + x + 68° = 180°, so 2x = 112°, x = 56°.
- ∠QRP = 56°.
- Angle at center is twice the angle at circumference: ∠QOP = 2 × ∠QRP = 2 × 56° = 112°.
- In quadrilateral POQC, ∠QOP = 112°, ∠OPC = 90°, ∠OQC = 90° (radius ⊥ tangent).
- Sum of angles: ∠QOP + ∠OPC + ∠OQC + ∠QCP = 360°.
- 112° + 90° + 90° + ∠QCP = 360°, so ∠QCP = 68°.
|
74 videos|198 docs|30 tests
|
FAQs on Tangents and Intersecting Chords Chapter Notes - Mathematics Class 10 ICSE
| 1. What is the significance of Theorem 10 regarding tangents and radii in circles? |  |
| 2. How do the properties of two tangents from an exterior point assist in solving problems? |  |
| 3. What does Theorem 12 about the product of chord segments state, and how is it applied? |  |
| 4. Can you explain the Angle Between Tangent and Chord in simple terms? |  |
| 5. What is the importance of understanding the tangent and chord intersection externally as per Theorem 14? |  |
















