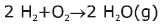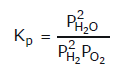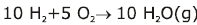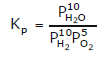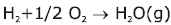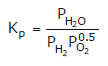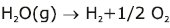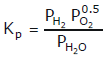Law of Chemical Equilibrium & Equilibrium Constant | Chemistry Class 11 - NEET PDF Download
| Table of contents |

|
| Dynamic Equilibrium: Static and Dynamic Equilibrium |

|
| Chemical Equilibrium |

|
| Equilibrium Constant |

|
| Significance of Equilibrium Constant |

|
| Solved Examples |

|
Dynamic Equilibrium: Static and Dynamic Equilibrium
When the two opposing forces are operating simultaneously and independent of each other, two states (state 1 and state 2) are formed with the interchange between the two states. The states are said to be in dynamic equilibrium. A double-sided arrow represents the dynamic equilibrium ”A ⇌ B”.
Depending on the composition of the two states, two equilibriums, namely physical or chemical equilibrium are defined.
What is Dynamic Equilibrium?
Dynamic Equilibrium can be defined as the state of a given system in which the reversible reaction taking place in it stops changing the ratio of reactants and products, but there is a movement of substances between the reactants and the products. This movement occurs at an equal rate and there is no net change of the reactant and product ratio.
For these types of equilibria, the equilibrium constants are represented with the help of the rate constants for the forward and backward reactions. Systems maintaining a dynamic equilibrium are examples of systems in steady states.
Difference Between Static and Dynamic Equilibrium
Static equilibrium refers to a condition where the reaction occurring in a system is completely halted and there exists no movement between the reactants and the products corresponding to the chemical reaction.
If the forces acting on an object cancel each other, in addition to the constancy of content and composition, no movement of the object takes place. This is static equilibrium.
The key differences between static and dynamic equilibrium are tabulated below: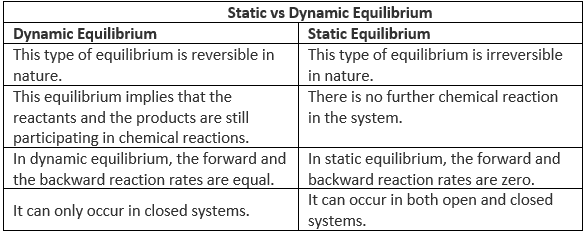
However, the resultant force acting on both of these types of equilibria in a system is zero. Generally, neither of these types of equilibrium display visible changes.
Examples of Dynamic Equilibrium
A few important examples of dynamic equilibrium in our everyday life are listed below:
- A new bottle of an aerated drink has a specific value for the concentration of the carbon dioxide present in the liquid phase in it. When the bottle is opened and half of the drink is poured out of it, the liquid carbon dioxide is slowly converted into gaseous carbon dioxide until a new point of equilibrium is reached, and the rate of conversion of CO2 from gas to liquid is equal to the rate of conversion of CO2 from liquid to the gaseous phase.
- The single-phase system in which acetic acid undergoes dissociation, leading to an acid-base equilibrium. This state of dynamic equilibrium can be described by the following reaction.
Reaction: CH3COOH ⇌ CH3COO– + H+ - In the gaseous phase can be observed in the dimerization of nitrogen dioxide.
Reaction: 2NO2 ⇌ N2O4 - Henry’s Law is applicable in the first example of dynamic equilibrium provided above, wherein the equilibrium concentration of carbon dioxide in the liquid phase is proportional to the partial pressure of the CO2 gas in the bottle.
- Industrial synthesis of ammonia via Haber’s process.
Reaction: N2 (g) + 3H2 (g) ⇌ 2NH3 (g).
Chemical Equilibrium
- If a reversible reaction is carried out in a closed vessel, a stage is attained where the speed of the forward reaction equals the speed of the backward reaction. It corresponds to chemical equilibrium.
- At equilibrium, Rate of forward reaction = Rate of backward reaction.
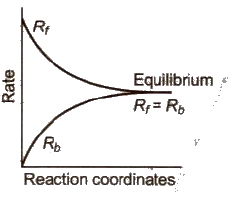
Characteristics of Chemical Equilibrium:
- Equilibrium can be attained from either side.
- Equilibrium is dynamic in nature, i.e., at equilibrium reaction does not stop.
- At equilibrium, there is no change in the concentration of various species.
- The equilibrium state remains unaffected by the presence of a catalyst. Catalyst helps to attain the equilibrium state rapidly.
- The observable physical properties of the process become constant.
➢ Law of Mass Action
- Guldberg and Waage states that the rate of a chemical reaction is directly proportional to the product of the active masses of the reacting substances.
- For a general reaction,
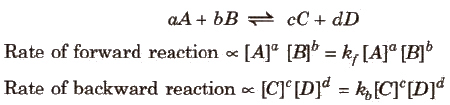
where kf and kb are rate constants. - Δng = no. of moles of gaseous products - no. of moles of gaseous reactants
i.e. Δng = ((c + d) - (a + b)) - In heterogeneous equilibrium, the active mass of pure solids and liquids are taken as unity.
➢ Law of Chemical Equilibrium
- At a given temperature, the product of concentrations of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the product of concentrations of the reactants raised to their individual stoichiometric coefficients has a constant value. This is known as the equilibrium Law or Law of Chemical Equilibrium.
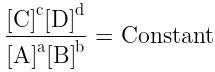
Equilibrium Constant
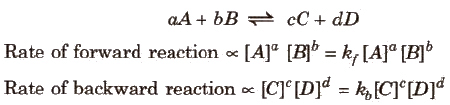
- At equilibrium, Rate of forward reaction = Rate of backward reaction
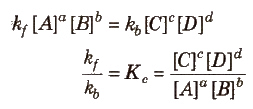
- Kc is known as the equilibrium constant.
- Unit of Kc = (mol L-1)Δng
➢ Use of Partial Pressures Instead of Concentration
- For gaseous reactions, partial pressures are conveniently used since at any fixed temperature partial pressure is directly proportional to concentration.
- For a general gaseous reaction,
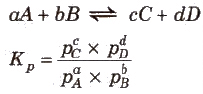
- Unit of Kp = (atm)Δng
- Example:
For the reaction, N2(g) + 3 H2(g) ⇋ 2NH3(g)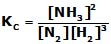 ,
, 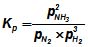
➢ Units of Equilibrium Constant
- The value of equilibrium constant Kc can be calculated by substituting the concentration terms in mol/L and for Kp partial pressure is substituted in Pa, kPa, bar, or atm.
- This results in units of equilibrium constant based on molarity or pressure unless the exponents of both the numerator and denominator are the same.
- For the reactions,
H2(g) + I2(g)2HI, Kc and Kp have no unit.
N2O4(g)2NO2 (g), Kc has unit mol/L and Kp has a unit bar or atm
- Equilibrium constants can also be expressed as dimensionless quantities if the standard state of reactants and products are specified.
- For a pure gas, the standard state is 1 bar. Therefore a pressure of 4 bar in the standard state can be expressed as 4 bar/1 bar = 4, which is a dimensionless number.
- The standard state (C0) for a solute is 1 molar solution and all concentrations can be measured with respect to it. The numerical value of the equilibrium constant depends on the standard state chosen.
- Thus in this system, both Kp and Kc are dimensionless quantities and represented as Kp° & KC° respectively
➢ Relation between Kc and Kp
For the reaction, aA + bB ⇌ cC + dD
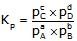
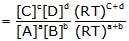
Kp=Kc(RT)Δng
where Δng= (c +d) - (a +b)Relation between Kc and Kp for different types of reactions:
(i) When Δng = 0, Kp = Kc
(ii) When Δng = +ve, Kp > Kc
(iii) When Δng = -ve, Kp < Kc
➢ Characteristics of Equilibrium Constant, Kp or Kc
- It has a definite value for every chemical reaction at a particular temperature.
- The more is the value of Kc or Kp, the more is the extent of completion of reaction, i.e., Kc < 1 indicates a lesser concentration of products than reactants.K ≥ 103 shows completion of the reaction and K ≤ 10-3 shows that the reaction does not proceed at all.
- When the reaction can be expressed as a sum of two other reactions, the Kc of the overall reaction is equal to the product of equilibrium constants of individual reactions.
Reaction 1 with equilibrium constant K1: A + B ⇌ C + D
Reaction 2 with equilibrium constant K2: E + F ⇌ G
Reaction 3 with equilibrium constant K3: A + B + E + F ⇌ C + D + G
⇒→ K3 = K1 × K2
- The equilibrium constant is independent of the initial concentrations of reactants.
- The equilibrium constant is independent of the presence of the catalyst.
- Kc for the backward reaction is the inverse of Kc for the forward reaction.
For forward reaction,
For backward reaction, - If an equation is multiplied by n, the K becomes Kn, and if it is divided by m, the K becomes m√K.
Reaction with equilibrium constant K1: A + B ⇌ C + D
After multiplying by n,
New reaction with equilibrium constant K2: nA + nB ⇌ nC + nD - In equilibrium constant expression if activities are used in places of the molar concentration, h becomes dimensionless.
Significance of Equilibrium Constant
1. Using Keq to Predict Relative Concentrations
- The size of the equilibrium constant can give us information about the relative amounts of reactants and products present at equilibrium.
(a) When K << 1: The reaction lies to the left (mostly reactants)
(b) When K >> 1: The reaction lies to the right (mostly products)
(c) When K = 1: The reaction lies in the middle (mix of reactants and products)
2. Calculating Equilibrium concentrations
Example: Phosgene is a poisonous gas that dissociates at a high temperature into two other poisonous gases, carbon monoxide and chlorine. The equilibrium constant Kp= 0.0041 atm at 600K.
Find the equilibrium composition of the system after 0.124 atm of COCl2 initially is allowed to reach equilibrium at this temperature.
Sol. 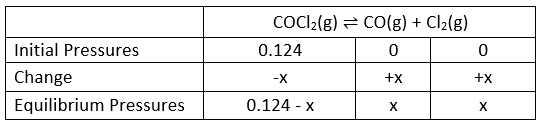
Substitution of the equilibrium pressures into the equilibrium expression gives:
This expression can be rearranged into standard polynomial form:
x2 + 0.0041x - 0.00054 = 0
Solved by the quadratic formula, but we will simply obtain an approximate solution by iteration.
Because the equilibrium constant is small, we know that x will be rather small compared to 0.124, so the above relation can be approximated by
which gives x=0.025.
To see how good this is, substitute this value of x into the denominator of the original equation and solve again:
This time, solving for x gives 0.0204.
Iterating once more, we get
and x = 0.0206, which is sufficiently close to the previous to be considered the final result. The final partial pressures are then 0.104 atm for COCl2, and 0.0206 atm each for CO and Cl2.
Note: Using the quadratic formula to find the exact solution yields the two roots -0.0247 (which we ignore) and 0.0206, which show that our approximation is quite good.
3. Reaction Quotient (Q)
- At each point in a reaction, we can write a ratio of concentration terms having the same forms as the equilibrium constant expression. The ratio is called the reaction quotient denoted by symbol Q.
- Q=
- It helps in predicting the direction of a reaction:
(i) If Q > KC reaction will proceed in a backward direction until equilibrium is reached.
(ii) If Q < KC reaction will proceed in forward direction until equilibrium is established.
(iii) If Q = KC reaction is at equilibrium.
Example. For the reaction NOBr (g)
NO(g) + 1/2 Br2(g) , Kp=0.15 atm at 90°C. If NOBr, NO, and Br2 are mixed at this temperature having partial pressures 0.5 atm,0.4 atm & 2.0 respectively, will Br2 be consumed or formed?
Sol.
, Kp=0.15
Hence, the reaction will shift in the backward direction, Therefor Br2 will be consumed.
4. Degree of Dissociation & Vapour Density
Ex. The Vapour Density of mixture of PCl5, PCl3 and Cl2 is 92. Find the degree of dissociation of PCl5.
Sol.
1 0 0
1 - x x x
= 104.25 ,
, α =0.13
Solved Examples
Q.1. Given the following equilibrium constants:
(1) CaCO3(s) → Ca2+ (aq) + CO32-(aq); K1=10-8.4
(2) HCO3-(aq) → H+ (aq) + CO32-(aq); K2=10-10.3
Calculate the value of K for the reaction CaCO3(s) + H (aq) → Ca2 (aq) + HCO3-(aq)
Sol.
The net reaction is the sum of reaction 1 and the reverse of reaction 2:
Reaction 1: CaCO3(s) → Ca2 (aq) +CO32-(aq); K1=10-8.4
Reaction 2: H+ (aq) + CO32-(aq)→ HCO3-(aq); K-2=10-(-10.3)
Net Reaction: CaCO3(s) + H+ (aq) → Ca2 (aq) + HCO3-(aq);
K=K1/K2=10(-8.4 +10.3) =10+1.9
Comment: This net reaction describes the dissolution of limestone by acid; it is responsible for the eroding effect of acid rain on buildings and statues. This is an example of a reaction that has practically no tendency to take place by itself (the dissolution of calcium carbonate) begin "driven" by a second reaction having a large equilibrium constant.
From the standpoint of the LeChâtelier principle, the first reaction is "pulled to the right" by the removal of carbonate by the hydrogen ion. "Coupled" reactions of this type are widely encountered in all areas of chemistry, and especially in biochemistry, in which a dozen or so reactions may be linked in this way.
Q.2. The synthesis of HBr from hydrogen and liquid bromine has an equilibrium constant Kp = 4.5×1015 at 25°C. Given that the vapor pressure of liquid bromine is 0.28 atm, find Kp for the homogeneous gas-phase reaction at the same temperature.
Sol: The net reaction we seek is the sum of the heterogeneous synthesis and the reverse of the vaporization of liquid bromine:
 View Answer
View Answer 
Note:
Some of the possibilities for the reaction involving the equilibrium between gaseous water and its elements:
|
114 videos|263 docs|74 tests
|
FAQs on Law of Chemical Equilibrium & Equilibrium Constant - Chemistry Class 11 - NEET
| 1. What is the difference between static and dynamic equilibrium? |  |
| 2. What is the significance of the equilibrium constant? |  |
| 3. How is the equilibrium constant calculated? |  |
| 4. Can the equilibrium constant change with temperature? |  |
| 5. How can the equilibrium constant be used to determine the position of equilibrium? |  |