Dynamics of Circular Motion - Notes | Study Physics Class 11 - NEET

Dynamics of Circular Motion
We know that linear acceleration of a particle in circular motion has two components, tangential and radial (or centripetal). So, normally we resolve the forces acting on the particle in two directions:

(i) Tangential

(ii) Radial

In tangential direction, net force on the particle is ma_t and in radial direction net force is ma_r. In uniform circular motion, tangential acceleration is zero. Hence, net force in tangential direction is zero and in radial direction

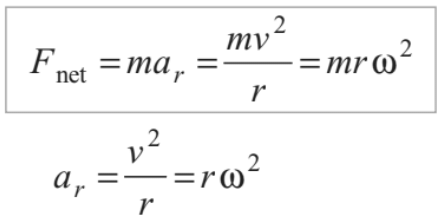
This net force (towards centre) is also called centripetal force.

In most of the cases plane of our uniform circular motion will be horizontal and one of the tangent is in vertical direction also. So, in this case we resolve the forces in:

(i) horizontal radial direction

(ii) vertical tangential direction

In vertical tangential direction net force is zero (a_t =0) and in horizontal radial direction (towards centre) net force is mv²/r or mrω²

Note:  Centripetal force mv²/r or mrω² (towards centre) does not act on the particle but this much force is required to the particle for rotating in a circle (as it is accelerated due to change in direction of velocity). The real forces acting on the particle provide this centripetal force or we can say that vector sum of all the forces acting on the particle is equal to mv²/r  or mrω² (in case of uniform circular motion). The real forces acting on the particle may be, friction force, weight, normal reaction, tension etc.

Conical Pendulum

If a small particle of mass m tied to a string is whirled in a horizontal circle, as shown in Fig. The arrangement is called the ‘conical pendulum’. In case of conical pendulum, the vertical component of tension balances the weight in tangential direction, while its horizontal component provides the necessary centripetal force in radial direction

(towards centre). Thus,

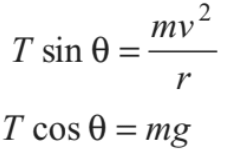
From these two equations, we can find

∴ Angular speed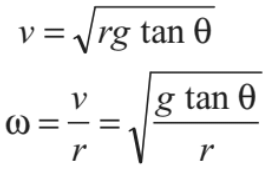  

So, the time period of pendulum is

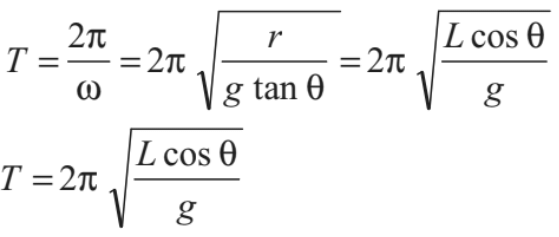         (as r = L sin θ)

Motion of a Particle Inside a Smooth Cone

A particle of mass ‘m’ is rotating inside a smooth cone in horizontal circle of radius ‘r’ as shown in figure. constant speed of the particle is suppose ‘v’. Only two forces are acting on the particle in the shown directions:

(i) Normal reaction N

(ii) Weight mg

We have resolved these two forces in vertical tangential direction and horizontal radial direction. In vertical tangential direction, net force is zero.

∴ N cosθ = mg

In horizontal radial direction (towards centre), net force is mv²/r

∴

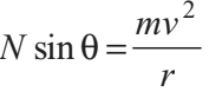
Circular Turning on Roads

When vehicles go through turnings, they travel along a nearly circular arc. There must be some force which will produce the required centripetal acceleration. If the vehicles travel in a horizontal circular path, this resultant force is also horizontal. 

The necessary centripetal force is being provided to the vehicles by following three ways:

1. By Friction only

2. By Banking of Roads only

3. By Friction and Banking of Roads both.

In real life the necessary centripetal force is provided by friction and banking of roads both. Now let us write equations of motion in each of the three cases separately and see what are the constant in each case.

➢ By Friction Only 

Suppose a car of mass m is moving at a speed v in a horizontal circular arc of radius r. In this case, the necessary centripetal force to the car will be provided by force of friction f acting towards centre

Thus, f = mv²/r

Further, limiting value of f is or μN or f_L = μN = μmg (N = mg)

Therefore, for a safe turn without sliding  mv²/r ≤ f_L

or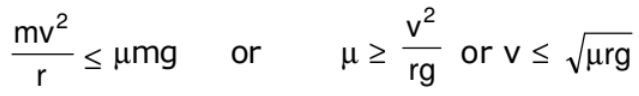

Here, two situations may arise. If m and r are known to us, the speed of the vehicle should not exceed 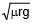 and if v and r are known to us, the coefficient of friction should be greater than .

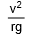➢ By Banking of Roads Only 

Friction is not always reliable at circular turns if high speeds and sharp turns are involved to avoid dependence on friction, the roads are banked at the turn so that the outer part of the road is somewhat lifted compared to the inner part.

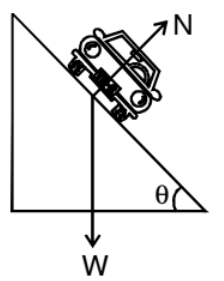
Applying Newton's second law along the radius and the first law in the vertical direction.

from these two equations, we get

➢ By Friction and Banking of Road Both

If a vehicle is moving on a circular road which is rough and banked also, then three forces may act on the vehicle, of these force, the first force, i.e., weight (mg) is fixed both in magnitude and direction.

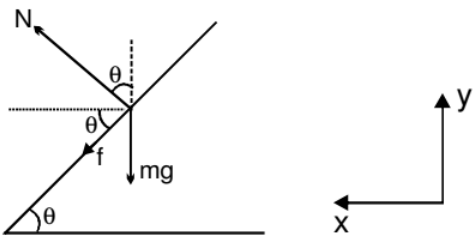
The direction of second force i.e., normal reaction N is also fixed (perpendicular or road) while the direction of the third i.e., friction f can be either inwards or outwards while its magnitude can be varied upto a maximum limit (f_L = mN). So the magnitude of normal reaction N and directions plus magnitude of friction f are so adjusted that the resultant of the three forces mentioned above is mv²/r towards the center. Of these m and r are also constant. Therefore, magnitude of N and directions plus magnitude of friction mainly depends on the speed of the vehicle v. Thus, situation varies from problem to problem. Even though we can see that :

(i) Friction f will be outwards if the vehicle is at rest v = 0. Because in that case the component weight mg sinθ is balanced by f.

(ii) Friction f will be inwards if

v >

(iii) Friction f will be outwards if

v <  and

(iv) Friction f will be zero if

v =

(v) For maximum safe speed 

As maximum value of friction f = μN
∴

∴

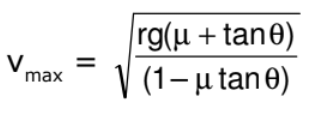
similarly;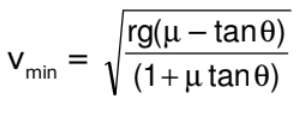

• The expression tanθ = 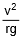 also gives the angle of banking for an aircraft, i.e., the angle through which it should tilt while negotiating a curve, to avoid deviation from the circular path.  
• The expression tanθ =  also gives the angle at which a cyclist should lean inward when rounding a corner. In this case, θ is the angle which the cyclist must make with the vertical to negotiate a safe turn.

Death well

A motor cyclist is driving in a horizontal circle on the inner surface of vertical cyclinder of radius R. Friction coefficient between tyres of motorcyclist and surface of cylinder is m. Find out the minimum velocity for which the motorcyclist can do this. v is the speed of motor cyclist and m is his mass.

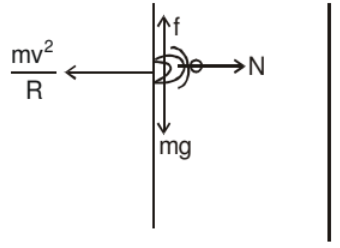
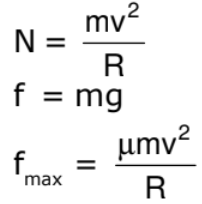
Cyclist does not drop down when

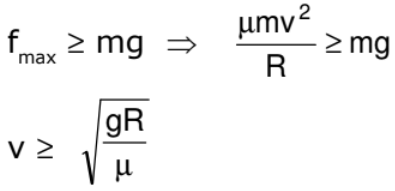
Motion of a Cyclist on a Circular Path

Suppose a cyclist is going at a speed v on a circular horizontal road of radius r which is not banked. Consider the cycle and the rider together as the system. The centre of mass C (figure shown) of the system is going in a circle with the centre at O and radius r.

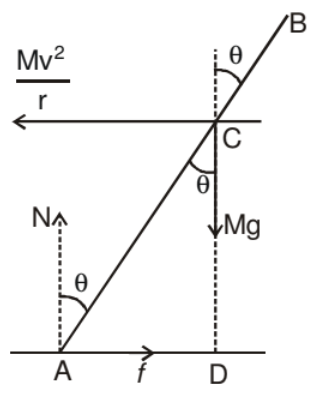
Let us choose O as the origin, OC as the X-axis and vertically upward as the Z-axis. This frame is rotating at an angular speed w = v/r about the Z-axis. In this frame the system is at rest. Since we are working from a rotating frame of reference, we will have to apply a centrifugal force on each particle. The net centrifugal force on particle will be Mω²r = Mv²/r, where M is the total mass of the system. This force will act through the centre of mass. Since the system is at rest in this frame, no other pseudo force is needed.

Figure in shows the forces. The cycle is bent at an angle θ with the vertical. The forces are

(i) weight Mg,

(ii) normal force N

(iii) friction f

(iv) Centrifugal force 

In the frame considered, the system is at rest. Thus, the total external force and the total external torque must be zero. Let us consider the torques of all the forces about the point A. The torques of N and f about A are zero because these forces pass through A. The torque of Mg about A is Mg(AD) in the clockwise direction and that of Mv²/r is Mv²/r (CD) in the anticlockwise direction. For rotational equilibrium,

Mg(AD) = Mv²/r (CD)

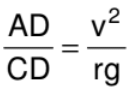
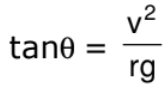
Thus, the cyclist bends at an angle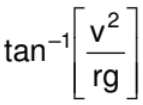with the vertical.

Centrifugal Force

When a body is rotating in a circular path and the centripetal force vanishes, the body would leave the circular path. To an observer A who is not sharing the motion along the circular path, the body appears to fly off tangentially at the point of release. To another observer B, who is sharing the motion along the circular path (i.e., the observer B is also rotating with the body which is released, it appears to B, as if it has been thrown off along the radius away from the centre by some force. This inertial force is called centrifugal force.)

Its magnitude is equal to that of the centripetal force = mv²/r . Centrifugal force is a fictitious force which has to be applied as a concept only in a rotating frame of reference to apply Newton's law of motion in that frame)

FBD of ball w.r.t non-inertial frame rotating with the ball.

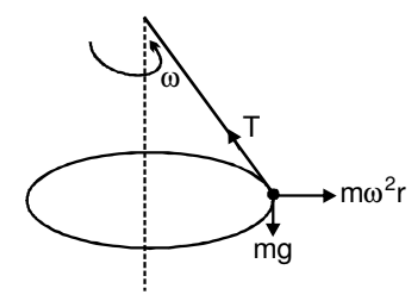
Suppose we are working from a frame of reference that is rotating at a constant, angular velocity ω with respect to an inertial frame. If we analyse the dynamics of a particle of mass m kept at a distance r from the axis of rotation, we have to assume that a force mrω² act radially outward on the particle. Only then we can apply Newton's laws of motion in the rotating frame. This radially outward pseudo force is called the centrifugal force.

Simple Pendulum 

A simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical.

The force acting on the bob are (figure)

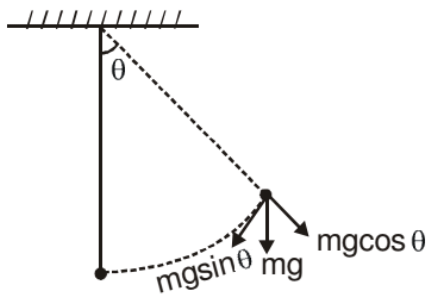
(i) Tension T

(ii) Weight mg

As the bob moves in a vertical circle with centre at O, the radial acceleration is v²/L towards O. Taking the components along this radius and applying Newton's second law, we get

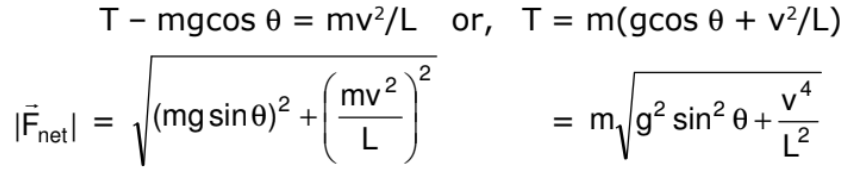
Circular Motion in Horizontal Plane 

A ball of mass m attached to a light and inextensible string rotates in a horizontal circle of radius r with an angular speed w about the vertical. If we draw the force diagram of the ball. 

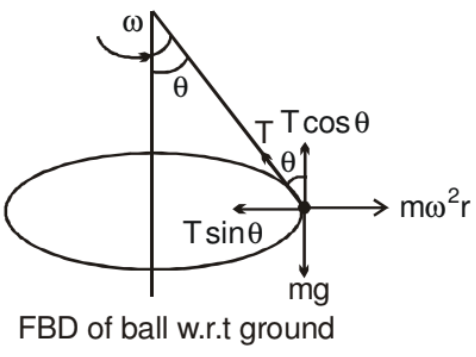
We can easily see that the component of tension force along the centre gives the centripetal force and component of tension along vertical balances the gravitation force. Such a system is called a conical pendulum.

Motion in a Vertical Circle
Suppose a particle of mass m is attached to an inextensible light string of length R. The particle is moving in a vertical circle of radius R about a fixed point O. It is imparted a velocity u in horizontal direction at lowest point A. Let v be its velocity at point B of the circle as shown. 

h = R(1 - cosθ)   ......(i)         

From conservation of mechanical energy

1/2 m(u²- v²) = mgh

or v² = u² - 2gh   .....(ii)

The necessary centripetal force is provided by the resultant of tension T and mg cosθ

......(iii)

Now, following three conditions arise depending on the value of u.

➢ Condition of Looping the Loop (u ≥ √5gR)

The particle will complete the circle if the string does not slack even at the highest point (θ = π). Thus, tension in the string should be greater than or equal to zero (T ≥ 0) at θ = π.  In critical case substituting T = 0 and θ = π in above equation, we get

 (at highest point)

Substituting θ = π in Eq.(i), h=2R

Therefore, we have

Thus, if u ≥ √5gR , the particle will complete the circle. At u = √5gR, velocity at highest point is v = √gR and tension in the string is zero.

Substituting θ = 0° and  u = √5gR in Eq. (iii), we get T = 6mg or in the critical condition tension in the string at lowest position is 6mg. This is shown in Figure.

If  u < √5gR , following two cases are possible.

➢ Condition of Leaving the Circle (√2gR < u < √5gR)

If u < √5gR the tension in the string will become zero before reaching the highest point. From Eq. (iii), tension in the string becomes zero (T=0)

where,

Substituting this value of cos θ in Eq. (i), we get

.......(iv)

or we can say that at height h₁ tension in the string becomes zero. Further, if u < √5gR , velocity of the particle becomes zero when

.......(v)

i.e. at height h₂ velocity of particle becomes zero.

Now, the particle will leave the circle if tension in the string becomes zero but velocity is not zero or T = 0 but v ≠ 0. This is possible only when

Therefore, if √2gR < u < √5gR the particle leaves the circle.

From Eq. (iv), we can see that h R > if u² > 2gR . Thus, the particle will leave the circle when h >R  or 90 < θ <180 ° . This situation is shown in the Fig.

Note: After leaving the circle, the particle will follow a parabolic path as the particle

comes under gravity.

➢ Condition of Oscillation (0 < u < √2gR)

The particle will oscillate, if velocity of the particle becomes zero but tension in the string is not zero. or v = 0, but T ≠ 0. This is possible when

Moreover, if h₁=h_2, u = √2gR and tension and velocity both becomes zero simultaneously.

Further, from Eq. (iv), we can see that h ≤ R  if u ≤ √2gR Thus, for 0< u ≤ √2gR 

particle oscillates in lower half of the circle (0°<θ ≤ 90°).

This situation is shown in the figure.

Note: The above three conditions have been derived for a particle moving in a vertical circle attached to a string.The same conditions apply, if a particle moves inside a smooth spherical shell of radius R. The only difference is that the tension is replaced by the normal reaction N.