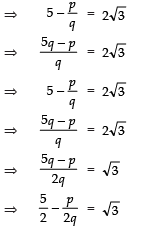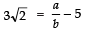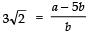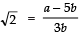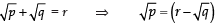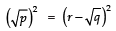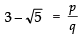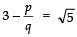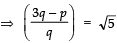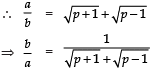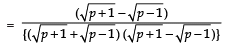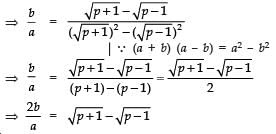Class 10 Maths Chapter 1 Question Answers - Real Numbers - 2
Ques 1: Prove that 5-2√3 is an irrational number.
Sol:
Let 5-2√3 is a rational number
∴ 5-2√3= p/q where p and q are co-prime integers and q ≠ 0.
Since, p and q are integers.
∴ p/2q is a rational number
i.e.,is a rational number.
⇒√3 is a rational number.
But this contradicts the fact that √3 is an irrational number.
So, our assumption that (5-2√3) is a rational number is not correct.
∴ (5-2√3) is an irrational number.
Ques 2: Prove that (5+3√2) is an irrational number.
Sol:
Let (5+3√2) is a rational number.
∴ (5+3√2) = a/b [where ‘a’ and ‘b’ are co-prime integers and b ≠ 0⇒
⇒
⇒‘a’ and ‘b’ are integers,
∴is a rational number.
⇒ √2 is a rational number.
But this contradicts the fact that √2 is an irrational number.
∴ Our assumption that (5+3√2) is a rational is incorrect.
⇒ (5+3√2) is an irrational number.
Ques 3: Prove that 1/√3 is irrational.

Ques 4: Consider the numbers 4n , where n is a natural number. Check whether there is any value of n for which 4n ends with the digit zero.
Sol:
If the number 4n , for any n, were to end with the digit zero, then it would be divisible by 5.
That is, the prime factorisation of 4n would contain the prime 5.
This is not possible because 4n = (2)2n ; so the only prime in the factorisation of 4n is 2.
So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorisation of 4n .
So, there is no natural number n for which 4n ends with the digit zero.
Ques 5: Prove that 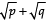 is irrational, where p and q are primes.
is irrational, where p and q are primes.
Sol:
Let
be rational
Let it be equal to ‘r’
i.e.
Squaring both sides, we have
⇒
⇒...(i)
Since, p, q are both rationals
Also, r2 is rational (∵ r is rational)
∴ RHS of (i) is a rational number
⇒ LHS of (i) should be rational i.e.√q should be rational.
But √q is irrational (∵ p is prime).
∴ We have arrived at a contradiction.
Thus, our supposition is wrong.
Hence, √p+√q is irrational.
Ques 6: Show that (2+√5 )is an irrational number.
Sol:
Let (2+√5) is a rational number.
∴ (2+√5) = p/q , such that p and q are co-prime integers and q ≠ 0
p and q are integers.
∴is a rational.
⇒ √5 is a rational.
But, this contradicts the fact that √5 is an irrational.
∴ Our supposition that (2+√5) is rational is incorrect.
Thus,(2+√5)is an irrational.
Ques 7: Prove that 3-√5 is an irrational number.
Sol:
Let (3-√5) is a rational number.
∴ 3-√5 = p/q , such that p and q are co-prime integers and q ≠ 0.⇒
⇒Since, p and q are integers,
∴is a rational number.
⇒ √5 is a rational number.
But this contradicts the fact that √5 is an irrational number.
∴ Our assumption that (3-√5) is a rational number’ is incorrect.
⇒ (3-√5) is an irrational number.
Ques 8: If ‘n’ in an integer, then show that n2 – 1 is divisible by 8.
Sol:
Le q be an integer, then
4q + 1 or 4q + 3
Now,
Case-I: When
n = 4q + 1
∴ n2 = (4q + 1)2 = 16q2 + 8q + 1
⇒ n2 – 1 = 16q2 + 8q + 1 – 1
= 16q2 + 8q
= 8q (2q + 1), which is divisible by 8.
⇒ n2 – 1 is divisible by 8.Case-II: When
n = 4q + 3
∴ n2 = (4q + 3)2 = 16q2 + 24q + 9
⇒ n2 – 1= 16q2 + 24q + 9 – 1 = 16q2 + 24q + 8
= 8(2q2 + 3q + 1) which is divisible by 8.
⇒ n2 – 1 is divisible by 8.
Thus, (n2 – 1) is divisible by 8.
Ques 9: Prove that if x and y are both odd positive integers, then x2 + y2 is even but not divisible by 4.
Sol:
Let ‘q’ be an integer, then any odd positive integer is of the form 2q + 1
Again let for some integers m and n are such that
x = 2m + 1 and y = 2n + 1
∴ x2 + y2 = (2m + 1)2 + (2n + 1)2
= 4m2 + 4m + 1 + 4n2 +4n + 1
= 4(m2 + n2) + 4
(m + n) + 2
= 4[(m2 + n2) + (m + n)] + 2
= 4q + 2
[Where q = (m2 + n2) + (m + n)]
⇒ x2 + y2 = 2[2q + 1], which an even number
Thus, 4q + 2 is an even number that is not divisible by 4, i.e. it leaves remainder 2.
Hence, x2 + y2 is even but not divisible by 4.
Ques10: Find the HCF and LCM of 6, 72 and 120, using the prime factorisation method.
Sol :
We have : 6 = 2 × 3, 72 = 23 × 32 , 120 = 23 × 3 × 5
Here, 21 and 31 are the smallest powers of the common factors 2 and 3, respectively.
So, HCF (6, 72, 120) = 21 × 31 = 2 × 3 = 6 23 , 32 and 51 are the greatest powers of the prime factors 2, 3 and 5 respectively involved in the three numbers.
So, LCM (6, 72, 120) = 23 × 32 × 51 = 360
Ques 11: Show that there is no positive integer ‘p’ for which 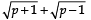 is rational.
is rational.
Sol:
If possible let there be a positive integer p for which
= a/b is equal to a rational i.e. where a and b are positive integers.
Now
Also,
Since a, b are integer
are rationals
⇒ (p + 1) and (p – 1) are perfect squares of positive integers, which is not possible (because any two perfect squares differ at least by 3). Hence, there is no positive integer p for which
is rational.
Ques 12: Show that one and only one of n, n + 2 and n + 4 is divisible by 3.
Sol:
Let us divide n by 3.
Let us get ‘q’ as quotient and ‘r’ remainder.
∴ n = 3 × q + r,where 0 ≤ r < 3
i.e., r = 0, 1, 2
when r = 0, then n = 3q ... (1)
when r = 1, then n = 3q + 1 ... (2)
when r = 2, then n = 3q + 2 ... (3)
From (1), n is divisible by 3
From (2), n = 3q + 1
Adding 2 to both sides, we have
n + 2 = (3q + 1) + 2
⇒ n + 2 = 3q + 3
⇒ n + 2 = 3 (q + 1)
3 (q + 1) is divisible by 3,
∴ n + 2 is divisible by 3.
From (3),
n = 3q + 2
Adding 4 to both sides,
(n + 4) = (3q + 2) + 4
⇒ n + 4 = 3q + 6 = 3 (q + 2)
3 (q + 2) is divisible by 3.
∴ n + 4 is divisible by 3.
At one time, r has only one value out of 0, 1, 2. Hence, only one of n, n + 2, n + 4 is divisible by 3.
OR
Let q be an integer such that 3q, (3q + 1) or (3q + 2) is a positive integer. Let us consider the following cases :
Case-I: When n = 3q
3q ÷ 3, gives 0 as remainder
∴ n = 3q is divisible by 3.
Next n = 3q ⇒ n + 2 = 3q + 2
(3q + 2) ÷ 3, gives 2 as remainder.
⇒ n + 2 = (3q + 2) is not divisible by 3.
Again, n = 3q ⇒ n + 4 = 3q + 4 = (3q + 3) + 1
∴ [(3q + 3) + 1] ÷ 3, gives 1 as remainder.
⇒ n + 4 = (3q + 4) is not divisible by 3.
Thus, n is divisible by 3, but (n + 2) and (n + 4) are not divisible by 3Case-II: When n = 3q + 1
Since (3q + 1) ÷ 3, gives remainder as 1.
∴ n = (3q + 1) is not divisible by 3.
Next, n + 2 = (3q + 1) + 2 = (3q + 3) + 0
[(3q + 3) + 0] ÷ 3, gives remainder as 0
⇒ n + 2 = (3q + 1) + 2 is divisible by 3.
Again, n = (3q + 1) ⇒ n + 4 = (3q + 1) + 4 = (3q + 3) + 2
[(3q + 3) + 2] ÷ 3, gives remainder as 2
⇒ n + 4 = (3q + 1) + 4 is not divisible by 3.
Thus, (n + 2) is divisible by 3, but n and (n + 4) are not divisible by 3Case-III: When n = 3q + 2
Since (3q + 2) ÷ 3, gives remainder as 2
∴ n = 3q + 2 is not divisible by 3
Next n + 2 = (3q + 2) + 2 = (3q + 3) + 1
[(3q + 3) + 1] ÷ 3, gives remainder as 1.
⇒ n + 2 = (3q + 2) + 2 is not divisible by 3
Again, n = 3q + 2 ⇒ n + 4 = (3q + 2) + 4 = (3q + 6) + 0
[(3q + 6) + 0] ÷ 3, gives remainder as 0
⇒ n + 4 = (3q + 2) + 4 is divisible by 3
Thus, (n + 4) is divisible by 3, but n and (n + 2) are not divisible by 3
Ques 13: Show that one and only one out of n, n + 4, n + 8, n + 12 and n + 16 is divisible by 5, where n is any positive integer.
Sol:
Let q be an integer such that 5q, (5q + 1) or (5q + 2) is a positive integer. Let us consider the following cases:
Case-I: When n = 5q
Since 5q ÷ 5, gives remainder as 0 ⇒ n is divisible by 5
Next, n = 5q ⇒ n + 4 = 5q + 4
⇒ (n + 4) is not divisible by 5
and (5q + 4) ÷ 5, gives remainder as 4
Again, n = 5q ⇒ n + 8 = 5q + 8 = (5q + 5) + 3
⇒ (n + 8) is not divisible by 5
and [(5q + 5) + 3] ÷ 5, gives remainder as 3
Similarly,
n = 5q ⇒ n + 12 = 5q + 12 = (5q + 10) + 2
⇒ (n + 12) is not divisible by 5
and [(5q + 10) + 2] ÷ 5, gives remainder as 2
n = 5q ⇒ n + 16 = 5q + 16 = (5q + 15) + 1
⇒ (n + 16) is not divisible by 5
and [(5q + 15) + 1] ÷ 5, gives remainder as 1
Thus, n is divisible by 5, but (n + 4), (n + 8), (n + 12) and (n + 16) are not divisible by 5.Case-II: When n = (5q + 1)
Here, (5q + 1) ÷ 5, gives remainder as 1 ⇒ n is not divisible by 5
Next n = (5q + 1)
⇒ n + 4 = (5q + 1) + 4 = (5q + 5) + 0
⇒ (n + 4) is divisible by 5
and [(5q + 5) + 0] ÷ 5, gives remainder as 0
Similarly,
n = (5q + 1) ⇒ n + 8 = (5q + 1) + 8
= (5q + 5) + 4
⇒ (n + 8) is not divisible by 5
and [(5q + 5) + 4] ÷ 5 gives remainder as 4
n = (5q + 1) ⇒ n + 12 = (5q + 1) + 12
= (5q + 10) + 3
⇒ (n + 12) is not divisible by 5
and [(5q + 10) + 3] ÷ 5, gives remainder as 3
n = 5q + 1 ⇒ n + 16 = 5q + 1 + 16
= (5q + 15) + 2
⇒ (n + 16) is not divisible by 5
and [(5q + 15) + 2] ÷ 5, gives remainder as 2
Thus, (n + 4) is divisible by 5, but n, (n + 8), (n + 12) and (n + 16) are not divisible by 5.Case-III: When n = (5q + 2)
Here, (5q + 2) ÷ 5, gives remainder as 2
⇒ n is not divisible by 5
Next n = 5q + 2 ⇒ n + 4 = 5q + 2 + 4
⇒ 5q + 6 = (5q + 5) + 1
⇒ (n + 4) is not divisible by 5
and [(5q + 5) + 1] ÷ 5, gives remainder as 1
Similarly,
n = 5q + 2 ⇒ n + 8 = 5q + 2 + 8 = 5q + 10
⇒ (n + 8) is divisible by 5
and (5q + 10) ÷ 5, gives remainder as 0
n = 5q + 2 ⇒ n + 12 = 5q + 2 + 12
= (5q + 10) + 4
⇒ (n + 12) is not divisible by 5
and [(5q + 10) + 4] ÷ 5, gives remainder as 4
n = 5q + 2 ⇒ n + 16 = 5q + 2 + 16
= (5q + 15) + 3
⇒ (n + 16) is not divisible by 5
and [(5q + 15) + 3] ÷ 5, gives remainder 3
Thus, (n + 8) is divisible by 5, but n, (n + 4) (n + 12) and (n + 16) are not divisible by 5.Case-IV: When n = (5q + 3)
Here, (5q + 3) ÷ 5, gives remainder as 3 ⇒ n is not divisible by 5.
Next n = 5q + 3 ⇒ n + 4 = (5q + 3) + 4
= (5q + 5) + 2
⇒ (n + 4) is not divisible by 5
and [(5q + 5) + 2] ÷ 5, gives remainder as 2
Similarly,
n = 5q + 3 ⇒ n + 8 = 5q + 3 + 8
= (5q + 10) + 1
⇒ (n + 8) is not divisible by 5
and [(5q + 10) +1] ÷ 5, gives remainder as 1
n = 5q + 3 ⇒ n + 12 = 5q + 3 + 12
= (5q + 15) + 0
⇒ (n + 12) is divisible by 5
and [(5q + 15) + 0] ÷ 5, gives remainder as 0
n = 5q + 3 ⇒ n + 16 = 5q + 3 + 16
= (5q + 15) + 4
⇒ (n + 16) is not divisible by 5
and [(5q + 15) + 4] ÷ 5, gives remainder as 4
Thus, (n + 16) is divisible by 5 but n, (n + 4) , (n + 8) and (n + 12) are not divisible by 5.Case-V: When n = (5q + 4)
Here, (5q + 4) ÷ 5, gives remainder as 4 ⇒ n is not divisible by 5
Next, n = (5q + 4) ⇒ n + 4 = 5q + 4 + 4
= (5q + 5) + 3
⇒ (n + 4) is not divisible by 5
and [(5q + 5) + 3] ÷ 5, gives remainder as 3
Similarly,
n = 5q + 4 ⇒ n + 8 = 5q + 4 + 8
= (5q + 10) + 2
⇒ (n + 8) is not divisible by 5
and [(5q + 10) + 2] ÷ 5, gives remainder as 2
n = 5q + 4 ⇒ n + 12 = 5q + 4 + 12
= (5q + 15) + 1
⇒ (n + 12) is not divisible by 5
and [(5q + 15) + 1] ÷ 5, gives remainder as 1
n = 5q + 4 ⇒ n + 16 = 5q + 4 + 16
= (5q + 20) + 0
⇒ (n + 16) is divisible by 5
and [(5q + 20) + 0] ÷ 5, gives remainder 0
Thus, (n + 16) is divisible by 5, but n, n + 4, n + 8 and n + 12 are not divisible by 5.
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 1 Question Answers - Real Numbers - 2
| 1. What are real numbers and how are they classified? |  |
| 2. How do you perform basic operations with real numbers? |  |
| 3. What are the properties of real numbers? |  |
| 4. How can real numbers be represented on a number line? |  |
| 5. What is the significance of irrational numbers in real numbers? |  |