Class 10 Maths Chapter 11 Question Answers - Surface Areas and Volumes
Q1: The radii for the top as well as the bottom of a bucket for the slant height of 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is?
Ans: Slant height of the bucket = 45 cm
Top radius is = r1 = 28cm
Bottom radius is = r2 = 7cm
Curved surface area of the bucket is = πl(r1+r2)
=22/7 * 45 * (28+7)
= 22/7 *45 *35
=4950cm2
Q2. If two identical solid cubes of side ‘x’ are joined end to end, then the total surface area of the resulting cuboid is 12x2. Is it true?
Ans: ∵ The total surface area of a cube of side x is 6x2
When they are joined end to end, the length becomes 2x
∴Total surface area
= 2[lh + bh + hl]
= 2 [(2x · x) + (x · x) + (2x · x)]
= 2 [2x2 + x2 + 2x2]
= 2 [5x2] = 10x2 ≠ 12x2
∴ False
Q3. If a solid cone of base radius ‘r’ and height ‘h’ is placed over a solid cylinder having same base radius ‘r’ and height ‘h’ as that of the cone, then the curved surface area of the shape is Is it true?
Ans: ∵ Curved surface area of a cone 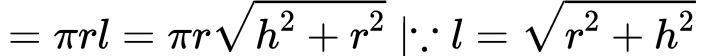
And curved surface area of the cylinder = 2πrh
∴ The curved surface area of the combination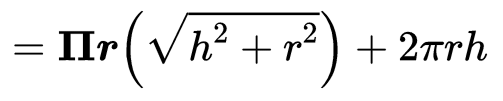
∴ True.
Q4. A cylinder and a cone are of the same base radius and same height. Find the ratio of the volumes of the cylinder of that of the cone.
Ans: Let the base radius = r and height = h
⇒ The required ratio = 3: 1
Q5: If two solid hemispheres for the same base radius r are joined together along with their bases, what is the curved surface area of this new solid?
Ans: The radius of the hemisphere = r
We know curved surface area = 2πr2
The curved surface area of two solid hemisphere
= 2 * 2πr2
= 4πr2
Q6: Vol. and surface area of a solid hemisphere are numerically equal. What is diameter of hemisphere?
Ans:
Vol. of hemisphere = S. A. of solid hemisphere 2 ,
⇒ 23πr2 = 3πr2
⇒ r = 92
∴ diameter = 2r = 9 units
Q7: Volumes for two spheres are in the ratio 64: 27. The ratio for their surface areas is?
Ans: Assume two-sphere having radius r1 and r2
As per the question,
volume of the first sphere / volume of the second sphere = 64/27
= (4/3 *πr13)/ (4/3 *πr23) = 64/27
(r1/r2)3 = 64/27
r1/r2 = 3√(64/27) =4/3
Ratio for their surface area is = (4 *πr12)/ (4 *πr22) = r12/r22 = (r1/r2)2 = (4 /3)2 = 16/9
So, the required ratio is 16:9
Q8: Two cones have their heights in the ratio 1 : 3 and radii in the ratio 3 : 1. What is the ratio of their volumes?
Ans: Given,
Ratio of heights of two cones = 1 : 3
Ratio of radii = 3 : 1
Let h and 3h be the height of two cones.
Also, 3r and r be the corresponding radii of cones.
So, r1 = 3r, h1 = h, r2 = r, h2 = 3h.
Ratio of volumes = [(1/3)πr12h1]/ [(1/3)πr22h2]
= [(3r)2 h]/[r2 (3h)] = (9r2h)/(3r2h)
= 3/1
Hence, the ratio of volumes = 3:1
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 11 Question Answers - Surface Areas and Volumes
| 1. What is the formula for calculating the surface area of a sphere? |  |
| 2. How do you find the volume of a cylinder? |  |
| 3. What is the difference between surface area and volume? |  |
| 4. How can I calculate the surface area of a rectangular prism? |  |
| 5. What is the formula for the volume of a cone? |  |
















