Class 10 Maths Chapter 11 Question Answers - Surface Areas and Volumes
| Table of contents |

|
| Q1. Frustum of a Cone |

|
| Q2. Circus Tent Canvas Area |

|
| Q3. Weight of an Iron Pillar |

|
| Q4. Building with Hemispherical Dome |

|
| Q5. Toy: Hemisphere + Cone |

|
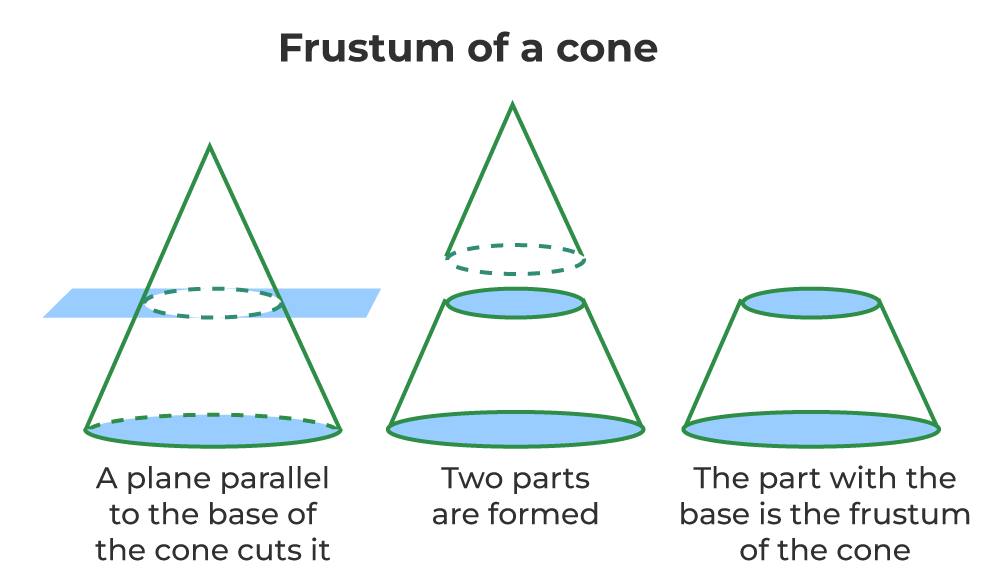
Q1. Frustum of a Cone
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume is 1/27th of the volume of the given cone, at what height above the base is the section made?
Sol. In the figure, we have ΔABC ~ ΔADE
[By AA similarity]
⇒
[∵ corresponding sides of similar Δs are proportional.]
⇒ ...(1)
Here, volume of the small cone =
Volume of the given cone =
Since, [Volume of the small cone] = 1/27
[Volume of the given cone]
∴The required height BD = AD − AB = (30 − 10) cm = 20 cm
Q2. Circus Tent Canvas Area
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and slant height of the conical portion is 53 m, find the area of the canvas needed to make the tent. [Use π = 22/7]
Sol. For cylindrical part:
We have, radius (r) = 52.5 m
Height (h)=3 m
Curved surface area = 2πrh
For the conical part
Slant height (l) = 53 m
Radius (r) = 52.5 m
∴Curved surface area = πrl
Area of the canvas = 2πrh + πrl
= πr (2h + l)
= 11 × 15 × 59 m2 = 9735 m2
Q3. Weight of an Iron Pillar
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part in 36 cm high. Find the weight of the pillar if one cu. cm of iron weighs 7.8 grams.
Sol. Here, height of the cylindrical part h = 240 cm
Height of the conical part, H = 36 cm
Radius r =8 cm
Now, the total volume of the pillar
Q4. Building with Hemispherical Dome
A building is in the form of a cylinder surmounted by a hemispherical dome as shown in the figure. The base diameter of the dome is equal to 2/3 of the total height of the building. Find the height of the building, if it contains of air.
Sol. Here, radius of the hemispherical part = r (say)
Let the total height of the building = h
And the height of the cylindrical part = H
But, volume of the air in the building
Thus, the required height of the building is 6 metres.
Q5. Toy: Hemisphere + Cone
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 4 cm and diameter of the base is 8 cm. Determine the volume of the toy. If the cube circumscribes the toy, then find the difference of the volumes of the cube and the toy. Also, find the total surface area of the toy.
Sol. Let the radius of the hemisphere = r
And height of the cone = h
Since, the cube circumscribing the given solid must have its edge as (4 + 4) cm i.e., 8 cm,
∴ Volume of the cube =(edge)3 = (8)3 cm3 = 512 cm3
Now, the difference in volumes of the cube and the toy
Also, total surface area of the toy
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 11 Question Answers - Surface Areas and Volumes
| 1. What is the formula for finding the surface area of a cube? |  |
| 2. How do you calculate the volume of a cylinder? |  |
| 3. What is the difference between lateral surface area and total surface area of a cone? |  |
| 4. How do you find the volume of a sphere? |  |
| 5. Can you explain how to find the surface area of a triangular pyramid? |  |





















