Class 10 Maths Chapter 2 Question Answers - Polynomials
Q1: Find the value of “p” from the polynomial x2 + 3x + p, if one of the zeroes of the polynomial is 2.
Ans: As 2 is the zero of the polynomial.
We know that if α is a zero of the polynomial p(x), then p(α) = 0
Substituting x = 2 in x2 + 3x + p,
⇒ 22 + 3(2) + p = 0
⇒ 4 + 6 + p = 0
⇒ 10 + p = 0
⇒ p = -10
Q2: Compute the zeroes of the polynomial 4x2 – 4x – 8. Also, establish a relationship between the zeroes and coefficients.
Ans: Let the given polynomial be p(x) = 4x2 – 4x – 8
To find the zeroes, take p(x) = 0
Now, factorise the equation 4x2 – 4x – 8 = 0
4x2 – 4x – 8 = 0
4(x2 – x – 2) = 0
x2 – x – 2 = 0
x2 – 2x + x – 2 = 0
x(x – 2) + 1(x – 2) = 0
(x – 2)(x + 1) = 0
x = 2, x = -1
So, the roots of 4x2 – 4x – 8 are -1 and 2.
Relation between the sum of zeroes and coefficients:
-1 + 2 = 1 = -(-4)/4 i.e. (- coefficient of x/ coefficient of x2)
Relation between the product of zeroes and coefficients:
(-1) × 2 = -2 = -8/4 i.e (constant/coefficient of x2)
Q3: Find the quadratic polynomial if its zeroes are 0, √5.
Ans: A quadratic polynomial can be written using the sum and product of its zeroes as:
x2 – (α + β)x + αβ
Where α and β are the roots of the polynomial.
Here, α = 0 and β = √5
So, the polynomial will be:
x2 – (0 + √5)x + 0(√5)
= x2 – √5x
Q4: Find the value of “x” in the polynomial 2a2 + 2xa + 5a + 10 if (a + x) is one of its factors.
Ans: Let f(a) = 2a2 + 2xa + 5a + 10
Since, (a + x) is a factor of 2a2 + 2xa + 5a + 10, f(-x) = 0
So, f(-x) = 2x2 – 2x2 – 5x + 10 = 0
-5x + 10 = 0
5x = 10
x = 10/5
Therefore, x = 2
Q5: How many zeros does the polynomial (x – 3)2 – 4 have? Also, find its zeroes.
Ans: Given polynomial is (x – 3)2 – 4
Now, expand this expression.
=> x2 + 9 – 6x – 4
= x2 – 6x + 5
As the polynomial has a degree of 2, the number of zeroes will be 2.
Now, solve x2 – 6x + 5 = 0 to get the roots.
So, x2 – x – 5x + 5 = 0
=> x(x – 1) -5(x – 1) = 0
=> (x – 1)(x – 5) = 0
x = 1, x = 5
So, the roots are 1 and 5.
Q6: α and β are zeroes of the quadratic polynomial x2 – 6x + y. Find the value of ‘y’ if 3α + 2β = 20.
Ans: Let, f(x) = x² – 6x + y
From the given,
3α + 2β = 20———————(i)
From f(x),
α + β = 6———————(ii)
And,
αβ = y———————(iii)
Multiply equation (ii) by 2. Then, subtract the whole equation from equation (i),
=> α = 20 – 12 = 8
Now, substitute this value in equation (ii),
=> β = 6 – 8 = -2
Substitute the values of α and β in equation (iii) to get the value of y, such as;
y = αβ = (8)(-2) = -16
Q7: Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes, respectively.
(i) 1/4, -1
(ii) 1, 1
(iii) 4, 1
Ans:
(i) From the formulas of sum and product of zeroes, we know,
Sum of zeroes = α + β
Product of zeroes = αβ
Given,
Sum of zeroes = 1/4
Product of zeroes = -1
Therefore, if α and β are zeroes of any quadratic polynomial, then the polynomial can be written as:-
x2 – (α + β)x + αβ
= x2 – (1/4)x + (-1)
= 4x2 – x – 4
Thus, 4x2 – x – 4 is the required quadratic polynomial.
(ii) Given,
Sum of zeroes = 1 = α + β
Product of zeroes = 1 = αβ
Therefore, if α and β are zeroes of any quadratic polynomial, then the polynomial can be written as:-
x2 – (α + β)x + αβ
= x2 – x + 1
Thus, x2 – x + 1 is the quadratic polynomial.
(iii) Given,
Sum of zeroes, α + β = 4
Product of zeroes, αβ = 1
Therefore, if α and β are zeroes of any quadratic polynomial, then the polynomial can be written as:-
x2 – (α + β)x + αβ
= x2 – 4x + 1
Thus, x2 – 4x +1 is the quadratic polynomial.
Q8: Find a quadratic polynomial whose zeroes are reciprocals of the zeroes of the polynomial f(x) = ax2 + bx + c, a ≠ 0, c ≠ 0.
Ans: Let α and β be the zeroes of the polynomial f(x) = ax2 + bx + c.
So, α + β = -b/a
αβ = c/a
According to the given, 1/α and 1/β are the zeroes of the required quadratic polynomial.
Now, the sum of zeroes = (1/α) + (1/β)
= (α + β)/αβ
= (-b/a)/ (c/a)
= -b/c
Product of two zeroes = (1/α) (1/β)
= 1/αβ
= 1/(c/a)
= a/c
The required quadratic polynomial = k[x2 – (sum of zeroes)x + (product of zeroes)]
= k[x2 – (-b/c)x + (a/c)]
= k[x2 + (b/c)x + (a/c)]
Q9: If α and β are zereos of the polynomial 2x2 – 5x + 7, then find the value of α-1 + β-1.
Ans: Here p(x) = 2x2 – 5x + 7
α, β are zeroes of p(x)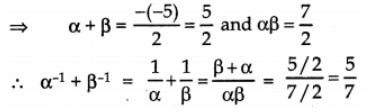
Q10: If p and q are the roots of ax2 – bx + c = 0, a ≠ 0, then find the value of p + q.
Ans: Here, p and q are the roots of ax2 – bx + c = 0.
Sum of roots = -b/a
∴ p + q = -b/a
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 2 Question Answers - Polynomials
| 1. What are polynomials and how are they classified? |  |
| 2. How do you add and subtract polynomials? |  |
| 3. What is the degree of a polynomial and how is it determined? |  |
| 4. How can you multiply polynomials using the distributive property? |  |
| 5. Can polynomials have negative exponents? |  |






















