Class 10 Maths Chapter 5 Practice Question Answers - Arithmetic Progressions

Questions

1. Find the value of ‘p’ if the numbers x, 2x + p, 3x + p are three successive terms of the AP.

2. Find p and q such that: 2p,  2p + q,  p + 4q, 35 are in AP 

3. Find a, b and c such that the following numbers are in A.P.
a, 7, b, 23, c      

Hint:
7 – a = b – 7 ⇒ a + b = 14
23 – b = b – 7 ⇒ 2b = 30  ⇒ b = 15
23 – b = c – 23  ⇒ c + b = 4 6 ⇒ c = 46 – b
= 46 – 15

=31

And a = 14 – b = 14 – 15 = – 1
4. Determine k so that k² + 4k + 8, 2k² + 3k + 6, 3k² + 4k + 4 are three consecutive terms of an AP.

5. 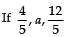 are three consecutive terms of an AP, find the value of a.

6. For what value of p, are (2p – 1), 7 and 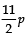 three consecutive terms of an AP?

7. If (x + 2), 2x, (2x + 4) are three consecutive terms of an AP, find the value of x.

8. For what value of p are (2p – 1), 13 and (5p – 10) are three consecutive terms of an A.P.?

9. Find the 10th term from the end of the A.P. 4, 9, 14, ... 254. 

10. Find the 6th term of the AP 54, 51, 48... 

11. Find the 8th term from the end of the AP : 7, 10, 13, ..., 184. 

12. Find the 16th term of the AP 3, 5, 7, 9, 11, ... 

13. Find the 12th term of the AP:
14, 9, 4, –1, –6, ...

14. Find the middle term of the AP :
20, 16, ..., –180

15. Find the 6th term from the end of the A.P.
17, 14, 11, ..., (–40)

16. Find the middle term of the AP :
10, 7, 4, ..., (–62)

17. Which term of the AP : 24, 21, 18, 13, ... is the first negative term?
Hint: The first negative term will be the term immediately less than 0. i.e. Tn < 0.
⇒ [a + (n – 1)d] < 0
Here, a = 24
d = (21 - 24) = -3
⇒ 3n > 27
⇒ n > 9  
∴ n = 10
18. The 6th term of an AP is –10 and its 10th term is –26. Determine the 15th term of the A.P. 

19. For what value of n are the nth terms of the following two APs the same: 13, 19, 25, ...     and 69, 68, 67, ....

20. The 8th term of an AP is zero. Prove that its 38th term is triple its 18th term.
Hint:
T₈ =0 ⇒ a + 7d = 0 ⇒ a = –7d
T₃₈ = a + 37d = –7d + 37d = 30d
Also, T₁₈ = a + 17d = –7d + 17d = 10d
30d = 3 × (10d)  ⇒ T₃₈ = 3 × T₁₈

21. For what value of n, the nth terms of the following two AP’s are equal?
23, 25, 27, 29, ... and –17, –10, –3, 4, ...

22. Which term of the AP : 5, 15, 25, ... will be 130 more than 31st term?
Hint: Let an be the required term
i.e. an be 130 more than a₃₁ 
⇒ a_n – a₃₁ = 130

23. Which term of the AP : 3, 15, 27, 39, ... will be 130 120 more than its 64th term? 

24. The 9th term of an AP is 499 and its 499th term is 9. Which of its term is equal to zero.

25. Determine A.P. whose fourth term is 18 and the difference of the ninth term from fifteenth term is 30. 

26. How many natural numbers are there between 200 and 500 which are divisible by 7?
Hint: 200  ... 203 ... 497     ... 500
← Divisible by 7 →
∴   a = 203,  d = 7   and a_n = 497
⇒  a + (n – 1) d = a_n ⇒ 203 + (n – 1) × 7 = 497
27. How many multiples of 7 are there between 100 and 300? 

28. Find the value of the middle term of the following A.P. : –11, –7, –3, ..., 49. 

29. Find the value of the middle term of the following A.P. : –6, –2, 2, ..., 58. 

30. How many two digit numbers are divisible by 3?
Hint: Here, a = 12, d = 3 and an = 99

31. If the 9th term of an AP is zero, show that 29th term is double the 19th term.
Hint:
 

  ⇒   20d = 20d
⇒ a₂₉  = a₁₉

32. If in an AP, the sum of its first ten terms is –80 and the sum of its next ten terms is –280. Find the AP

33. If in an A.P. a_n = 20 and S_n = 399 then find ‘n’
Hint: a_n = a + (n – 1)d ⇒ (n – 1)d = 19

34. Find the sum of all natural numbers from 1 to 100. 

35. The first and last terms of an AP are 4 and 81 respectively. If the common difference is 7, how many terms are there in the A.P. and what is their sum? 

36. How many terms of A.P. a, 17, 25, ... must be taken to get a sum of 450? 

37. Find the sum of first hundred even natural numbers which are multiples of 5. 

38. Find the sum of the first 30 positive integers divisible by 6. 

39. Find the sum of those integers from 1 to 500 which are multiples of 2 or 5.
Hint: Multiples of 2 are : 2, 4, 6, 8, 10, 12, 14, 16, ..., 500.

Multiples of 5 are : 5, 10, 15, 20, 25, 30, ..., 500.

Multiples of 2 as well as 5 : 10, 20, 30, 40, ..., 500. ∴ The required sum
= [Sum of multiplies of 2] +[S um of multiples of 5]-[ Multiples of 2 as we]

40. If the nth term of an A.P. is 2n + 1, find Sn of the A.P. 

41. An A.P. consists of 37 terms. The sum of the three middle most terms is 225 and the sum of the last three terms is 429. Find the A.P. 

42. If S_n denotes the sum of n-terms of A.P. whose common differences is d and first term is a find: S_n – 2S_n–1 + S_n–2 
Hint: a_n = S_n – S_n–1 

43. If the ratio of 11th term to 18th term of an A.P. is 2 : 3. Find the ratio of the 5th term to the 21st term and also the ratio of the sum of the first five terms to the sum of first 21 terms.

44. If in an A.P. the first term is 2, the last term is 29 and sum of the terms is 155. Find the common difference of the A.P.

45. The sum of n terms of an A.P. is  Find the 20th term.

46. If Sn denotes the  sum of first n terms of an A.P., prove that
S₃₀ = 3(S₂₀ – S₁₀)

47. The 4^th term of an A.P. is zero. Prove that the 25^th term of the A.P. is three times its 11^th term.

48. Find the 9^th term from the end (towards the first term) of A.P. 5, 9, 13, .........185.

49. How many terms of the A.P. 18, 16, 14, ......... be taken so that their sum is zero?

Answer

1. p = 0 

2. p = 10, q = 5 

3. a = –1, b = 15, c = 31 

4. k = 0 

5. a = 8/5 

6. p = 2 

7. x = 6 

8. p = 5 

9. 209 

10. 69 

11. 163 

12. 33

13. –41 

14. –80 

15. –25 

16. –26

17. n = 10 

18. –46 

19. n = 9 

21. n = 9 

22. 44th 

23. 74th 

24. 508 

25. 3, 8, 13, 18, ... 

26. 43 

27. 28 

28. 17; 21 

29. 26

30. 30 

32. 1, –1, –3, –5, –7... 

33. 38

34. 5050 

35. 12, 510 

36. 10 

37. 50500

38. 2790 

39. 27250 

40. n(n + 2) 

41. 3, 7, 11, 15, ... 

42. d 

43. 1 : 3; 5 : 49 

44. d = 3 

45. 99 

48. 153 

49. n = 19