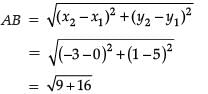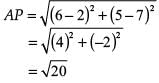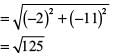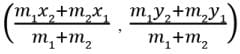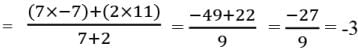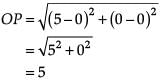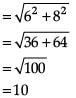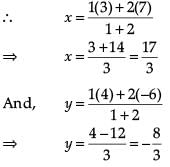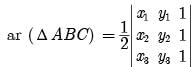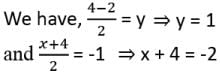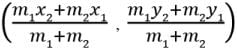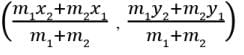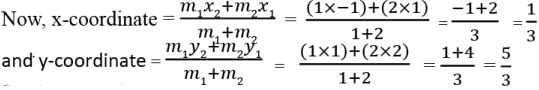Q1:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The ordinate of a point A on y-axis is 5 and B has coordinates (–3, 1). Then the length of AB is 5 units.
Reason (R): The point A(2, 7) lies on the perpendicular bisector of line segment joining the points P(6, 5) and Q(0, –4).
Explanation
In case of assertion
Here, A → (0 , 5) and B → (– 3 , 1)
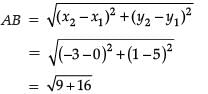
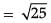
= 5 units
∴ Assertion is correct.
In case of reason: If A (2, 7) lies on perpendicular bisector of P (6, 5) and Q (0, –4), then
AP = AQ
∴ By using Distance Formula,
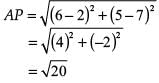
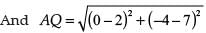
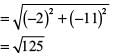
As, AP ≠ AQ
Therefore, A does not lie on the perpendicular bisector of PQ.
∴ Reason is incorrect.
Hence, assertion is correct but reason is incorrect.
Report a problem
Q2:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself:Directions: In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion: The area of the triangle with vertices (-5, -1), (3, -5), and (5, 2) is 32 square units.
Reason: The point (x, y) divides the line segment joining the points (x1, y1) and (x2, y2) in the ratio k : 1 externally, then
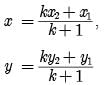
Explanation
Using the formula for area of triangle using coordinates,

and section formula (externally), we have

Report a problem
Q3:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The co-ordinates of the point which divides the join of A(-5, 11) and B(4,-7) in the ratio 7 : 2 is (2, -3) Reason : The coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) in the ratio m1 : m2 is 
Explanation
We know that the coordinates of the point P(x, y) which divides the line segment joining the points A(x
1, y
1) and B(x
2, y
2) in the ratio m
1 : m
2 is
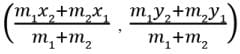
So, Reason is correct.
Here, x1 = -5, y1 = 11, x2 = 4, y2 = -7, m1 = 7, m2 = 2
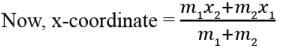
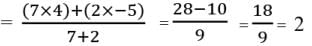
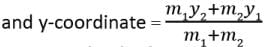
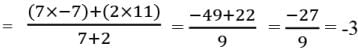
So, Assertion is also correct
Report a problem
Q4:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): △ABC with vertices A(–2, 0), B(2, 0) and C(0, 2) is similar to △DEF with vertices D(–4, 0), E(4, 0) and F(0, 4).
Reason (R): A circle has its centre at the origin and a point P(5, 0) lies on it. The point Q(6, 8) lies outside the circle.
Explanation
In case of assertion: By using Distance Formula,
∴ Distance between A (-2, 0) and B (2, 0),
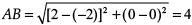
[∵ distance between the points (x1, y1) and (x2, y2)

Similarly, distance between B (2, 0) and C (0, 2),
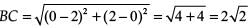
In △ABC, distance between C (0, 2) and A (-2, 0),
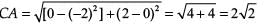
Distance between F (0, 4) and D (–4, 0),
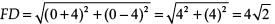
Distance between F (0, 4) and E (4, 0),
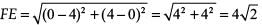
and distance between E (4, 0) and D (–4, 0),
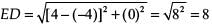
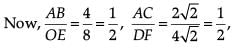
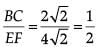
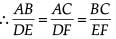
Here, we see that sides of DABC and DFDE are proportional.
Therefore, by SSS similarity rule, both the triangles are similar.
∴ Assertion is correct.
In case of reason: Point Q (6, 8) will lie outside the circle if its distance from the centre of circle is greater than the radius of the circle.
Distance between centre O (0, 0) and P (5, 0),
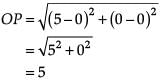
As, point P lies at the circle, therefore, OP = Radius of circle.
Distance between centre O (0, 0) and Q (6, 8),
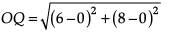
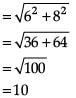
As OQ > OP, therefore, point Q (6, 8) lies outside of the circle.
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Report a problem
Q5:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The points (k, 2 -2k), (- k+ 1,2k) and (- 4 - k, 6 - 2k) are collinear if k = 1/2. Reason : Three points A,B and C are collinear in same straight line, if AB + BC = AC.
Explanation
Consider the given points.
(−k + 1, 2k), (k, 2 − 2k),(−4 −k, 6 − 2k)
Since, these points are collinear. Therefore the area of triangle formed by the triangle formed by the points will be zero.
Therefore,
(−k + 1)(2 − 2k − 6 + 2k) + k(6 − 2k − 2k) + (−4 − k)(2k − 2 + 2k) = 0
(−k + 1)(−4) + k(6 − 4k) + (−4 − k)(4k − 2) = 0
4k − 4 + 6k − 4k2 − 16k + 8 − 4k2 + 2k = 0
−2k2 − k + 1 = 0
2k2 + k − 1 = 0
2k2 + 2k − k − 1 = 0
2k(k + 1) − 1(k + 1) = 0
(k + 1)(2k − 1) = 0
k = −1 or k = 1/2.
Report a problem
Q6:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : If the points A(4, 3) and B(x, 5) lies on a circle with the centre O(2,3) then the value of x is 2.
Reason : The mid-point of the line segment joining the points P(x1, y1) and Q(x2, y2) is
Explanation
We know that the mid-point of the line segment joining the points P(x
1, y
1) and Q(x
2, y
2) is
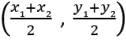
So, Reason is correct.
Given, the points A (4,3) and B (x, 5) lie on a circle with center O(2,3).
Then OA = OB ⇒(OA)2 = (OB)2
⇒ (4 – 2)2 + (3 – 3)2 = (x – 2)2 + (5 – 3)2
⇒ (2)2 +(0)2 = (x – 2)2 + (2)2 ⇒ 4 = (x – 2)2 + 4 ⇒(x – 2)2 = 0
⇒ x – 2 = 0 ⇒ x = 2
So, Assertion is correct
Report a problem
Q7:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If the distance between the point (4, p) and (1, 0) is 5, then the value of p is 4.
Reason (R): The point which divides the line segment joining the points (7, – 6) and (3, 4) in ratio 1 : 2 internally lies in the fourth quadrant.
Explanation
In case of assertion: Distance between two points (x
1, y
1) and (x
2, y
2) is given as,
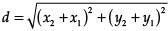
where, (x1, y1) = (4, p)
(x2, y2) = (1, 0)
And, d = 5
Put the values, we have
52 = (1 − 4)2 + (0 – p)2
25 = (–3)2 + (–p)2
25 – 9 = p2
16 = p2
+4, –4 = p
∴ Assertion is incorrect.
In case of reason:
Let (x, y) be the point
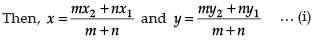
Here, x1 = 7, y1 = –6, x2 = 3, y2 = 4, m = 1 and n = 2
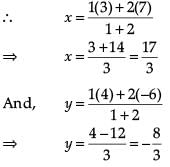
So, the required point 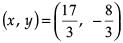 lies in IVth quadrant.
lies in IVth quadrant.
∴ Reason is correct.
Hence, assertion is incorrect but reason is correct.
Report a problem
Q8:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Centroid of a triangle formed by the points (a, b) (b, c), and (c, a) is at origin, Then a + b + c = 0 .
Reason : Centroid of a △ABC with vertices A (x1, y1), B(x2, y2) and C (x3, y3) is given by

Explanation
Centroid of a triangle with vertices (a, b) (b, c), and (c, a) is
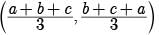
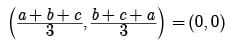
a + b + c = 0
Report a problem
Q9:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The possible values of x for which the distance between the points A(x, -1) and B(5, 3) is 5 units are 2 and 8.
Reason : Distance between two given points A(x1, y1) and B(x2, y2) is given by,

Explanation
We know that the Distance between two given points A(x
1, y
1) and B(x
2, y
2) is given by,

So, Reason is correct.
Now, AB = 5 ⇒ AB2 = 25
⇒ (x – 5)2 + (-1 - 3)2 = 25
⇒ (x – 5)2 = 25 – 16 = 9
⇒ x – 5 = ±3
⇒ x = 5 ± 3
⇒ x = 2, 8
So, Assertion is also correct
Report a problem
Q10:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Mid-point of a line segment divides line in the ratio 1 : 1.
Reason : If area of triangle is zero that means points are collinear.
Explanation
Let us assume that point B divides the line AC in the ratio k : 1
Let(x1, y1, z1) = (0, 0, 0)
(x, y ,z) = (2, −3, 3)
(x2, y2, z2) = (−2, 3, −3)
By section formula:
x = m1 + m2 m1 x 2 + m2 x 1
⇒ 2 = k + 1 k.(−2) + 1.(0)
⇒ k = 4 − 1 on neglecting the negative sign
we get, therefore ratio is 1:4.
Report a problem
Q11:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The point (-1, 6) divides the line segment joining the points (-3, 10) and (6, -8) in the ratio 2 : 7 internally.
Reason : Three points A,B and C are collinear if AB + BC = AC
Explanation
We know that the three points A,B and C are collinear if AB + BC = AC
So, Reason is correct.
Let the ratio is k : 1. Here, x1 = -3, y1 = 10, x2 = 6, y2 = -8, x = -1, y = 6
Now, y-coordinate
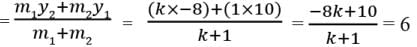
⇒ -8k + 10 = 6k + 6
⇒ 10 – 6 = 6k + 8k
⇒ 14k = 4
⇒ k = 4/14 = 2/7
So, Assertion is correct
But reason (R) is not the correct explanation of assertion (A).
Report a problem
Q12:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The point (-1, 6) divides the line segment joining the points (-3, 10) and (6, -8) in the ratio 2 :7 internally.
Reason : Three points A,B and C are collinear if area of △ ABC = 0 .
Explanation
Using section formula, we have
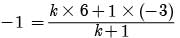
- k- 1 = 6k -3
7k = 2
k = 2/7
Ratio be 2 :7 internally.
Also, if ar(△ ABC) = 0
A,B and C all these points are collinear.
Report a problem
Q13:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The value of y is 6, for which the distance between the points P(2,- 3) and Q(10, y) is 10.
Reason : Distance between two given points A(x1, y1) and B(x2, y2) is given by,
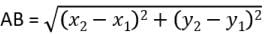
Explanation
We know that the Distance between two given points A(x1, y1) and B(x2, y2) is given by,

So, Reason is correct.
Now, PQ = 10 ⇒ PQ2 = 100
⇒ (10 – 2)2 + (y + 3)2 = 100
⇒ (y + 3)2 = 100 – 64 = 36
⇒ y + 3 = ±6
⇒ y = -3 ± 6 ⇒ y = 3, -9
So, Assertion is not correct
Report a problem
Q14:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : If A (2a, 4a) and B (2a, 6a) are two vertices of a equilateral triangle ABC then the vertex C is given by (2a + a√3, 5a).
Reason : In equilateral triangle all the coordinates of three vertices can be rational.
Explanation
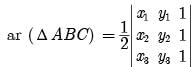

LHS = rational
RHS = irrational
Hence, (x1, y1) (x2, y2) and (x3, y3) cannot be all rational.
Report a problem
Q15:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The point (0, 4) lies on y -axis.
Reason : The x co-ordinate on the point on y -axis is zero.
Explanation
We know that the if the point lies on y-axis, its x-coordinate is 0.
So, Reason is correct.
The x co-ordinate of the point (0, 4) is zero.
So, Point (0, 4) lies on y -axis.
So, Assertion is also correct
Report a problem
Q16:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The value of y is 6, for which the distance between the points P(2, -3) and Q(10, y) is 10.
Reason : Distance between two given points A (x1, y1) and B(x2, y2) is given 6,
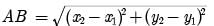
Explanation
PQ = 10
PQ2 = 100
(10 - 2)2 + (y + 3)2 = 100
(y + 3)2 = 100 - 64 = 36
y + 3 = + 6
y = - 3 + 6
y = 3, -9
Report a problem
Q17:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : C is the mid-point of PQ, if P is (4, x), C is (y,- 1) and Q is (- 2, 4), then x and y respectively are -6 and 1.
Reason : The mid-point of the line segment joining the points P(x1, y1) and Q(x2, y2) is 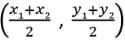
Explanation
We know that the mid-point of the line segment joining the points P(x
1, y
1) and Q(x
2, y
2) is
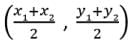
So, Reason is correct.
Since, C(y,- 1) is the mid-point of P(4, x) and Q(- 2, 4).
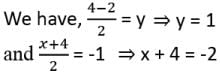
⇒ x = -6
So, Assertion is correct
Report a problem
Q18:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The point (0, 4) lies on y -axis.
Reason : The x co-ordinate on the point on y -axis is zero.
Explanation
The x co-ordinate of the point (0, 4) is zero.
Point (0, 4) lies on y -axis.
Report a problem
Q19:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Ratio in which the line 3x + 4y = 7 divides the line segment joining the points (1, 2) and (- 2, 1) is 3 : 5Reason : The coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) in the ratio m1 : m2 is 
Explanation
We know that the coordinates of the point P(x, y) which divides the line segment joining the points A(x
1, y
1) and B(x
2, y
2) in the ratio m
1 : m
2 is
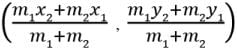
So, Reason is correct.
Let the ratio is k : 1.
Here, x1 = 1, y1 = 2, x2 = -2, y2 = 1, m1 = k, m2 = 1
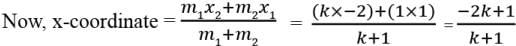
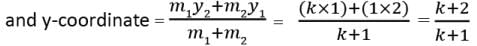
Now, 3x + 4y = 7
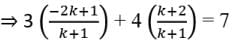
⇒ 7k + 2k = 11 – 7 ⇒ 9k = 4 ⇒ k = 4/9
So, Assertion is not correct
Report a problem
Q20:
Question for Assertion & Reason Type Questions: Coordinate Geometry
Try yourself:Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion: The point which divides the line joining the points A(1, 2) and B(- 1, 1) internally in the ratio 1: 2 is 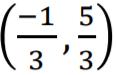
Reason : The coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) in the ratio m1 : m2 is

Explanation
We know that the coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) in the ratio m1 : m2 is
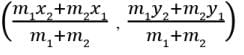
So, Reason is correct.
Here, x1 = 1, y1 = 2, x2 = -1, y2 = 1, m1 = 1, m2 = 2
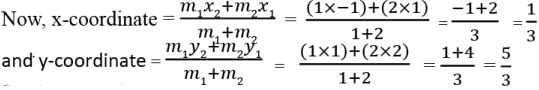
So, Assertion is correct.
Report a problem
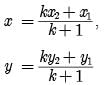

![]()
![]()
![]()
![]()
![]()
![]()