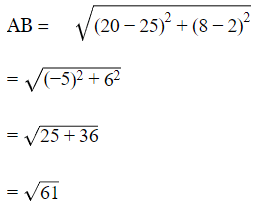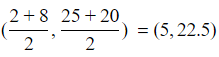Q1: The points A(-4, -1), B(-2, -4), C(4, 0) and D(2, 3) are the vertices of a-
(a) Parallelogram
(b) Rectangle
(c) Rhombus
(d) Square
Ans: (b)
For a rectangle, the opposite sides need to be equal and diagonals also have to be equal.
Now by using
Distance Formula = 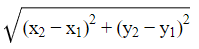
Here coordinates of A are x1 and y1
and coordinates of B are x2 and y2
Similarly for other coordinates also. Length AB=

= √13
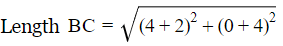
= √52
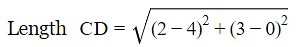
= √13
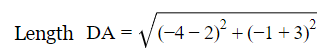
= √52
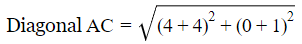
= √65
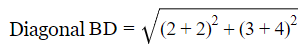
= √65
ABCD are the vertices of a rectangle since AB=DC and AD = BC, also diagonal AC = BD.
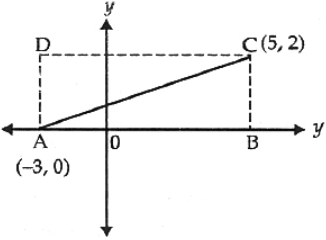
Q2: If A (−3,0) and C (5,2) are the end points of diagonal AC of rectangle ABCD, with B on the x- axis, the perimeter of the rectangle ABCD is
(a) 20
(b) 24
(c) 28
(d) 30
Ans: (a)
Both A & B i.e the side AB lies on the X-axis.
Again BC⊥AB ...(since □ ABCD is a rectangle)
⇒ Abscissa of B= abscissa of C.
∴ B = (x,0) = (5,0) .... [since C=(5,2) ]
∴ Length AB = difference beteen abscissae of A & B = [(5−(−3)] = 8 units.
Again length BC= difference beteen ordinates of B & C=(2−0)=2 units.
∴ The perimeter P = 2(AB + BC) = 2(8+2) = 20 sq. units.
Q3: A student moves √2x km east from his residence and then moves x km north. He then goes x km north east and finally he takes a turn of 90∘ towards right and moves a distance x km and reaches his school. What is the shortest distance of the school from his residence?
(a) (2√2 +1)x km
(b) 3x km
(c) 2√2x km
(d) 3√2x km
Ans: (b)
In triangle BCD
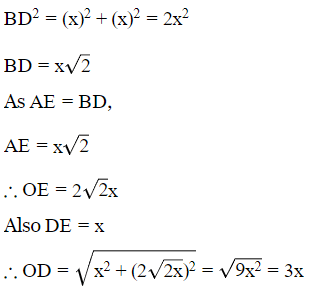
Q4: A(3,4) and B(5,−2) are two given points. If AP=PB and area of △P AB = 10, then P is
(a) (7,1)
(b) (7,2)
(c) (−7,2)
(d) (−7,−1)
Ans: (b)
Let the coordinate P be (x,y)
Since it is given that PA = PB
So, by using distance formula
P(x, y) and A(3, 4)
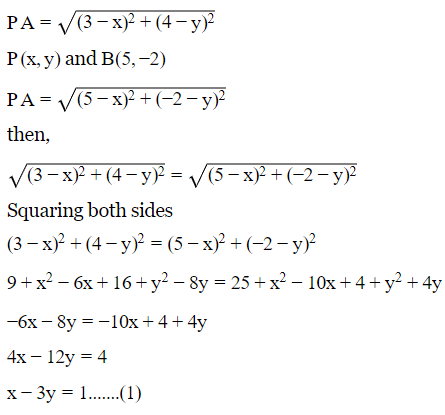
Area of △P AB = 10
Area of triangle of (3,4),(5,-2) and (x,y)
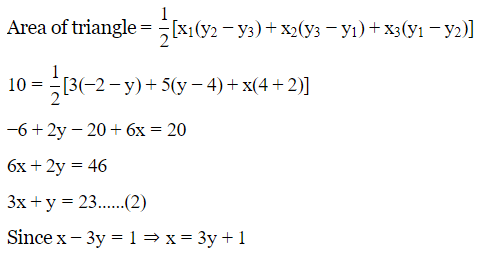
Equation (2) implies
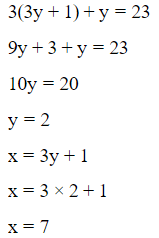
Therefore, the coordinates are (7, 2).
Q5: Show that the following point taken in order form the vertices of a rhombus.
(2, -3), (6, 5), (-2, 1) and (-6, -7)
Ans: Consider the given points.
(2, -3), (6, 5), (-2, 1) and (-6, -7)

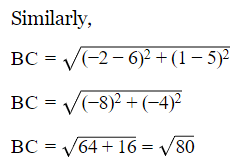
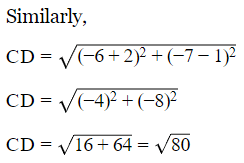
Therefore,
AB = BC = CD = AD
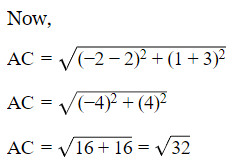
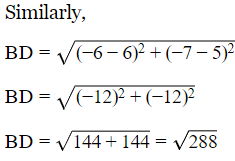
So,
AC=BD
As all the sides are equal and diagonals are not equal.
Its shows that the following vertices are of rhombus.
Hence, this is the answer.
Q6: The coordinates of the point Q on the x-axis lies on the perpendicular bisector of the line segment joining the points A(5,2) and B(4,2). Name the type of triangle formed by the points Q,A and B.
(a) Equilateral
(b) Isosceles
(c) Scalene
(d) None of these
Ans: The point Q lies on the x-axis. So, its co-ordinate will be of the form (x,0) Let's take the points as Q(x,y) = (x,0) which is equidistant from A(5,2) and B(4,2) To find the distance, we use distance formula
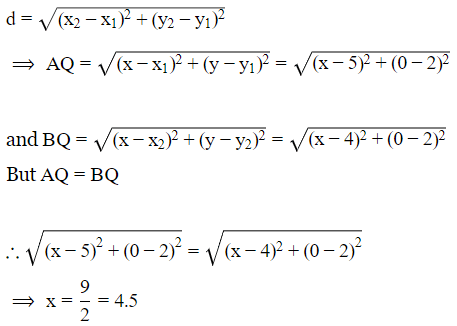
∴ The co-ordinates of Q is (4.5,0)
∵ AQ = BQ and Q lies on the perpendicular bisector of AB
Therefore, the ΔABQ is an isosceles triangle.
Q7: To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Fig. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5 th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?
 Ans: AD = 100 m and AB = 10m
Ans: AD = 100 m and AB = 10m
The coordinates of Niharika's flag = (2,25) and the coordinates of Preet's flag = (8,20).
A(2,25) and B(8,20)
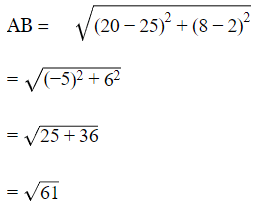
Distance between both flags is √61 m.
Rashmi has to place her flag at the midpoint of AB.
MIdpoint of AB = 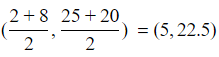
Rashmi must place her flag along the fifth line at 22.5 m from A.
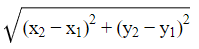

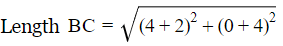
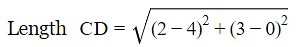
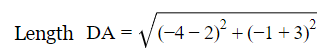
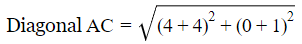
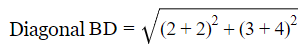

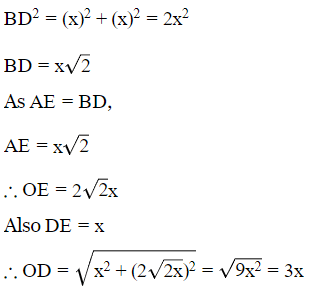
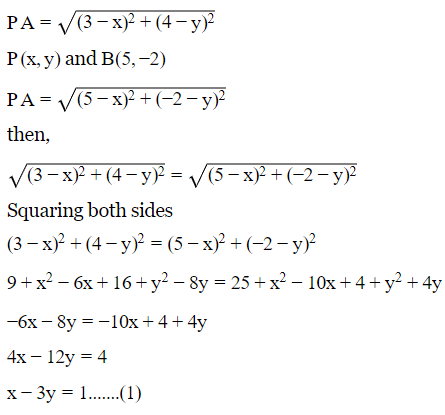
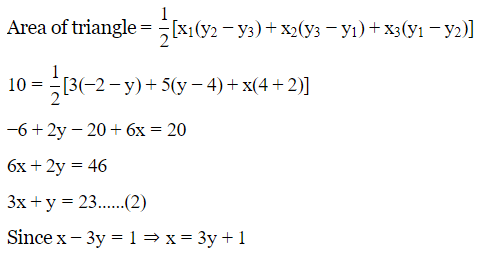
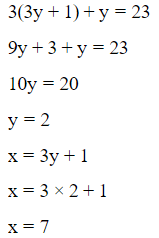

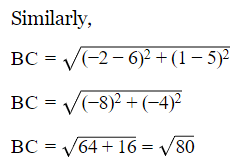
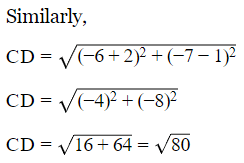
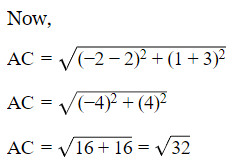
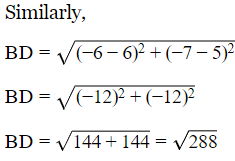
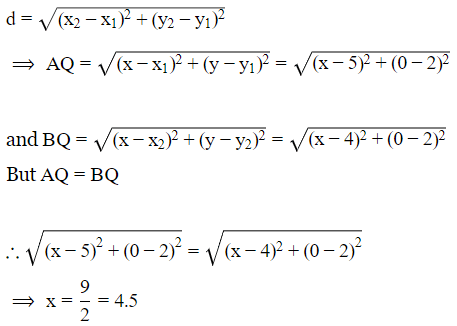
 Ans: AD = 100 m and AB = 10m
Ans: AD = 100 m and AB = 10m