Class 10 Maths Chapter 7 Practice Question Answers - Coordinate Geometry
Q1. Find the distance of the point P (2, 3) from the x-axis.
Sol:
We know that,
(x, y) = (2, 3) is a point on the Cartesian plane in the first quadrant.
x = Perpendicular distance from y-axis
y = Perpendicular distance from x-axis
Therefore, the perpendicular distance from x-axis = y coordinate = 3
Q 2. Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Sol:
Let P(x, y) be equidistant from the points A(7, 1) and B(3, 5).
Then, AP = BP
AP2 = BP2
Using distance formula,
(x – 7)2 + (y – 1)2 = (x – 3)2 + (y – 5)2
x2 – 14x + 49 + y2 – 2y + 1 = x2 – 6x + 9 + y2 – 10y + 25
x – y = 2
Hence, the relation between x and y is x – y = 2.
Q.3. Find the coordinates of the points of trisection (i.e., points dividing into three equal parts) of the line segment joining the points A(2, – 2) and B(– 7, 4).
Sol:
Let P and Q be the points of trisection of AB, i.e., AP = PQ = QB.
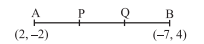
Therefore, P divides AB internally in the ratio 1: 2.
Let (x1, y1) = (2, -2)
(x2, y2) = (-7, 4)
m1 : m2 = 1 : 2
Therefore, the coordinates of P, by applying the section formula,
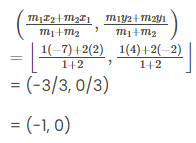
Similarly, Q also divides AB internally in the ratio 2 : 1. and the coordinates of Q by applying the section formula,

Hence, the coordinates of the points of trisection of the line segment joining A and B are (–1, 0) and (– 4, 2).
Q4. Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).
Sol:
Let the ratio in which the line segment joining ( -3, 10) and (6, -8) is divided by point ( -1, 6) be k:1.
Therefore by section formula,
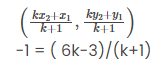
–k – 1 = 6k -3
7k = 2
k = 2/7
Hence, the required ratio is 2 : 7.
Q 5. Find the value of k if the points A(2, 3), B(4, k) and C(6, –3) are collinear.
Sol:
Given,
A(2, 3)= (x1, y1)
B(4, k) = (x2, y2)
C(6, -3) = (x3, y3)
If the given points are collinear, the area of the triangle formed by them will be 0.
½ [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
½ [2(k + 3) + 4(-3 -3) + 6(3 – k)] = 0
½ [2k + 6 – 24 + 18 – 6k] = 0
½ (-4k) = 0
4k = 0
k = 0
Q6. Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Sol:
Let the vertices of the triangle be A(0, -1), B(2, 1) and C(0, 3).
Let D, E, F be the mid-points of the sides of this triangle.
Using the mid-point formula, coordinates of D, E, and F are:
D = [(0+2)/2, (-1+1)/2] = (1, 0)
E = [(0+0)/2, (-1+3)/2] = (0, 1)
F = [(0+2)/2, (3+1)/2] = (1, 2)
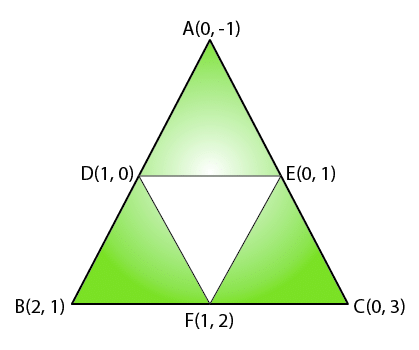
We know that,
Area of triangle = ½ [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
Area of triangle DEF = ½ {(1(2 – 1) + 1(1 – 0) + 0(0 – 2)}
= ½ (1 + 1)
= 1
Area of triangle DEF = 1 sq.unit
Area of triangle ABC = ½ {0(1 – 3) + 2(3 – (-1)) + 0(-1 – 1)}
= ½ (8)
= 4
Area of triangle ABC = 4 sq.units
Hence, the ratio of the area of triangle DEF and ABC = 1 : 4.
Q7. Name the type of triangle formed by the points A (–5, 6), B (–4, –2) and C (7, 5).
Sol:
The points are A (–5, 6), B (–4, –2) and C (7, 5).
Using distance formula,
d = √ ((x2 – x1)2 + (y2 – y1)2)
AB = √((-4+5)² + (-2-6)²)
= √(1+64)
=√65
BC=√((7+4)² + (5+2)²)
=√(121 + 49)
=√170
AC=√((7+5)² + (5-6)²)
=√144 + 1
=√145
Since all sides are of different lengths, ABC is a scalene triangle.
Q8. Find the area of triangle PQR formed by the points P(-5, 7), Q(-4, -5) and R(4, 5).
Sol:
Given,
P(-5, 7), Q(-4, -5) and R(4, 5)
Let P(-5, 7) = (x1, y1)
Q(-4, -5) = (x2, y2)
R(4, 5) = (x3, y3)
Area of the triangle PQR = (½)|x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|
= (½) |-5(-5 – 5) + (-4)(5 – 7) + 4(7 + 5)|
= (½) |-5(-10) -4(-2) + 4(12)|
= (½) |50 + 8 + 48|
= (½) × 106
= 53
Therefore, the area of triangle PQR is 53 sq. units.
Q9. If the point C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3 : 4, find the coordinates of B.
Sol:
Given,
C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3 : 4.
Here,
A(2, 5) = (x1, y1)
B(x, y) = (x2, y2)
m : n = 3 : 4
Using section formula,
C(-1, 2) = [(mx2 + nx1)/(m + n), (my2 + ny1)/(m + n)]
= [(3x + 8)/(3 + 4), (3y + 20)/(3 + 7)]
By equating the corresponding coordinates,
(3x + 8)/7 = -1
3x + 8 = -7
3x = -7 – 8
3x = -15
x = -5
And
(3y + 20)/7 = 2
3y + 20 = 14
3y = 14 – 20
3y = -6
y = -2
Therefore, the coordinates of B(x, y) = (-5, -2).
Q10. Find the ratio in which the line x – 3y = 0 divides the line segment joining the points (-2, -5) and (6, 3). Find the coordinates of the point of intersection.
Sol:
Let the given points be:
A(-2, -5) = (x1, y1)
B(6, 3) = (x2, y2)
The line x – 3y = 0 divides the line segment joining the points A and B in the ratio k : 1.
Using section formula,
Point of division P(x, y) = [(kx2 + x1)/(k + 1), (ky2 + y1)/(k + 1)]
x = (6k – 2)/(k + 1) and y = (3k – 5)/(k + 1)
Here, the point of division lies on the line x – 3y = 0.
Thus,
[(6k – 2)/(k + 1)] – 3[(3k – 5)/(k + 1)] = 0
6k – 2 – 3(3k – 5) = 0
6k – 2 – 9k + 15 = 0
-3k + 13 = 0
-3k = -13
k = 13/3
Thus, the ratio in which the line x – 3y = 0 divides the line segment AB is 13 : 3.
Therefore, x = [6(13/3) – 2]/ [(13/3) + 1]
= (78 – 6)/(13 + 3)
= 72/16
= 9/2
And
y = [3(13/3) – 5]/ [(13/3) + 1]
= (39 – 15)/(13 + 3)
= 24/16
= 3/2
Therefore, the coordinates of the point of intersection = (9/2, 3/2).
Q11. Write the coordinates of a point on the x-axis which is equidistant from points A(-2, 0) and B(6, 0).
Sol:
Let P(x, 0) be a point on the x-axis.
Given that point, P is equidistant from points A(-2, 0) and B(6, 0).
AP = BP
Squaring on both sides,
(AP)² = (BP)²
Using distance formula,
(x + 2)² + (0 – 0)² = (x – 6)² + (0 – 0)²
x² + 4x + 4 = x² – 12x + 36
4x + 12x = 36 – 4
16x = 32
x = 2
Therefore, the coordinates of a point on the x-axis = (2, 0).
Q12. If A(-2, 1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram ABCD, find the values of a and b. Hence, find the lengths of its sides.
Sol:
Given vertices of a parallelogram ABCD are:
A(-2, 1), B(a, 0), C(4, b) and D(1, 2)
We know that the diagonals of a parallelogram bisect each other.
So, midpoint of AC = midpoint of BD
[(-2 + 4)/2, (1 + b)/2] = [(a + 1)/2, (0 + 2)/2]
By equating the corresponding coordinates,
2/2 = (a + 1)/2 and (1 + b)/2 = 2/2
a + 1 = 2 and b + 1 = 2
a = 1 and b = 1
Therefore, a = 1 and b = 1.
Let us find the lengths of sides of a parallelogram, i.e. AB, BC, CD and DA
Using the distance formula,
AB = √[(1 + 2)² + (0 – 1)²] = √(9 + 1) = √10 units
BC = √[(4 – 1)² + (1 – 0)²] = √(9 + 1) = √10 units
And CD = √10 and DA = √10 {the opposite sides of a parallelogram are parallel and equal}
Hence, the length of each side of the parallelogram ABCD = √10 units.
Q.13: If A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
Sol:
Given vertices of a quadrilateral are:
A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5)
The quadrilateral ABCD can be divided into two triangles ABD and BCD.
Area of the triangle with vertices (x1, y1), (x2, y2), and (x3, y3) = (½) |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|
Area of triangle ABD = (½) |-5(-5 – 5) + (-4)(5 – 7) + 4(7 + 5)|
= (½) |-5(-10) -4(-2) + 4(12)|
= (½) |50 + 8 + 48|
= (½) × 106
= 53
Area of triangle BCD = (½) |-4(-6 – 5) + (-1)(5 + 5) + 4(-5 + 6)|
= (½) |-4(-11) -1(10) + 4(1)|
= (½) |44 – 10 + 4|
= (½) × 38
= 19
Therefore, the area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD
= 53 + 19
= 72 sq.units
Q14. Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, -3). Hence, find m.
Sol:
Let P(4, m) divides the line segment joining the points A(2, 3) and B(6, -3) in the ratio k : 1.
Here,
P(4, m) = (x, y)
A(2, 3) = (x1, y1)
B(6, -3) = (x2, y2)
Using section formula,
p(x, y) = [(kx2 + x1)/(k + 1), (ky2 + y1)/(k + 1)]
(4, m) = [(6k + 2)/(k + 1), (-3k + 3)/(k + 1)]
By equating the x-coodinate,
(6k + 2)/(k + 1) = 4
6k + 2 = 4k + 4
6k – 4k = 4 – 2
2k = 2
k = 1
Thus, the point P divides the line segment joining A and B in the ratio 1 : 1.
Now by equating the y-coodinate,
(-3k + 3)/(k + 1) = m
Substituting k = 1,
[-3(1) + 3]/(1 + 1) = m
m = (3 – 3)/2
m = 0
Q15. Find the distance of a point P(x, y) from the origin.
Sol:
Given,
P(x, y)
Coordinates of origin = O(0, 0)
Let P(x, y) = (x1, y1)
O(0, 0) = (x2, y2)
Using distance formula,
OP = √[(x2 – x1)² + (y2 – y1)²]
= √[(x – 0)² + (y – 0)²]
= √(x² + y²)
Hence, the distance of the point P(x, y) from the origin is √(x² + y²) units.
|
127 videos|584 docs|79 tests
|





















