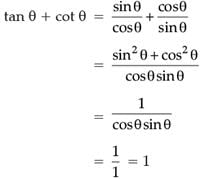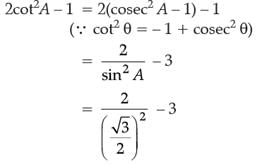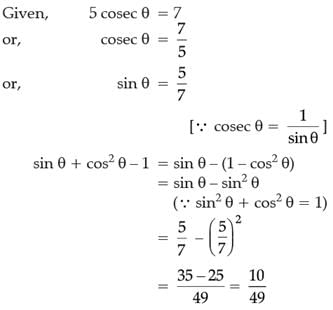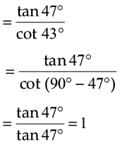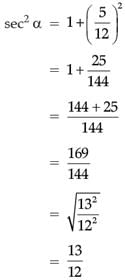Q1:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : The value of sin θ = 4/3 in not possible.
Reason : Hypotenuse is the largest side in any right angled triangle.
Explanation
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
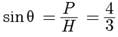
Here, the perpendicular is greater than the hypotenuse which is not possible in any right triangle.
Report a problem
Q2:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion: The value of sec210o - cot280o is 1
Reason: The value of sin 30o = 1/2
Explanation
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
We have,
sec2 10° - cot2 80° = sec2 10° - cot2(90° - 10°)
= sec2 10° — tan2 10° = 1
Also, sin30° = 1/2
Report a problem
Q3:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : In a right angled triangle, if tanθ = 3/4, the greatest side of the triangle is 5 units.
Reason: (greatest side)2 = (hypotenuse)2 = (perpendicular)2 + (base) 2.
Explanation
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A). Both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
Greatest side =
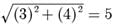 units.
units.
Report a problem
Q4:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : In a right angled triangle, if cosθ = 1/2 and sinθ = √3/2, then tanθ = √3
Reason: tanθ = sinθ/cosθ
Explanation
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A). Both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
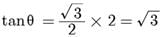
Report a problem
Q5:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): Cot A is the product of Cot and A.
Reason (R): The value of sinq increases as q increases.
Explanation
In case of assertion
cot A is not the product of cot and A. It is the cotangent of ∠A.
∴ Assertion is incorrect.
In case of reason:
The value of sin q increases as q increases in interval of θ°< θ°="" />< />
∴ Reason is correct:
Hence, the assertion is incorrect but the reason is correct.
Report a problem
Q6:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If tan A = cot B, then the value of (A + B) is 90°.
Reason (R): If sec θ sin θ = 0, then the value of q is 0°.
Explanation
In case of assertion
tan A = cot B (Given)
tan A = tan(90° – B)
[∵ tan (90° - θ) = cot θ]
A = 90° – B
Hence, A + B = 90°.
∴ Assertion is correct.
In case of reason:
Given, sec θ.sin θ = 0
or,
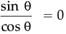
or, tan θ = 0 = tan 0°
∴ θ = 0°
∴ Reason is correct:
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Report a problem
Q7:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If k + 1 = sec2 θ (1 + sin θ) (1 – sin θ), then the value of k is 1.
Reason (R): If sin θ + cos θ = √3 then the value of tan θ + cot θ is 1.
Explanation
In case of assertion
k + 1 = sec2 θ(1 + sin θ)(1 – sin θ)
or, k + 1 = sec2 θ(1 – sin2 θ)
or, k + 1 = sec2 θ. cos2 θ
[∵ sin2 θ + cos2 θ = 1]
or,
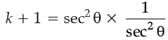
or, k + 1 = 1
or, k = 1 – 1
∴ k = 0.
∴ Assertion is incorrect.
In case of reason:
Given sin θ + cos q = √3
Squaring on both sides,
(sin θ + cos θ)2 = (√3)2
sin2 θ + cos2 θ + 2 sin θ cos θ = 3
1 + 2 sin θ cos θ = 3
2 sin θ cos θ = 2
sin θ cos θ = 1 ... (i)
∴
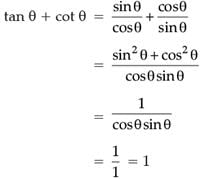
∴ Reason is correct:
Hence, Assertion is incorrect but reason is correct.
Report a problem
Q8:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If sin A = √3/2, then the value of 2 cot2 A - 1 is -1/3.
Reason (R): If q be an acute angle and 5 cosec q = 7, then the value of sin θ + cos2 θ – 1 is 10.
Explanation
In case of assertion
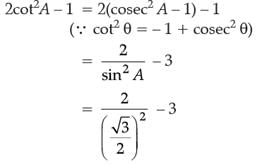
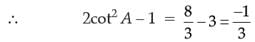
∴ Assertion is correct.
In case of reason:
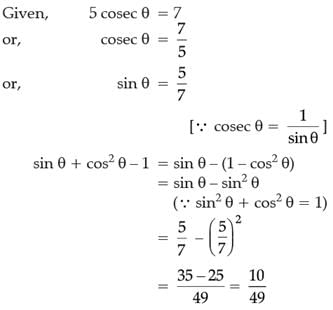
∴ Reason is incorrect:
Hence, assertion is correct but reason is incorrect.
Report a problem
Q9:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : sin2 67o + cos2 67o = 1
Reason : For any value of θ, sin2θ + cos2θ = 1
Explanation
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
sin2θ + cos2θ = 1
sin267o + cos267o = 1
Report a problem
Q10:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : sin 47° = cos 43°
Reason : sin θ = cos (90 + θ), where θ is an acute angle.
Explanation
Assertion (A) is true but reason (R) is false. Assertion is true, but reason is not correct.
sin θ = cos (90 - θ)
sin 47° = cos (90 — 47°) = cos43°
Report a problem
Q11:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : If cos A + cos2A = 1 then sin2A + sin4A = 2
Reason : 1 - sin2 A = cos2A, for any value of A.
Explanation
Assertion (A) is false but reason (R) is true.
cos A + cos2A = 1
cos A = 1 - cos2A = sin2A
sin2 A + sin4A = cos A + cos2 A = 1
sin2 A + sin4 A = 1
Report a problem
Q12:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : The value of sinθcos (90 — θ) + cos θsin (90 — 0) equals to 1.
Reason : tanθ = sec (90 — θ)
Explanation
Assertion (A) is true but reason (R) is false.
sin θ • cos (90 — θ) + cos θ sin(90 — θ)
= sin θ • sin θ + cos θ • cos θ
= sin2 θ + cos2 θ = 1
and, tan θ = cot (90 — θ)
Report a problem
Q13:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The value of tan47γ/cot43γ is 1.
Reason (R): The value of the expression (sin 80° – cos 80°) is negative.
Explanation
In case of assertion
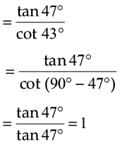
∴ Assertion is correct.
In case of reason:
80° is near to 90°, sin 90° = 1 and cos 90° = 0
So, the given expression sin 80° – cos 80° > 0
So, the value of the given expression is positive.
∴ Reason is incorrect:
Hence, the assertion is correct but the reason is incorrect.
Report a problem
Q14:
Question for Assertion & Reason Type Questions: Introduction to Trigonometry
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If x = 2 sin2 θ and y = 2 cos2 θ + 1 then the value of x + y = 3.
Reason (R): If tan α = 5/12, then the value of sec α is 13/12.
Explanation
In case of assertion
We have x = 2 sin2 θ
and y = 2 cos2 θ + 1
Then, x + y = 2 sin2 θ + 2 cos2 θ + 1
= 2(sin2 θ + cos2 θ) + 1
= 2 × 1 + 1
[∵ sin2 θ + cos2 θ = 1]
= 2 + 1 = 3.
∴ Assertion is correct.
In case of reason:
tan α = 5/12
Using identity; sec2 α – tan2 α = 1
sec2 α = 1 + tan2 α
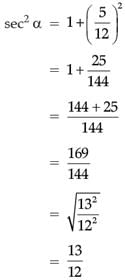
∴ Reason is correct:
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Report a problem