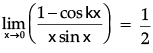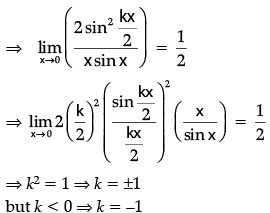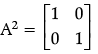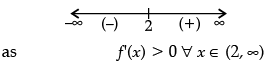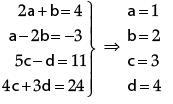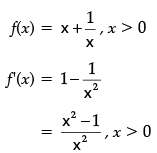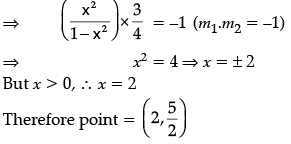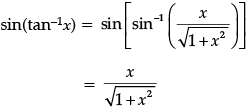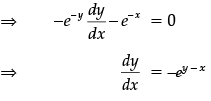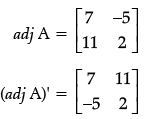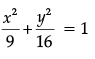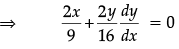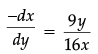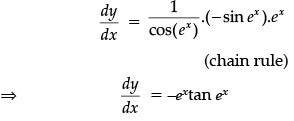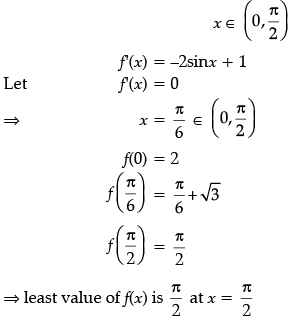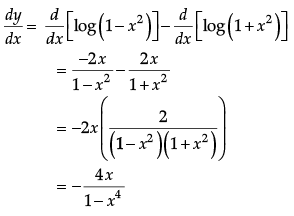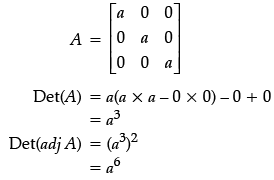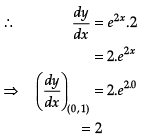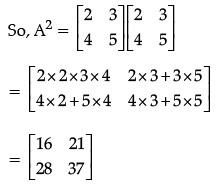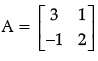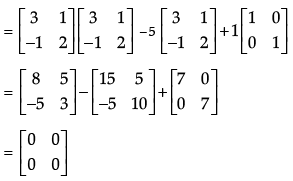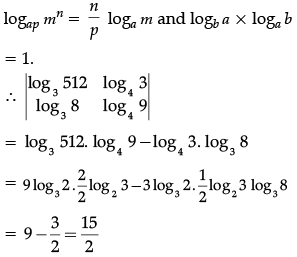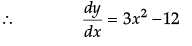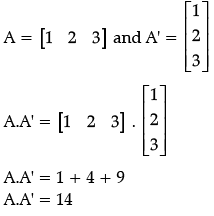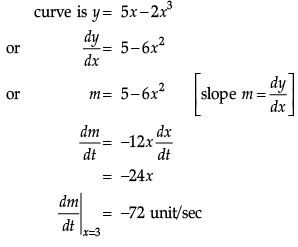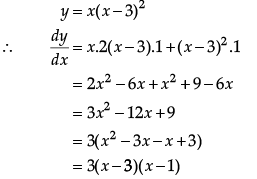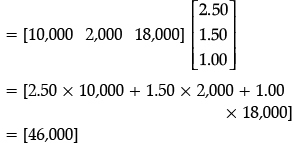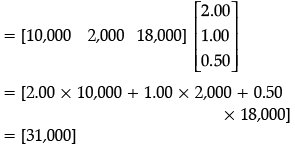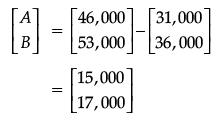Class 12 Mathematics: CBSE Sample Question Paper- Term I (2021-22)- 4 | Mathematics (Maths) Class 12 - JEE PDF Download
Class-XII
Time: 90 Minutes
Max. Marks: 40
General Instructions :
- This question paper contains three sections – A, B and C. Each part is compulsory.
- Section - A has 20 MCQs, attempt any 16 out of 20.
- Section - B has 20 MCQs, attempt any 16 out of 20.
- Section - C has 10 MCQs, attempt any 8 out of 10.
- There is no negative marking.
- All questions carry equal marks
Section - A
Q.1: 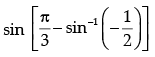 is equal to:
is equal to:
(a) 1/2
(b) 1/3
(c) –1
(d) 1
Correct Answer is Option (d)
= 1
Q.2: The value of k (k < 0) for which the function f defined as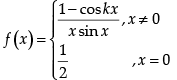
is continuous at x = 0 is:
(a) ± 1
(b) –1
(c) ±1/2
(d) 1/2
Correct Answer is Option (d)
Q.3: If A = [αij] is a square matrix of order 2 such that αij = 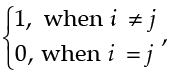 then A2 is:
then A2 is:
(a)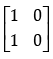
(b)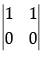
(c)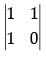
(d)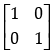
Correct Answer is Option (d)
Q.4: Value of k, for which A = 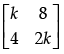 is a singular matrix is:
is a singular matrix is:
(a) 4
(b) –4
(c) ±4
(d) 0
Correct Answer is Option (c)
As A is singular matrix
⇒ |A| = 0⇒ 2k2 – 32 = 0
⇒ k = ±4
Q.5: Find the intervals in which the function f given by f(x) = x2 – 4x + 6 is strictly increasing:
(a) (– ∞, 2) ∪ (2, ∞)
(b) (2, ∞)
(c) (− ∞, 2)
(d) (– ∞, 2] ∪ (2, ∞)
Correct Answer is Option (b)
f(x) = x2 – 4x + 6
f'(x) = 2x – 4
Let f(x) = 0
⇒ x = 2
⇒ f(x) is Strictly increasing in (2, ∞)
Q.6: Given that A is a square matrix of order 3 and | A | = - 4, then | adj A | is equal to:
(a) –4
(b) 4
(c) –16
(d) 16
Correct Answer is Option (d)
as |adj A| = |A|n – 1,
where n is order of matrix A
= (–4)2 = 16
Q.7: A relation R in set A = {1, 2, 3} is defined as R = {(1, 1), (1, 2), (2, 2), (3, 3)}. Which of the following ordered pair in R shall be removed to make it an equivalence relation in A
(a) (1, 1)
(b) (1, 2)
(c) (2, 2)
(d) (3, 3)
Correct Answer is Option (b)
Q.8: If, 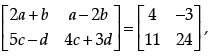 then value of a + b – c + 2d is:
then value of a + b – c + 2d is:
(a) 8
(b) 10
(c) 4
(d) –8
Correct Answer is Option (a)
∴ a + b – c + 2d = 8
Q.9: The point at which the normal to the curve y = x + 1/x, x > 0 x is perpendicular to the line 3x – 4y – 7 = 0 is:
(a) (2, 5/2)
(b) (±2, 5/2)
(c) (–1/2, 5/2)
(d) (1/2, 5/2)
Correct Answer is Option (d)
As normal to f(x) is ⊥ to given line
Q.10: sin (tan–1x), where |x| < 1, is equal to:
(a)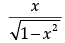
(b) 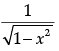
(c) 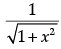
(d) 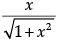
Correct Answer is Option (d)
Q.11: Let the relation R in the set A = {x ∈ Z : 0 ≤ x ≤ 12}, given by R = {(a, b) : |a – b| is a multiple of 4}. Then [1], the equivalence class containing 1, is:
(a) {1, 5, 9}
(b) {0, 1, 2, 5}
(c) ϕ
(d) A
Correct Answer is Option (a)
Q.12: If ex + ey = ex+y, then dy/dx is:
(a) ey – x
(b) ex + y
(c) –ey – x
(d) 2ex – y
Correct Answer is Option (c)
ex + ey = ex + y
⇒ e–y + e–x = 1
Differentiating w.r.t. x:
Q.13: Given that matrices A and B are of order 3 × n and m × 5 respectively, then the order of matrix C = 5A + 3B is:
(a) 3 × 5 and m = n
(b) 3 × 5
(c) 3 × 3
(d) 5 × 5
Correct Answer is Option (b)
Q.14: If y = 5 cos x – 3 sin x, then d2y/dx2 is equal to:
(a) –y
(b) y
(c) 25y
(d) 9y
Correct Answer is Option (a)
y = 5cos x – 3sin x
⇒ dy/dx = –5sin x – 3cos x⇒ d2y/dx2 = –5cos x + 3sin x
= –y
Q.15: For matrix A = 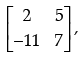 (αdj A)' is equal to:
(αdj A)' is equal to:
(a) 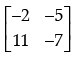
(b) 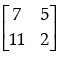
(c) 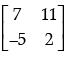
(d) 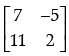
Correct Answer is Option (c)
Q.16: The points on the curve 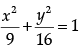 at which the tangents are parallel to y-axis are:
at which the tangents are parallel to y-axis are:
(a) (0, ±4)
(b) (±4, 0)
(c) (±3, 0)
(d) (0, ±3)
Correct Answer is Option (b)
⇒ Slope of normal =
As curve's tangent is parallel to y-axes⇒ 9y/16x = 0
⇒ y = 0 and x = ±3
∴ points = (±3, 0)
Q.17: Given that A = [aij] is a square matrix of order 3 × 3 and |A| = −7, then the value of 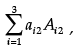 where Aij denotes the cofactor of element αij is:
where Aij denotes the cofactor of element αij is:
(a) 7
(b) –7
(c) 0
(d) 49
Correct Answer is Option (b)
|A| = –7
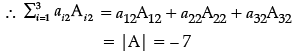
Q.18: If y = log(cos ex), then dy/dx is:
(a) cos ex−1
(b) e–x cos ex
(c) ex sin ex
(d) –ex tan ex
Correct Answer is Option (b)
y = log(cos ex)
Differentiating w.r.t. x:
Q.19: Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?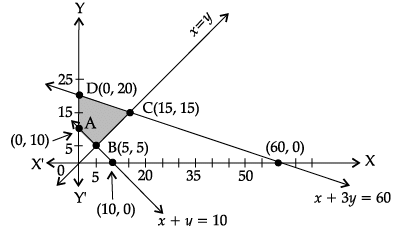
(a) Point B
(b) Point C
(c) Point D
(d) every point on the line segment CD
Correct Answer is Option (d)
Z is maximum 180 at points C (15, 15) and D(0, 20).
⇒ Z is maximum at every point on the line segment CD.
Q.20: The least value of the function f(x) = 2cos x + x in the closed interval [0, π/2] is:
(a) 2
(b) π/6 + √3
(c) π/2
(d) The least value does not exist
Correct Answer is Option (c)
f(x) = 2cos x + x,
Section - B
Q.21: Which of the following functions from Z into Z are bijections?
(a) f(x) = x3
(b) f(x) = x + 8
(c) f(x) = 4x + 1
(d) f(x) = x2 + 7
Correct Answer is Option (b)
For bijection on Z, f(x) must be one-one and onto. Function f(x) = x2 + 7 is many-one as f(1) = f(–1) Range of f(x) = x3 is not Z for x ∈ Z. Also f(x) = 4x + 1 takes only values of type = 4k + 1 for x ∈ k ∈ Z But f(x) = x + 8 takes all integral values for x ∈ Z. Hence f(x) = x + 8 is a bijection of Z.
Q.22: If  then dy/dx is equal to
then dy/dx is equal to
(a) 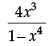
(b) 
(c) 
(d) 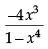
Correct Answer is Option (b)
Given that,
Differentiate with respect to x, we have
Q.23: The feasible region for an LPP is always a _______ polygon.
(a) Concave
(b) Convex
(c) Both A and B
(d) None
Correct Answer is Option (b)
The feasible region for an LPP is always a convex polygon.
Q.24: Local maximum of the function 3x 4 −20x3+36x 2 + 322 in (−10, 10) ?
(a) 2
(b) 3
(c) 0
(d) 5
Correct Answer is Option (a)
Let f(x)
= 3x4 – 20x3 +36 x2 + 322
f '(x) = 12x3 – 60x2 + 72x
Put f '(x) = 0
12x3 – 60x2 + 72x = 0
12x (x2 – 5x + 6) = 0
12x (x – 2) (x – 3) = 0
x = 0, 2, 3
f ''(x) = 36x2 – 120x + 72
f ''(0) = 72 > 0
f ''(2) = 36 × 22 – 120 × 2 + 72 = –24 < 0
f ''(3) = 36 × 32 – 120 × 3 + 72 = 36 > 0
∴ We get local maxima at x = 2.
Q.25: If the matrix A is both symmetric and skew symmetric, then
(a) A is a diagonal matrix
(b) A is a zero matrix
(c) A is a square matrix
(d) None of these
Correct Answer is Option (b)
If A is both symmetric and skew-symmetric then we have, A' = A and A' = –A
⇒ A = –A
⇒ A + A = 0
⇒ 2A = 0
⇒ A = 0
Therefore, A is a zero matrix.
Q.26: f(x) = [x] The function is:
(a) Not Continuous
(b) continuous
(c) Differentiable
(d) None of these
Correct Answer is Option (a)
L.H.L and R.H.L. are not equal at integer points.
Q.27: What is the domain of the sec–1 x ?
(a) [−∞, ∞]
(b) (−∞, ∞)
(c) (–1, 1)
(d) (−∞, −1] ∪ [1,∞)
Correct Answer is Option (d)
The sec function is periodic so to calculate its inverse function we need to make the function bijective. For that we have to consider an interval in which all values of the function exist and do not repeat. Now for the inverse of a function the domain becomes range and the range becomes domain. Thus the range of secant function, that is, (−∞,−1]∪[1,∞) becomes the domain of inverse function.
Q.28: If 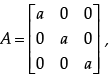 then det (adj A) equals
then det (adj A) equals
(a) a27
(b) a9
(c) a6
(d) a2
Correct Answer is Option (c)
Q.29: The tangent to the curve y = e2x at the point (0, 1) meets x-axis at :
(a) (0, 1)
(b) (-1/2, 0)
(c) (2, 0)
(d) (0, 2)
Correct Answer is Option (b)
The equation of the curve is given by y = e2x Since, it passes through the point (0, 1).
= Slope of tangent to the curve.
∴ Equation of tangent is
y - 1 = 2(x -0)
⇒ y = 2x + 1
Since, tangent to the curve y = e2x at the point (0, 1) meets x-axis, i.e., y = 0.
∴ 0 = 2x + 1
⇒ x = -1/2
So, the required point is (-1/2, 0).
Q.30: Consider the set A = {1, 3, 5, 7}. The number of reflexive relations on set A is :
(a) 212
(b) 122
(c) 24
(d) 42
Correct Answer is Option (a)
By definition, a relation in A is said to be reflexive if xRx, ∀x ∈ A.
So R is true.
The number of reflexive relations on a set containing n elements is 2 n2 -n
Here n = 4.
The number of reflexive relations on a set A = 212
Q.31: The interval on which the function f (x) = 2x3 + 9x2 + 12x- 1 is decreasing is:
(a) [–1, ∞)
(b) (–2, –1)
(c) (–∞, –2]
(d) [–1, 1]
Correct Answer is Option (c)
Given that,
f(x) = 2x3 + 9x2 + 12x - 1
f'(x) = 6x2 + 18x + 12
= 6(x2 + 3x + 2)
6(x + 2)(x + 1)So, f'(x) ≤ 0 for decreasing.
On drawing number lines as below:
We see that f '(x) is decreasing in (−2, −1).
Q.32: If A 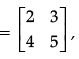 Find A2
Find A2
(a) 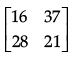
(b) 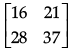
(c) 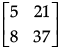
(d) None of these
Correct Answer is Option (b)
We need to find A2 and we know that A2 = A.A
Q.33: A corner point of a feasible region is a point in the region which is the __________ of two boundary lines.
(a) Intersection
(b) Disjoint
(c) Middle point
(d) None
Correct Answer is Option (a)
A corner point of a feasible region is a point in the region which is the intersection of two boundary lines.
Q.34: The function f(x) = 2x3 – 3x2 – 12x + 4, has
(a) two points of local maximum
(b) two points of local minimum
(c) one maxima and one minima
(d) no maxima or minima
Correct Answer is Option (c)
We have,
f(x) = 2x3 + 3x2 + 12x + 4
f'(x) = 6 x2 + 6x - 12
Now, f'(x) = 0
⇒ 6(x2 - x - 2) = 0
⇒ 6 (x + 1)(x - 2) = 0
⇒ x = -1 and x = +2
On number line for f’(x), we get
Hence, x = −1 is point of local maxima and x = 2 is point of local minima.
So, f(x) has one maxima and one minima.
Q.35: If A 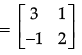 then A2 – 5A + 7I2 is equal to
then A2 – 5A + 7I2 is equal to
(a) 0
(b) 1
(c) –1
(d) 2
Correct Answer is Option (a)
Value of A2 – 5A + 7I2
Since, all the elements of matrix are zero. So, given matrix is null/zero matrix.
Q.36: The principal value of tan−1 (−√3) is:
(a) π/3
(b) - π/3
(c) 2π/3
(d) π/6
Correct Answer is Option (b)
The principal value of tan−1 (−√3) means that we need to find an angle in the principal branch of the function where the tangent function is equal to -√3 . Hence the required value is - π/3.
Q.37: The principal value of 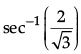 is:
is:
(a) π/3
(b) π/2
(c) π/6
(d) π/4
Correct Answer is Option (c)
The principal value of means that we need to find an angle in the principal branch of the function where the secant function is equal to 2/√3. Hence the required value is π/6.
Q.38. Evaluate the determinant 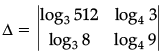
(a) –17
(b) log3 18
(c) log28
(d) 15/2
Correct Answer is Option (d)
For simplification usage of the properties of logarithm are required
Q.39: The points at which the tangents to the curve y = x3 – 12x + 18 are parallel to x-axis are:
(a) (2, 2), (–2, –34)
(b) (2, 34), (–2, 0)
(c) (0, 34), (–2, 0)
(d) (2, 2), (–2, 34)
Correct Answer is Option (d)
The equation of the curve is given by
y = x3 – 12x + 18
On differentiating with respect to x, we get
So, the slope of line parallel to the x-axis,
So, the points are (2, 2) and (−2, 34).
Q.40: If matrix A = [1 2 3]. Write A.A' where A' is the transpose of matrix A.
(a) 4
(b) 21
(c) 14
(d) 28
Correct Answer is Option (c)
Section - C
Q.41: The optimal value of the objective function is attained at the points.
(a) X-axis only
(b) Y-axis only
(c) Corner points of feasible region
(d) Origin only
Correct Answer is Option (c)
The optimal value of the objective function is attained at the corner points of feasible region.
Q.42: For the curve y = 5x – 2x3, if x increases at the rate of 2 units/sec, then at x = 3 the slope of curve is changing at ________ units/sec.
(a) –72
(b) –36
(c) 24
(d) 48
Correct Answer is Option (a)
Given
Q.43: y = x(x – 3)2 decreases for the values of x given by:
(a) 1 < x < 3
(b) x < 0
(c) x > 0
(d) 0 < x < 3/2
Correct Answer is Option (a)
Given that, y = x(x – 3)2
So, y = x(x – 3)2 decreases for (1, 3).
[Since, y' < 0 for all x ∈ (1, 3), hence y is decreasing on (1, 3)].
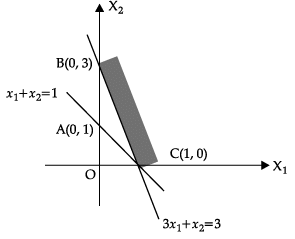
Q.44: For the constraints of linear optimizing function Z = x1 + x2 given by x1 + x2 ≤ 1, 3x1 + x2 ≥1, there is feasible region
(a) Yes
(b) No
(c) Can't be determined
(d) None of these
Correct Answer is Option (b)
Clearly from the graph below that there is no feasible region.
Q.45: Let A =  then |AB| is equal to
then |AB| is equal to
(a) 460
(b) 2000
(c) 3000
(d) – 7000
Correct Answer is Option (d)
CASE-STUDY
A manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below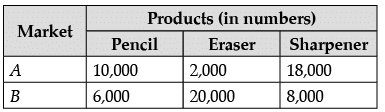
 If the unit Sale price of Pencil, Eraser and Sharpener are Rs 2.50, Rs 1.50 and Rs 1.00 respectively, and unit cost of the above three commodities are Rs 2.00, Rs 1.00 and Rs 0.50 respectively, then,
If the unit Sale price of Pencil, Eraser and Sharpener are Rs 2.50, Rs 1.50 and Rs 1.00 respectively, and unit cost of the above three commodities are Rs 2.00, Rs 1.00 and Rs 0.50 respectively, then,
Based on the given information, answer the following questions.
Q.46: Total revenue of market A
(a) Rs 64,000
(b) Rs 60,400
(c) Rs 46,000
(d) Rs 40600
Correct Answer is Option (c)
Q.47: Total revenue of market B
(a) Rs 35,000
(b) Rs 53,000
(c) Rs 50,300
(d) Rs 30,500
Correct Answer is Option (b)
= [2.50 × 6,000 + 1.50 × 20,000 + 1.00 × 8,000]
= [53,000]
Q.48: Cost incurred in market A
(a) Rs 13,000
(b) Rs 30,100
(c) Rs 10,300
(d) Rs 31,000
Correct Answer is Option (d)
Cost incurred in marker A
Q.49: Profits in market A and B respectively are
(a) (Rs 15,000, Rs 17,000)
(b) (Rs 17,000, Rs 15,000)
(c) (Rs 51,000, Rs 71,000)
(d) (Rs 10,000, Rs 20,000)
Correct Answer is Option (a)
Cost incurred in market B
Profit of market A & B = total revenue of A and B – Cost increased in market A and B
Q.50: Gross profit in both markets
(a) Rs 23,000
(b) Rs 20,300
(c) Rs 32,000
(d) Rs 30,200
Correct Answer is Option (c)
Gross profit in both markets = Profit in A + Profit in B
= 15,000 + 17,000
= Rs 32,000
|
203 videos|307 docs|139 tests
|