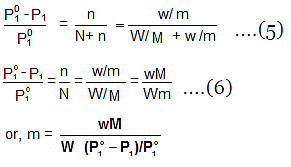Colligative Properties: Elevation in B.P., Depression in F.P., Relative Lowering in Vapour Pressure | Chemistry Class 12 - NEET PDF Download
| Table of contents |

|
| What are Colligative Properties? |

|
| 1. Boiling Point Elevation |

|
| 2. Freezing Point Depression |

|
| 3.Relative Lowering of Vapour Pressure |

|
| 4. Osmosis and Osmotic Pressure |

|
What are Colligative Properties?
The colligative properties of the solution, are the properties that are bound by the number of solute and solvent particle present in the solution. Colligative properties are features of a solution that change based on how much solute is dissolved in it, rather than what the solute or solvent are.

There are four main colligative properties
- Elevation of Boiling point
- Depression Freezing point
- Lowering of Vapour Pressure
- Osmotic Pressure
 Colligative Properties and Its Types
Colligative Properties and Its Types
Applications of Colligative Properties
Colligative properties are important in various practical applications, including in the pharmaceutical industry, food science, and chemical engineering They are also used in analytical techniques, such as osmometry, to determine the molecular weight of substances.
Note: It's important to note that colligative properties are only applicable to ideal solutions, which means that the solute-solvent interactions are relatively weak, and the solute particles do not associate or dissociate significantly in the solution. In real-world situations, deviations from ideal behaviour can occur, especially at high solute concentrations or when solute-solvent interactions are strong.
1. Boiling Point Elevation
Boiling point elevation refers to the increase in the boiling point of a solvent upon the addition of a solute. When a non-volatile solute is added to a solvent, the resulting solution has a higher boiling point than that of the pure solvent. For example, the boiling point of a solution of sodium chloride (salt) and water is greater than that of pure water.
- Boiling point elevation is a colligative property of matter, i.e. it is dependent on the solute-to-solvent ratio but not on the solute’s identity. This implies that the elevation in the boiling point of a solution depends on the amount of solute added to it.
- The greater the concentration of solute in the solution, the greater the boiling point elevation.

Why Does Boiling Point Elevation Occur?
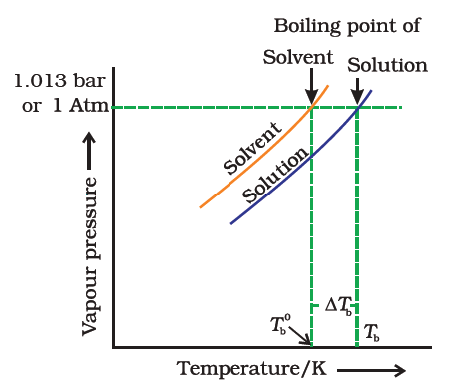
- Since the addition of a non-volatile solute causes a decrease in the vapour pressure of a solution, the boiling point of a solution is elevated as compared to the solvent i.e it must be heated to a higher temperature to make its vapour pressure equal to atmospheric pressure. Thus the solution boils at a higher temperature than the pure solvent.
- If Tb˚ is the boiling point of the solvent and Tb is the boiling point of the solution.
 Elevation in boiling point
Elevation in boiling point
We can see from the figure that the solution needs to be heated to a higher temperature to make it boil.
The difference between the boiling points of the solution and the solvent is known as the elevation in boiling point (ΔTb).
Elevation of boiling point, (ΔTb) = Boiling point of the solution - Boiling point of pure solvent
Elevation of boiling point, (ΔTb) = Tb -Tb˚
Experimentally, it is observed that elevation in boiling point is directly proportional to molal concentration of solute dissolved indefinite amount of the solvent.
ΔTb ∝ molality
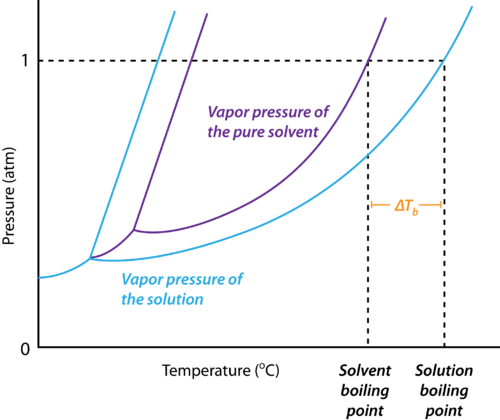
ΔTb = Kb × molality .....(1)
ΔTb = Kb × m
Where Kb is proportionality constant and is known as the molal boiling point elevation constant or the ebullioscopic constant. It has the units of degree kg mol-1 or K kg mol-1.
Molality can be written as:
Molality (m) = Number of moles of solute/Mass of solvent in kg
w = mass of solute in grams
M = molecular wt of solute
W = mass of solvent in gram.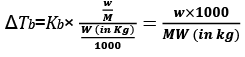
Significance of Kb
Now if, m = 1 then,
ΔTb = Kb. Thus, the molal elevation constant Kb is defined as the elevation of the boiling point when the molality of the solution is one i.e. when 1 mole of the solute is dissolved in 1 kg of the solvent, the elevation of boiling point is equal of Kb.
Example 1. A 5 percent aqueous solution by mass of a non-volatile solute boils at 100.15°C. Calculate the molar mass of the solute. Kb = 0.52 K kg mol -1.
Solution. The normal boiling point of water is 100°C.
The elevation in boiling point is 0.15°C.
A 5 percent solution means that in a 100 g solution 5 g of the solute is present.
This implies that the solvent is 95 g.
If the molar mass of the solute is M, then the molality of the solute in the solution is,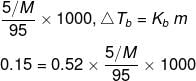
M = 182.4 g/mol
Example 2. A solution of 12.5 g urea in 170 g of water gave a boiling point elevation of 0.63 K. Calculate the molar mass of urea, taking Kb = 0.52 K/m.
Solution. Given: Mass of urea, w2 = 12.5 g
Mass of water, w1 = 170 g = 0.17 kg
Evaluation of boiling point, ΔTb = 0.63 K
Molar mass of urea, M = ?
Kb = 0.52 K m-1
Molar mass of the solute (urea) is given by: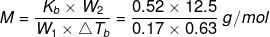
= 60.7 g mol-1
Example 3. Calculate the molecular mass of a substance 1.0 g of which on being dissolved in 100 g of solvent gave an elevation of 0.307 K in the boiling point. (Molal elevation constant (Kb) = 1.84 K/m).
Solution. We know that, ΔTb = , where n2 is the no. of moles of solute; w1 is the mass of the solvent in kg.
n2 = Mass of solute/Molar mass of the solute = 1.0 g/M and w1 = 100 g = 0.1 kg
Substituting these values, we get,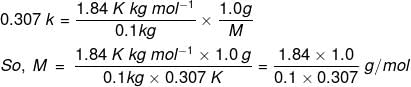
= 59.9 g/mol
TRY YOURSELF!
2. Freezing Point Depression
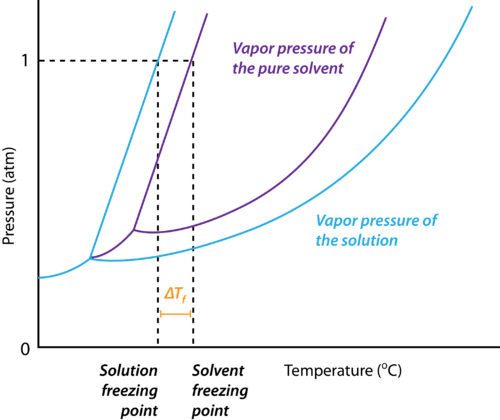
The freezing point of a substance is the temperature at which it's liquid and the solid phases have the same vapour pressure.
It is a colligative property of solutions that is generally proportional to the molality of the added solute. The depression in the freezing point of a solution can be described by the following formula: ΔTf = iKf × m
Where ΔTf is the freezing point depression,
i is the Van’t Hoff factor,
Kf is the cryoscopic constant, and
m is the molality.
 Depression in Freezing Point
Depression in Freezing Point
Why does the Freezing Point Depression Occur?
The reason for the depression of the freezing point of a solvent upon the addition of a solute is explained below:
- At the freezing point of a solvent, there exists an equilibrium between the liquid state and the solid-state of the solvent.
- This implies that the vapour pressures of both the liquid and the solid phase are equal.
- Upon the addition of a solute that is non-volatile, the vapour pressure of the solution is found to be lower than the vapour pressure of the pure solvent.
- This causes the solid and the solution to reach equilibrium at lower temperatures.
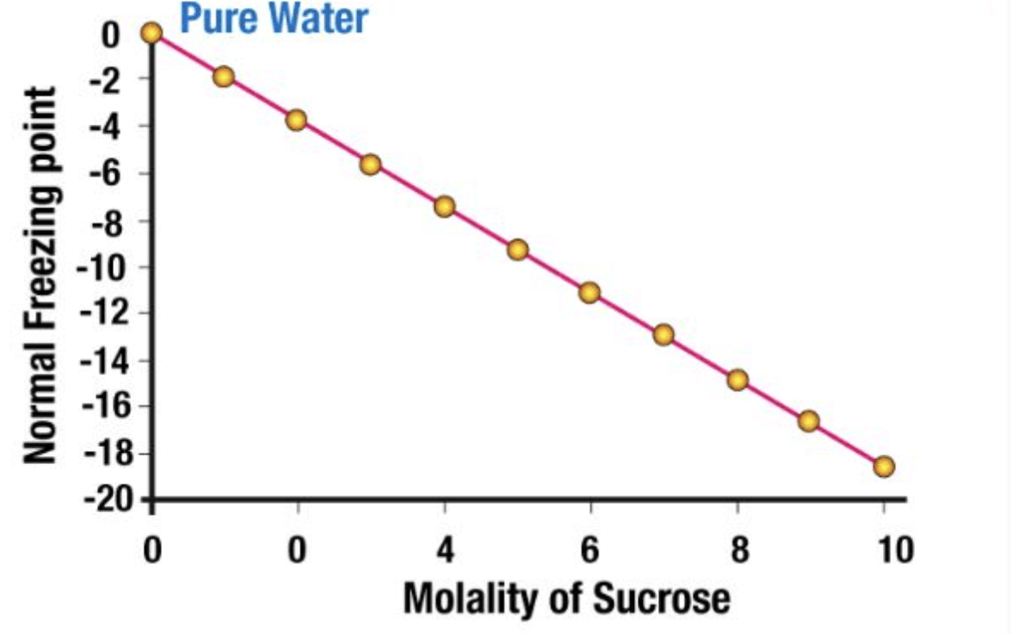
If the difference between the freezing point of the solvent and the solution is represented as ΔTf,
Depression of Freezing point, (ΔTf) = Freezing point of the solution - Freezing point of pure solvent
Depression of Freezing point, (ΔTf) = Tf -Tf˚
Experimentally, it is observed that Depression in the Freezing point is directly proportional to the molal concentration of solute dissolved indefinite amount of the solvent.
ΔTf ∝ molality
ΔTf = Kf × molality .....(1)
ΔTf = Kf × m
Where Kf is proportionality constant and is known as the molal Depression point constant or the Cryoscopic constant. It has the units of degree kg mol-1 or K kg mol-1.
Molality can be written as
Molality (m) = Number of moles of Solute/Mass of Solvent in Kg
w = mass of solute in grams
M = molecular wt of solute
W = mass of solvent in gram.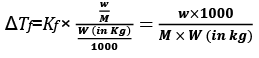
Significance of Kf:
ΔTf = Kfm. So, if m = 1 i.e. one mole of solute is dissolved in one kg of the solvent, then, ΔTf = Kf.
Thus,
The molal freezing point depression constant is equal to the depression in the freezing point produced when one mole of solute is dissolved in 1 kg of the solvent.
The values of molal elevation constant (Kb) for some common solvents are given in Table.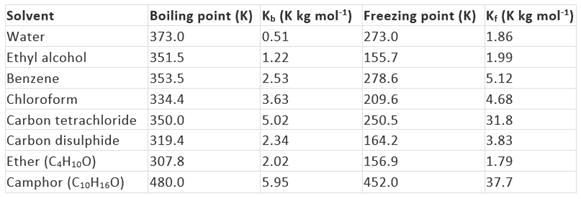
Kb and Kf can be obtained from the following relationships:
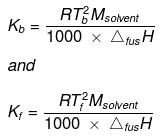
Where, Tb = boiling point of the solvent,
Tf = freezing point of the solvent,
Msolvent = molar mass of the solvent,
ΔvapH = enthalpy of vaporization and
ΔfusH = enthalpy of fusion.
Key concept: Camphor is commonly used in determining the molecular mass of a solute because of its very high cryoscopic constant (Kf).
Example 1. An aqueous solution of a non-volatile solute boils at 100.17°C. At what temperature would it freeze? (Kb = 0.52 K kg mol - 1 and Kf = 1.88 K kg mol - 1).
Solution.
ΔTb = 0.17°C
m = ΔTb/Kb = 0.17/0.52
= 0.327 molal,
ΔTf = Kf × molality
ΔTf = 1.86 × 0.327 = 0.608
Freezing point of the solution is - 0.608°C.
Example 2. 1.4 g of (acetone dissolved) in 100 g of benzene gave a solution which freezes at 277.12 K. Pure benzene freezes at 278.4 . 2.8 g of a solid (A) dissolved in 100 g of benzene gave a solution which froze at 277.76 K. Calculate the molecular weight of (A).
Solution.
For acetone solute + Benzene solvent mixture:
ΔT = K'f × 1000 × w/M × W
(278.40 − 277.12) = 1000 × Kf × 1.4/100 × 58
or 1.28 = 1000 × Kf × 1.4/100 × 58 ...(i)
For solute (A) + Benzene mixture (Let M be the molecular Weight of A)
(278.40 − 277.76) = 1000 × Kf × 2.8/100 × M ...(ii)
By Eqs. (i) and (ii)
M = 232g
Example 3. Ethylene glycol (HOH2C - CH2OH) is used as an antifreeze for water to be used in car radiators in cold places. How much ethylene glycol should be added to 1 kg of water to prevent it from freezing at -10°C? Molal depression constant of water is 1.86 K kg mol-1.
Solution.
Mass of water (solvent), w1 = 1 kg
ΔTf = 10°C Kf = 1.86 K kg mol-1
Mass of ethylene glycol required, w2 = ?
Molar mass of ethylene glycol = (12 + 3 +16) × 2 g/mol = 62 g/mol
We know, ΔTf = Kf(w2/62)/w1 or 10 = 1.86 × w2/62 x 1
This gives, w2 = 10 × 62 × 1/1.86 = 333.3 g
Example 4. Normal freezing point of a solvent is 150°C. A 0.5 molal solution of urea in the above solvent causes a freezing point depression of two degrees. Calculate the molal depression constant
Solution.
We know, ΔTf = Kfm
So, Kf = ΔTf/m = 2 deg/0.5 mol Kg-1 = 4 deg. kg mol-1
Example 5. A solution of urea in water freezes at 0.400°C. What will be the boiling point of the same solution if the depression and elevation constants for water are 1.86 deg kg mol-1 and 0.512 deg kg mol-1 respectively? Solution: We have the relationships:
Solution.
ΔTb = Kbn2/w1 ...(i)
And ΔTf = Kfn2/w1 ...(ii)
Where n2 is the number of moles of the solute, and w1 is the mass of solvent in kg.
Dividing equation (i) by equation (ii),
ΔTb/ΔTf = Kb/Kf
or,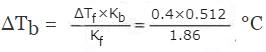
= 0.11°C
Then, Boiling point of the urea solution = 100°C + 0.11°C = 100.11°C.
TRY YOURSELF!
3.Relative Lowering of Vapour Pressure
The relative lowering of vapour pressure is one of the colligative properties in chemistry. On adding a nonvolatile solute to a solvent, the vapour pressure of the solution (solute + solvent) becomes lower than the vapour pressure above the pure solvent.
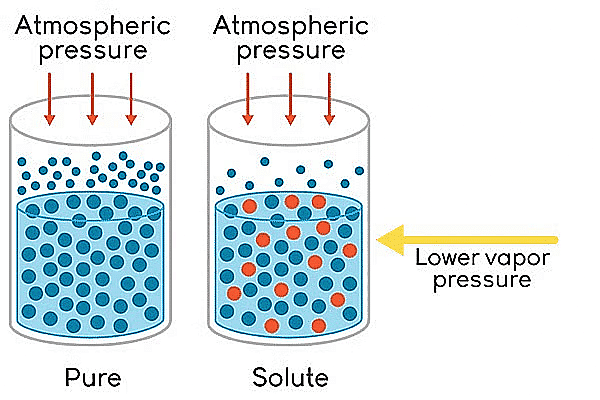 Lowering of Vapour Pressure
Lowering of Vapour Pressure
- The vapour pressure of a volatile solvent gets lowered when a non-volatile solute is dissolved in it.
- If p∘ represents then the vapour pressure of a pure solvent and p represents the vapour pressure of the solution, we have-
- Lowering of pressure: po - p
- Relative lowering of vapour pressure = po - p/ p
- The relative lowering of pressure and lowering of pressure are colligative properties.
- A relation between the pressure of the solution, the vapour pressure of the pure solvent, and the mole fraction of the solute were discovered by a French chemist Raoult.
- Raoult’s law, states that the lowering in vapour pressure of a dilute solution is equal to the mole fraction of the solute in the solution.

Here, n is the moles of the solute dissolved in N moles of the solvent.
Vapour Presure Lowering as a Colligative Property
Vapour pressure is not a colligative property. This is because vapour pressure does not depend on the number of solute particles but depends on the nature of the solute.
- Relative vapour pressure is a colligative property, i.e. it depends on the number of solute particles. The dissociation of ionic compounds will affect the vapour pressure of the solution. With an increase in the number of dissociated solute ions, the vapour pressure of the solution decreases.
- For example, it was found that the lowering of vapour pressure of a solution consisting of 1M NaCl is more than that of a solution having 1M glucose. The concentration of both solutions at standard temperature and pressure is the same. The reason behind this difference can be accounted for by the following reactions.
NaCl(s)→Na+(aq)+Cl–(aq) ⇒ 2 dissolved particles
C6H12O6(s)→C6H12O6(aq) ⇒1dissolved particles
Sodium chloride is an ionic compound that dissociates into two ions, whereas glucose being an organic compound does not dissociate. Therefore, equal concentrations of sodium chloride and glucose solution will result in twice as many dissolved particles in the case of sodium chloride. The vapour pressure of the sodium chloride solution will be lowered to twice the amount of the glucose solution.
[Question: 953761]
Relative Lowering of Vapour Pressure - Formula
Experimentally, we know that the vapour pressure of the solvent above a solution containing a nonvolatile solute (i.e., a solute that does not have a vapour pressure of its own) is directly proportional to the mole fraction of solvent in the solution. This behaviour is summed up in Raoult’s Law:
Psolution = Xsolvent × Posolvent
In a binary solution, if a volatile solute is added to the volatile solvent, each solute’s and solvent’s component is added to the total pressure
According to Raoult’s Law, the partial vapour pressure of two components, solvent (A) and solute (B), of a solution may be given as:
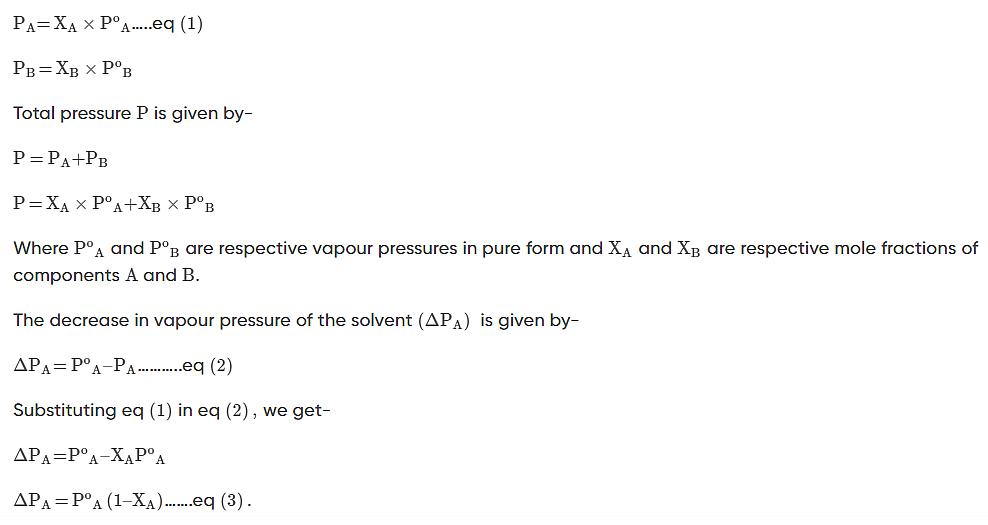

Vapour Pressure Lowering Example Problems With Solutions
Example 1: At 25oC the vapor pressure of pure benzene is 93.9 torr. When a nonvolatile solute is added to benzene, the vapour pressure of benzene is lowered to 91.5 torr. Calculate the mole fraction of the solute and the solvent.
Solution. 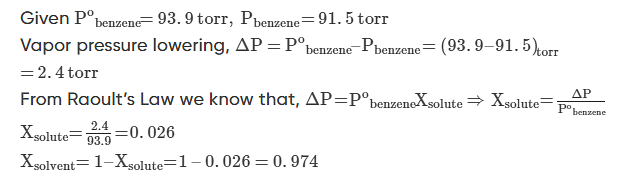
Example 2: The vapour pressure of a pure liquid at 298K is 4×104Nm2. On adding a nonvolatile solute, the vapour pressure of the solution becomes 3.65×104Nm2. Calculate the relative vapour pressure, lowering of vapour pressure, and relative lowering of vapour pressure.
Solution.

Example 3: The density of a 0.438 M solution of potassium chromate at 298 K is 1.063 g cm-3. Calculate the vapour pressure of water above this solution. Given: Po (water) = 23.79 mm Hg.
Solution.
A solution of 0.438 M means 0.438 mol of K2CrO4 is present in 1L of the solution. Now,
Mass of K2CrO4 dissolved per litre of the solution = 0.438 × 194 = 84.972 g
Mass of 1L of solution = 1000 × 1.063 = 1063 g
Amount of water in 1L of solution = 978.028/18 = 54.255 mol
Assuming K2CrO4 to be completely dissociated in the solution, we will have;
Amount of total solute species in the solution = 3 × 0.438 = 1.314 mol.
Mole fraction of water solution = 54.335/(54.335 + 1.314) = 0.976
Finally, Vapour pressure of water above solution = 0.976 × 23.79 = 23.22 mm Hg
Determination of Molar Masses from Lowering of Vapour Pressure
- It is possible to calculate molar masses of non-volatile non-electrolytic solutes by measuring the vapour pressures of their dilute solutions.
- Suppose, a given mass, w gram, of a solute of molar mass m, dissolved in
W gram of solvent of molar mass M lowers the vapour pressure from Po1 to P1. - We know that the relative lowering of the vapour pressure of a solution containing a non-volatile solute is equal to the mole fraction of the solute present in the solution.
- This implies

4. Osmosis and Osmotic Pressure
Osmosis is a fundamental biological and chemical process in which solvent molecules, typically water, move through a semipermeable membrane from a region of low solute concentration to a region of high solute concentration. This movement aims to balance the concentrations on either side of the membrane.
Semipermeable Membranes (SPM) are critical components in processes like osmosis. They selectively allow certain molecules to pass through while blocking others based on size or other properties. In the context of solutions, they typically allow the solvent (e.g., water) to pass through but prevent the solute (e.g., salt) from crossing. This selective permeability is due to the presence of tiny pores in the membrane.
Key Characteristics of Semipermeable Membranes:
(i) Selective Permeability
- Solvent Passage: The pores are small enough to let solvent molecules pass through.
- Solute Exclusion: Larger solute molecules are blocked due to their size.
(ii) Material and Structure
- Made of materials like cellulose acetate, polyamide, or other polymers.
- The structure consists of a network of submicroscopic pores that act as a sieve.
(iii) Applications
- Biological Systems: Cell membranes, which regulate the passage of nutrients and waste.
- Industrial Uses: Water purification, dialysis, and other filtration processes.
Osmotic Pressure (π)
Osmotic Pressure is a fundamental concept in the study of solutions and osmosis. It refers to the pressure required to prevent the flow of a solvent through a semipermeable membrane into a solution containing a higher concentration of solute.
Role in Osmosis:
When two solutions of different concentrations are separated by an SPM, solvent molecules naturally move from the area of lower solute concentration to the area of higher solute concentration. Osmotic pressure is the force that balances this movement, preventing further solvent flow when equilibrium is reached.
Van't Hoff Laws of Osmotic Pressure
Van't Hoff-Boyle's Law:
- Statement: The osmotic pressure (π) of a solution is directly proportional to its molar concentration (C), when the temperature is kept constant.
- Mathematical Representation: π∝C
- This means that if the concentration of solute in a solution increases, the osmotic pressure also increases, assuming the temperature does not change.
Van't Hoff-Charles' Law:
- Statement: At constant concentration, the osmotic pressure of a dilute solution is directly proportional to its absolute temperature (T).
- Mathematical Representation: π∝T
- This implies that if the temperature of a solution rises, the osmotic pressure will also rise, given that the concentration remains the same.
Combined Van't Hoff Law:
- By combining the above two laws, the osmotic pressure is given by: π∝C⋅T Or, more precisely: π=CRT
- Where:
- π is the osmotic pressure.
- C is the molar concentration of the solution.
- R is the universal gas constant.
- T is the absolute temperature in Kelvin.
Isotonic or Iso-Osmotic Solutions
- Definition: Solutions that have the same osmotic pressure at a given temperature are called isotonic or iso-osmotic solutions.
- Behavior: When isotonic solutions are separated by a semipermeable membrane, no net osmosis occurs between them. This means that there will be no movement of water across the membrane since the osmotic pressures are balanced.
Example: Osmotic Pressure in Biological Systems
Normal Saline Solution: The fluid inside a blood cell has an osmotic pressure equivalent to that of a 0.9% (mass/volume) sodium chloride solution, also known as normal saline. This concentration is isotonic to the blood cells, meaning it is safe for intravenous injections as it does not cause the cells to shrink or swell.
Hypertonic Solution: A solution with a higher concentration of solutes (e.g., more than 0.9% sodium chloride) is hypertonic relative to the inside of the blood cells. If blood cells are placed in such a solution, water will flow out of the cells, causing them to shrink (crenation).
Hypotonic Solution: A solution with a lower concentration of solutes (e.g., less than 0.9% sodium chloride) is hypotonic relative to the inside of the blood cells. Placing blood cells in this solution will cause water to flow into the cells, leading them to swell and potentially burst (lysis).
Some Important Questions
Q.1. What are the properties arising due to varying concentrations of solute in a given solvent, irrespective of the nature of the solute concerning the solvent?
a) Colligative properties
b) Intensive properties
c) Extensive properties
d) Solute properties
Ans: a
Colligative properties are a set of four properties. This set of properties purely depends on the number of solute particles present in the solution/solvent, independent of the nature of the particles concerning the solution/solvent.
The properties are
1.) Relative lowering of vapor pressure,
2.) Elevation in boiling point,
3.) Depression in freezing point and
4.) Osmotic pressure.
Q.2. Which law specifically governs the relative lowering of vapor pressures in solutions?
a) Van’t Hoff law
b) Boyle’s law
c) Raoult’s law
d) Amagat’s law
Ans: c
Raoult’s law quantifies the relative lowering in vapor pressure. From the law, it follows that p1 = X1 x po1. If p01 was the original pressure before the X2 mole fraction of solute was added to the solvent then a reduction in vapor pressure is given as:
Δp1 = po1 – p
= po1 – po1 X1
= po1(1 – X1)
= po1X2
Therefore, the relative reduction in vapor pressure (∆p1/po1) = X2 i.e. mole fraction of solute in the solution.
Q.3. On addition of non-volatile potassium iodide in water at 298K it is noticed that vapor pressure reduces from 23.8 mm Hg to 2.0 cm Hg. What is the mole fraction of solute in the solution?
a) 0.916
b) 0.160
c) 0.084
d) 0.092
Ans: b
Given,
P0water =23.8 mm Hg
Pwater= 2.0 cm Hg = 20.0 mm Hg (after addition of solute)
From the law of relative lowering of vapor pressure, ∆p1 = X2 x po1 (where X2 is the mole fraction of solute)
On rearranging, Δp1/po1 =X2
Δp1 = 23.8 – 20.0 = 3.8 mm Hg
X2 = 3.8/23.8 = 0.160
Q.4. Which of the following is Raoult’s law applicable to, to determine molar masses correctly?
a) Ionic solute in liquid
b) Non-ionic solute in dilute solution
c) Non-ionic solute in concentrated solution
d) Ionic solid in insoluble form in solvent
Ans: b
To determine molar masses correctly, the solute must be non-volatile, non-ionic, and present in dilute form only. If it is ionic one has to account for its van’t Hoff factor, i, for association in concentrated solution and dissociation in dilute solution. Molar masses can only be calculated from dilute solutions containing non-dissociable non-ionic solutes.
Q.5. Which of the following is a colligative property?
a) Relative lowering of fluid pressure
b) Decrease in boiling point
c) Decrease in freezing point
d) Change in volume after mixing
Ans: c
A decrease in freezing point is the correct colligative property, known as ‘Depression in freezing point’. This is caused by solute particles present on the surface which lowers the equilibrium solid-vapor pressure. Therefore, a lower freezing temperature is required to match the pressure outside. The other correct colligative properties are
1.) Relative lowering of vapor pressure,
2.) Elevation in boiling point,
3.) Depression in freezing point and
4.) Osmotic pressure.
Q.6. Mass of Urea (NH2CONH2) required to be dissolved in 1000 g of water in order to reduce the vapour pressure of water by 25% is _________ g. (Nearest integer)
Given: Molar mass of N, C, O and H are 14,12,16 and 1 g mol−1 respectively
Ans: 1111
Given: Vapor pressure reduction: 25% (0.75 times the vapor pressure of pure water)
Molar mass of water (H2O): 18g/mol
Mass of solvent (water): 1000g
Using Raoult's law:
Solving for (x):
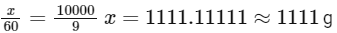
So, the mass of urea required to be dissolved in 1000g of water is 1111g.
|
108 videos|286 docs|123 tests
|
FAQs on Colligative Properties: Elevation in B.P., Depression in F.P., Relative Lowering in Vapour Pressure - Chemistry Class 12 - NEET
| 1. What is the relationship between colligative properties and the number of solute particles in a solution? |  |
| 2. How does boiling point elevation affect the boiling point of a solvent in a solution with a non-volatile solute? |  |
| 3. Why does adding a solute to a solvent result in freezing point depression? |  |
| 4. How does relative lowering of vapor pressure relate to the presence of solute particles in a solution? |  |
| 5. What is the significance of osmosis and osmotic pressure in relation to colligative properties? |  |

|
Explore Courses for NEET exam
|

|