Collision Theory & Variations in Arrhenius Equation | Physical Chemistry for NEET PDF Download
| Table of contents |

|
| Collision Theory of Chemical Reaction |

|
| Mechanism of Reaction |

|
| Arrhenius Equation |

|
| Variation in Arrhenius equation |

|
Collision Theory of Chemical Reaction
- Though the Arrhenius equation is applicable under a wide range of circumstances, collision theory, which was developed by Max Trautz and William Lewis in 1916 -18, provides greater insight into the energetic and mechanistic aspects of reactions. It is based on the kinetic theory of gases.
- According to this theory, the reactant molecules are assumed to be hard spheres and reaction is postulated to occur when molecules collide with each other.
- The number of collisions per second per unit volume of the reaction mixture is known as collision frequency (Z). Another factor that affects the rate of chemical reactions is activation energy (as we have already studied). For a bimolecular elementary reaction.
A + B → Products rate of reaction can be expressed as
Rate = ..............(1)
where represents the collision frequency of reactants, A and B and
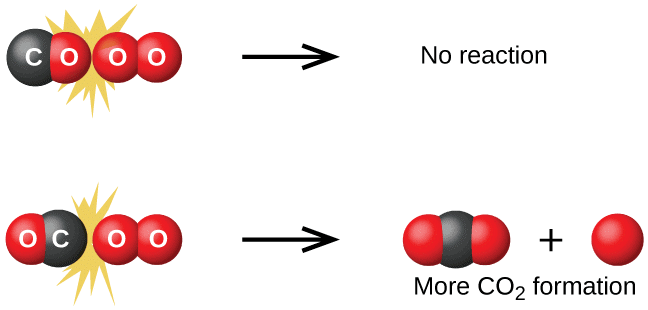
represents the fraction of molecules with energies equal to or greater than Ea. Comparing (1) with Arrhenius equation, we can say that A is related to collision frequency. Equation (1) predicts the value of rate constants fairly accurately for the reactions that involve atomic species or simple molecules but for complex molecules significant deviations are observed. The reason could be that all collisions do not lead to the formation of products. The collisions in which molecules collide with sufficient kinetic energy (called threshold energy*) and proper orientation, so as to facilitate breaking of bonds between reacting species and formation of new bonds to form products are called as effective collisions.
To account for effective collisions, another factor P, called the probability or steric factor is introduced. It takes into account the fact that in a collision, molecules must be properly oriented i.e.,
Rate =
Thus, in collision theory activation energy and proper orientation of the molecules together determine the criteria for an effective collision and hence the rate of a chemical reaction.
Mechanism of Reaction
Reactions can be divided into
Elementary/Simple/single step
Complex/multi-step
Elementary Reaction
These reaction take place in single step without formation of any intermediate
For elementary reaction we can define molecularity of the reaction which is equal to no of molecules which make transition state or activated complex because of collisions in proper orientation and with sufficient energy
molecularity will always be a natural no
1 = unimolecular one molecular gets excited (like radioactivity)
2 = bimolecular
3 = trimolecular
Molecularity < 3 because the probability of simultaneous collision between 4 or mor molecules in proper orientation is very low
For elementary reaction there is only single step and hence it is going to be rate determining step so order of an elementary reaction is its molecularity
Order of elementary reaction w.r.t reactant = stoichiometric co-efficient of the reactant
rate = k [H2] [I2]
(no elementary)
reaction obtained by multiplying and elementary reaction with some no will not be of elementary nature
order = 0
Complex Reaction
Reaction which proceed in more than two steps or having some mechanism. (sequence of elementary reaction in which any complex reaction proceeds)
For complex reaction each step of mechanism will be having its own molecularity but molecularity of net complex reaction will not be defined.
Order of complex reaction can be zero fractions whole no, even negative w.r.t some species.
Order of reaction or rate law of reaction is calculated with the help of mechanism of the reaction generally using rate determine step (R.D.S) if given.
Rate law of a reaction is always written in terms of conc. of reactant, products or catalysts but never in terms of conc. of intermediates.
The mechanism of any complex reaction is always written in terms of elementary steps, so molecularity of each of these steps will be defined but net molecularity of complex reaction has no meaning.
The mechanism of most of the reaction will be calculated or predicted by using mainly the following approximation.
The Rate-Determining-Step Approximation %
In the rate-determining-step approximation (also called the rate-limiting-step approximation or the equilibrium approximation), the reaction mechanism is assumed to consist of one or more reversible reactions step, which in turn is followed by one or more rapid reactions. In special cases, there may be no equilibrium steps before the rate-determining step or no rapid reactions after the rate-determining step.
When steps 2 B (C) is assumed to be the rate-determining step. For this assumption to be valid, we must have k-1 >> k2. The slow of
compared with
ensures that most B molecules go back to A rather than going to C, thereby ensuring that step
remains close to equilibrium. Further-more, we must have k3 >> k2 and k3 >> k-2 to ensure that step 2 acts as a"bottleneck" and that product D is rapidly formed from C. The overall rate is then controlled by the rate-determining step
. (Note that since k3 >> k-2, the rate-limiting step is not in equilibrium.) Since we are examining the rate of the forward reaction
, we further assume that k2[B] >> k-2[C]. During the early stage of the reaction, the concentration of C will be low compared with B, and this condition will hold. Thus we neglect the reverse reaction for step 2. Since the rate-controlling step is taken to be essentially irreversible, it is irrelevant whether the rapid steps after the rate-limiting step are reversible or not. The observed rate law will, depends only on the nature of the equilibrium that precede the rate-determining step and on this step itself.
Arrhenius Equation
Number of effective collisions = Number of collision x fraction.
F k = A e-Ea/RT
Where , k = rate constant of reaction
A = Pre exponential factor or Arrhenius constant or Frequency factor.
Ea = Activation energy
R = Universal gas constant
T = Absolute temperature.
⇒ Fraction of molecules undergoing effective collision
Variation in Arrhenius equation
Type -1 :
log k = 2 - ; A = ? Ea = ?
k = Ae-Ea/RT
loge k = loge A -
log k = log A -
log10 A = 2 A = 102 = 100
Ea = 2.303 x R x 5 x 10-3
Type -2 : Temperature Variation :
r1 K1
T1
r2 K2
T2
log k1 = log A - , log k2 = log A -
Type -3 : Addition of Catalyst :
r1 k1
no catalyst
Ea
T
r2 k1
catalyst
Eac
T
log k1 = log A -
log k2 = log A -
log
Type -4 : Both Catalyst and Temperature :
Q. At 278 oC the half life period for the first order thermal decomposition of ethylene oxide is 363 min and the energy of activation of the reaction is 52,00 cal/mole. From these data estimate the time required for ethylene oxide to be 75% decomposed at 450�C.
Sol. ln =
=
t1/2 (at 450oC) = 118.24 min.
Now
Therefore, t0.75 = x 118.24 = 236.48 min
Q. The activation energy of the reaction : A + B → products is 102.9 kJ/mol. At 40oC, the products are formed at the rate of 0.133 mol/L/min. What will be rate of formation of products at 80oC?
Sol. Let the rate law be defined as
At T1 : r1 = k1[A]x[B]y
At T2 : r2 = k2[A]x [B]y
⇒ r2 = r1
Using Arrhenius equation find k at 40oC.
log10 =
⇒
⇒ log10 = 1.95 ⇒
⇒ r2 = 0.133 x 88.41 = 11.76 mol/L/min
Q. The activation energy of a non-catalysed reaction at 37oC is 200 kcal/mol and the activation energy of the same reaction when catalysed decreases to only 6.0 kcal/mol. Calculate the ratio of rate constants of the two reactions.
Sol. We know that :
Let k = rate constant for non-catalysed reaction and kc rate constant for catalysed reaction. Let Ea be the activation energy for non-catalysed reaction and Eac be the energy of activation of catalysed reaction.
1.
2.
⇒ ⇒
⇒
⇒ ⇒
or
Q. A first order reaction A → B requires activation energy of 70 kJ/mol. When 20% solution of A was kept at 25oC for 20 minutes, 25% decomposition took place. What will be the percent decomposition in the same time in a 30% solution maintained at 40oC? Assume that the activation energy remains constant in this range of temperature.
Sol. Note : It does not matter whether you take 20%, 30%, 40% or 70% of A.
At 25oC, 20% of A decomposes 25%
⇒ kt = 2.303 log10
⇒ k(40) = 2.303 log10 ⇒ k(at 25oC) = 0.0143 min-1
Using Arrhenius equation find k at 40oC.
⇒ k(at 40oC) = 0.055 min-1
Now calculate % decomposition at 40oC using first order kinetics.
kt = 2.303 log10
⇒ 0.055 x 40 = 2.303 log10
⇒ x = 67.1 ≡ 67.1% decomposition of A at 40oC.
Q. The rate constant of a reaction is 1.5 x 107 sec-1 at 50oC and 4.5 x 107 sec-1 at 100oC. Evaluate the Arrhenius parameters A and Ea.
Sol. Therefore, 2.303 log10 =
Therefore, 2.303 log10 =
Therefore, Ea = 2.2 x 104 J mol-1
Now, Therefore, 4.5 x 107 =
Therefore, A = 5.42 x 1010
Q. A reaction proceeds five times more at 60oC as it does at 30oC. Estimate energy of activation.
Sol. Given, T2 = 60 + 273 = 333 K, T1 = 30 + 273 = 303 K,
R = 1.987 x 10-3 kcal
r = k [ ]n (at a temperature T)
Therefore, (at temp. T2 and T1)
Therefore,
2.303 log10
Therefore, 2.303 log10 5 =
Ea = 10.757 kcal mol-1
Q. The rate constant of a reaction increases by 7% when its temperature is raised from 300 K to 310 K, while its equilibrium constant increases by 3%. Calculate the activation energy of the forward and reverse reactions.
Sol. Rate constant at 300K = k
Therefore, Rate constant at 310 K = k + = 1.07 k
Thus, 2.303 log
2.303 log
Therefore, = 1258.68 cal
Now, equilibrium constant at 300 K = K'
Equilibrium constant at 310 K = K' + 3/100 x K' = 1.03 K'
Using 2.303 log =
2.303 log
Therefore, ΔH = 549.89 cal
Since, ΔH =
Therefore, 549.89 = 1258.68 -
Therefore, = 708.79 cal
Q. At 380oC, the half life period for the first order decomposition of H2O2 is 360 min. The energy of activation of the reaction is 200 kJ mol-1. Calculate the time required for 75% decomposition at 450oC. [IIT 1995]
Sol. K1 = 0.693/360 min-1 at 653 K and
Ea = 200 x 103 J, K2 = ? at 723 K, R = 8.314 J
Therefore, From 2.303 log10 (K2 / K1) = (Ea/R)[(T2 - T1)/(T1T2)]
K2 = 0.068 min-1
Now, t = log10
= 20.39 minute
|
117 videos|226 docs|237 tests
|
FAQs on Collision Theory & Variations in Arrhenius Equation - Physical Chemistry for NEET
| 1. What is the collision theory of chemical reactions? |  |
| 2. How does the mechanism of a reaction relate to the collision theory? |  |
| 3. What is the Arrhenius equation and how does it relate to the collision theory? |  |
| 4. What are the variations in the Arrhenius equation? |  |
| 5. How do variations in the Arrhenius equation affect the rate of a reaction? |  |















