Completing the Square | Mathematics for GCSE/IGCSE - Year 11 PDF Download

Completing the Square

How can I rewrite the first two terms of a quadratic expression as the difference of two squares?

• Consider the quadratic expression x² + bx + c. 
• The first two terms can be expressed as the difference of two squares using the following principle: x² + bx is equivalent to (x + p)² − p², where p is half of b.
• To verify this, expand the right-hand side. 
  • Is x² + 2x equivalent to (x + 1)² − 1²? 
    • Yes, as (x + 1) − 1² = x² + 2x + 1 − 1 = x² + 2x. 
• This holds true for negative values of b as well. 
  • For instance, x² − 20x can be expressed as (x − 10)² − (−10)², which simplifies to (x − 10)² − 100. Notably, a negative b does not change the sign at the end.

How do I complete the square?

• Completing the square is a way to rewrite a quadratic expression in a form containing a squared-bracket
• To complete the square on x² + 10x + 9
  • Use the rule above to replace the first two terms, x² + 10x, with (x + 5)² - 5²
  • then add 9:  (x + 5)² - 5² + 9
  • simplify the numbers:  (x + 5)² - 25 + 9
  • answer: (x + 5)² - 16 

How do I complete the square when there is a coefficient in front of the x2 term?

• You first need to take a out as a factor of the x² and x terms only
• 
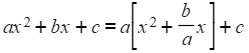
  • Use square-shaped brackets here to avoid confusion with curly brackets later
• Then complete the square on the bit inside the square-brackets:
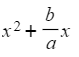
  • This gives
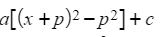
  • where p is half of b/a
• Finally multiply this expression by the a outside the square-brackets and add the c
  • 
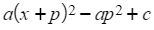
  • This looks far more complicated than it is in practice!
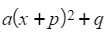
    • Usually you are asked to give your final answer in the form
• For quadratics like -x² + bx + c, do the above with a = -1

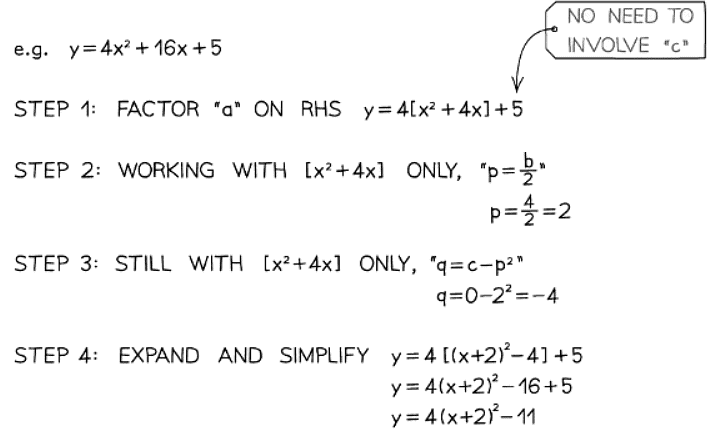
How do I find the turning point by completing the square?

• Completing the square aids in locating the turning point on a quadratic graph. 
  • When the equation is y = (x + p) ² + q, the turning point is situated at (−p, q), noting the negative sign in the x-coordinate. 
  • This concept connects to graph transformations, where y = x ² is shifted by p to the left and q upwards.
  • Even with a coefficient, if y = a(x + p) ² + q, the turning point remains at (−p, q). 
  • If a > 0, the turning point is at a minimum, while if a < 0, it is at a maximum. 
• Additionally, completing the square assists in formulating the equation of a quadratic when the turning point is given.

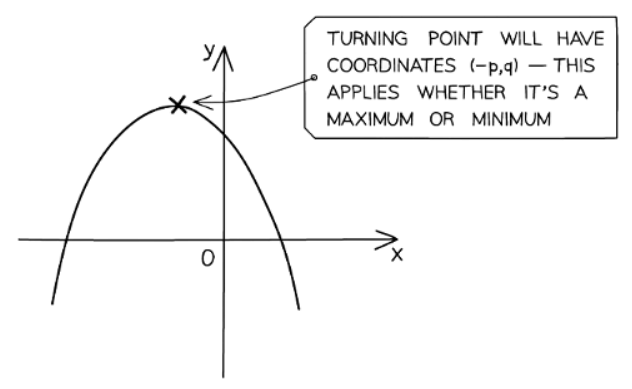
• It can also be used to prove and/or show results using the fact that any "squared term", i.e. the bracket (x ± p)2, will always be greater than or equal to 0
  • You cannot square a number and get a negative value

Solving by Completing the Square

How do I solve a quadratic equation by completing the square?

• To solve x² + bx + c = 0 
  • replace the first two terms, x² + bx, with (x + p)² - p² where p is half of b
  • this is called completing the square
    • x² + bx + c = 0 becomes
      • (x + p)² - p² + c = 0 where p is half of b
  • rearrange this equation to make x the subject (using ±√)
• For example, solve x² + 10x + 9 = 0 by completing the square
  • x² + 10x becomes (x + 5)² - 5²
  • so x² + 10x + 9 = 0 becomes (x + 5)² - 5² + 9 = 0
  • make x the subject (using ±√)
    • (x + 5)² - 25 + 9 = 0
    • (x + 5)² = 16
    • x + 5 = ±√16
    • x  = ±4 - 5
    • x  = -1 or x  = -9
• If the equation is ax² + bx + c = 0 with a number in front of x², then divide both sides by a first, before completing the square

How does completing the square link to the quadratic formula?

• The quadratic formula actually comes from completing the square to solve ax² + bx + c = 0
  • a, b and c are left as letters, to be as general as possible
• You can see hints of this when you solve quadratics 
  • For example, solving x² + 10x + 9 = 0 
    • by completing the square, (x + 5)² = 16 so x  = ± 4 - 5 (from above)
    • by the quadratic formula, 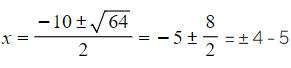(the same structure)