Concepts of Value and Return - 1 | Management Optional Notes for UPSC PDF Download
Introduction
- You've likely heard the saying that a rupee today holds more value than a rupee tomorrow. But have you ever wondered why? Let's consider an example: Sriram's grandfather offers him a gift of Rs. One lakh at the end of the fifth year or Rs. 75,000 today. If you were in Sriram's shoes, which option would you choose?
- Would you accept Rs. 1,00,000 after five years or Rs. 75,000 today? The immediate Rs. 75,000 might seem more appealing than the Rs. 1,00,000 in the future because the present holds more certainty than the distant future. By investing Rs. 75,000 now, you could potentially earn a return on that amount. Furthermore, Rs. 1,00,000 received after five years may have less purchasing power due to inflation.
- Hopefully, you now understand the principle that a rupee today holds greater value than a rupee tomorrow. However, matters related to money are rarely straightforward. The concept of the time value of money sheds light on the intricacies of such choices we encounter in our daily lives.
- In our routine activities, many investment decisions involve cash flows occurring at different points in time. Therefore, understanding the concept of the time value of money is crucial.
Future Value
- Future value (FV) represents the anticipated worth of a current asset at a specified future date, based on an assumed growth rate. This metric holds significance for investors and financial planners, serving as a tool to estimate the potential value of an investment made today. Understanding the future value empowers investors to make informed decisions aligned with their future financial needs.
- However, external economic factors, such as inflation, can exert a negative influence on the future value of an asset, diminishing its purchasing power over time.
- Determining the FV of an asset can be complex and varies depending on the type of asset involved. Additionally, the calculation of FV relies on the assumption of a consistent growth rate. When funds are placed in a savings account with a fixed interest rate, accurately determining the future value becomes more straightforward.
- To grasp the fundamental concept, simple and compound interest rates serve as clear examples of FV calculations. In essence, future value represents the growth of an initial investment over time, at a specified interest rate.
Future Value Calculation
Future value calculations can be categorized into two types:
Future Value of a Lump Sum:
- This calculation pertains to the value of a single deposit, such as a bank fixed deposit, over a period of time.
Future Value of an Annuity:
- This calculation concerns the value of a series of payments made at regular intervals, like insurance premium payments, over time. An annuity involves a sequence of payments of uniform amounts.
Utilizing one of the numerous free online calculators or financial calculator applications, such as the HP 12C Financial Calculator, accessible on platforms like Google Play and the Apple App Store, is the simplest method to compute future value. Most spreadsheet programs also offer functions for future value calculations. However, for this course's purposes, we will reference present value, future value, and annuity tables provided within the course materials. The future value (FV) formula assumes a consistent rate of growth and a single initial payment that remains untouched throughout the investment period. The FV calculation can be approached in one of two ways, depending on the type of interest earned:
i) Using Simple Annual Interest:
If an investment earns simple interest, the FV formula is:
If an investment earns simple interest, then the FV formula is:
FV = P × (1 + R × T)
Where,
FV= Future Value
P = Principal amount or Investment Amount
R = Interest rate
T = Number of years
FV= Future value or final amount
For example, assume a Rs.1,000 investment is held for five years in a savings account with 10% simple interest paid annually.
In this case, the FV of the Rs.1,000 initial investment is Rs1,000 × [1 +
(0.10 x 5)], or Rs.1,500.
(ii) Compounded Annual Interest
In contrast to simple interest, which applies the interest rate solely to the initial investment, compounded interest applies the rate to the cumulative balance of each period. In the given example, during the first year of investment, an interest of 10% × Rs.1,000, or Rs.100, is earned. However, in the subsequent year, the account balance stands at Rs.1,100 instead of Rs.1,000. Consequently, to compute compounded interest, the 10% interest rate is applied to the entire balance, resulting in second-year interest earnings of 10% × Rs.1,100, or Rs.110.
The formula for determining the Future Value (FV) of an investment earning compounded interest is:
FV = P × (1 + R)t
Where,
P = Principal amount or Investment amount
R = Interest rate
t = Number of years
Using the above example, the same Rs.1,000 invested for five years in a savings account with a 10% compounding interest rate would have an FV of Rs.1,000 × [(1 + 0.10)5], or Rs.1,610.51.
Future Value of an Annuity Example
A common use of future value is planning for a financial goal, such as funding a retirement savings plan. Future value is used to calculate what you need to save and invest each year at a given rate of interest to achieve that goal.
In general terms the future value of an Annuity is given has the following formula:
FV An = A[(1 + r)n − 1]/r
Where,
Fv An= Future Value of annuity
A = constant Periodic flows
r= Interest rate period
n= duration of annuity
Example 1
If you contribute Rs. 2,400 every year to a retirement account and want to calculate what that account will be worth in 30 years; you could use the future value of an annuity formula. For this example, you assume a 7% annual rate of return: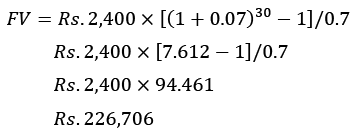
Over 30 years, you would contribute a total of Rs. 72,000, but because of the time value of money and the power of compounding interest, your account would be worth Rs. 226,706 (with an annual 7% rate of return), or more than three times the amount you invested.
Future value is also useful to decide the mix of stocks, bonds, and other investments in your portfolio. The higher the rate of interest, or return, the less money you need to invest to reach a financial goal. Higher returns, however, usually mean a higher risk of losing money.
The term [(1 + r)n — 1]/r is referred to as the future value interest factor for an annuity(FVIFAr.n) and the value of this factor for several combinations of r and n can be found in the annuity table.
Present Value Vs. Future Value
- Another significant concept in finance is the present value of money, which pertains to the value of future cash flows when assessed in today's terms. By utilizing present value, you can ascertain the current worth of an asset or sum of money based on its future value. This process is often termed "discounting" because, due to any positive rate of return, the present value is typically lower than its future equivalent.
- The interest rate employed to compute the present value of anticipated future cash flows is known as the "discount rate." To illustrate present value, consider the following example: Suppose Rs. 1,000 is deposited into an account with an annual interest rate of 2% for one year. The future value of this deposit would be Rs. 1,020, calculated as FV = 1000 × (1 + .02)1 = Rs. 1,020. Conversely, we can infer that the present value of Rs. 1,020 is Rs. 1,000, as it represents the initial amount invested. Essentially, present value serves as the counterpart to future value.
- The relationship between Present Value and Future Value
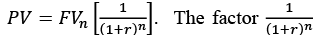 is called the discounting factor or the present value interest factor (PVIFr,n).
is called the discounting factor or the present value interest factor (PVIFr,n).
Some common uses for present value include:
- Calculating the value of pension annuity payments versus taking a lump sum
- Determining whether a business owner’s investment will meet profit expectations.
- Valuing a business
Time Value of Money and Its Significance
Understanding the concept of the time value of money is crucial for financial planning, influencing decisions ranging from asset acquisition to investment strategies. The future value reflects how time affects the worth of money, and leveraging future value alongside other metrics can facilitate informed financial choices.
From a financial management perspective, the significance of the time value of money becomes evident in several ways:
- Capital Structure Management: Companies aiming for expansion and growth utilize a blend of internal funds (equity and retained earnings) and external funds (debt). Appreciating the time value of money aids in assessing the impact of debt on a company's earnings and profitability.
- Risk Management and Profit Generation: Given the uncertainty of the future, understanding the time value of money is crucial for effective fund management and profit generation within a corporation.
- The time value of money plays a pivotal role in financial decision-making. For instance, consider an investor evaluating two projects: Project ‘A’ and Project ‘B’. While both projects offer a Rs. 1 million cash reward, Project ‘A’ promises it in year one, whereas Project ‘B’ offers it in year five. Without grasping the time value of money, both projects may seem equally appealing. However, in reality, due to Project ‘A’ having a higher present value than Project ‘B,’ understanding the time value of money dictates that Project ‘A’ is the more attractive option.
Calculation of Time Value of Money
The Time Value of Money can be calculated in two ways. The following formula can be used to calculate the present value (PV) of future cash flows:
PV = FV X (1 + r)-n or FV= PV x (1+r)n
Where:
PV — Present Value.
FV — Future Value.
r — interest rate.
n — number of periods.
Notice the negative sign of the power n which allows us to remove the fractions from the equation.The following formula allows us to calculate the future value FV) of cash flow from its present value.
FV = PV X (1 + r)n
Where:
FV — Future Value.
PV — Present Value.
r — interest rate.
n — number of periods.
Effect of Compounding Periods on Future Value
The number of compounding periods used in time value of money estimates can have a significant impact. If the number of compounding periods is raised to quarterly, monthly, or daily in the Rs. 10,000 example above, the concluding future value calculations are:
- Quarterly Compounding: FV = Rs. 10,0000 X [1 + (10%/4)]4x1 = Rs. 11,038
- Monthly Compounding: FV = Rs. 10,0000 X [1 + (10%/12)]12x1 = Rs. 11,047
- Daily Compounding: FV = Rs. 10,0000 X [1 + (10%/365)]365x1 = Rs. 11,052
This demonstrates that the time value of money is determined not just by the interest rate and time horizon, but also by the number of times the compounding computations are performed each year.
In cases where we have more than one compounding period of interest per year, we can tweak the formula, to make sure we are using the appropriate portion of annual interest:
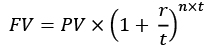
Where:
FV — Future Value.
PV — Present Value.
r — interest rate (annual).
n — number of periods (years).
t — number of compounding periods of interest per year. If it is quarterly t=4, for half-yearly t=2, and for monthly t=12.
The time value of money is a fundamental concept in determining Net Present Value (NPV), Compound Annual Growth Rate (CAGR), Internal Rate of Return (IRR), and other financial calculations.
- The general formulas of this concept can be applied to any series of cash flows. Financial calculators or spreadsheet programs like Excel can be used to calculate the metrics related to the time value of money. You can find specific business functions or look for the following ones in Excel: PV, FV, IRR, NPV.
- Selecting the appropriate rate of return is crucial in time value of money assessments (discount rate). Besides interest on debt, the Weighted Average Cost of Capital (WACC) is a common rate option. It's essential to understand that making the wrong rate decision can render the entire process meaningless and severely impact decision-making.
In practice, there are two types of time value of money concepts described below:
(i) Time Value of Money for a One-Time Payment
- For example, investing INR 10,000 for 5 years in a bank offering a 10% annual interest rate and allowing it to grow cumulatively. After 5 years, the accumulated total value would be Rs. 16,110. Whether Rs. 10,000 is worth more than Rs. 16,110 depends on factors like the inflation rate, interest rate, and risk involved. It's a loss if the inflation rate rises, and a gain if the interest rate falls.
(ii) Time Value of Money - Doubling the Period
- Another scenario involves calculating when the amount of money will double. The rule of 72 can estimate the doubling period by dividing 72 by the interest rate. For instance, if you invest Rs. 10,000 for 5 years at an 8% interest rate, it will take 9 years to double the present value of your money.
Example 1: Assuming a sum of Rs. 10,000 is invested for one year at a 10% interest. The future value of that money is:
FV = Rs. 10,0000 X [1 + (10%/1)]1x1 = Rs. 11,000
The formula can also be adjusted to obtain the present value of the future total. For instance, the value of Rs. 5,000 to be received after a year, compounded at a 7% interest, is: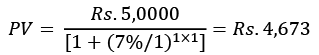
Example 2: To illustrate the concept of the time value of money, let's consider the following scenario. We are considering an investment in a machine that will yield annual cash flows of Rs. 38,500 for the next ten years. The initial cost to acquire the machine is Rs. 2,50,000, and at the end of its useful life, we expect to sell it for Rs. 1,40,000.
- Time Value of Money - NPV Calculation (in Rs)
- Investment Opportunity
- Initial Investment 2,50,000
- Annual Cash Flow 38,500
- Resale Value of Asset after 10 years 1,40,000
We can create a simple schedule to outline our cash flows per period. For simplicity, let's assume zero inflation over the period. We'll start with the initial investment and list the annual cash benefits.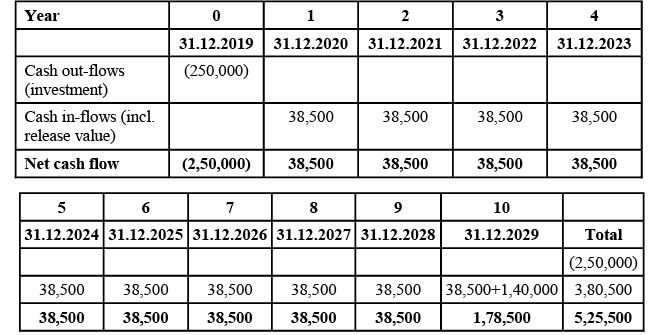
At the conclusion of our table, the cash inflow at the end of the 10th year amounts to Rs. 1,78,500, which incorporates Rs. 1,40,000 from the resale of assets. When viewed in absolute terms, it appears that we will recoup twice the amount we invested over the years. However, to gain a clearer understanding, we need to consider the Time Value of Money. Utilizing the company's Weighted Average Cost of Capital (WACC) as the discount rate is optimal as it accurately reflects the enterprise's true cost of capital. We can proceed to calculate the Net Present Value (NPV) of the cash flows using Excel's more sophisticated NPV computation.
- Discount Factor (WACC) 10 %
- Net Present Value (NPV) 40,622.5
The cash flows of Rs.38,500 here can be considered as an annuity of 10 years of Rs.38,500 and the resale value of Rs. 1,40,000 is to be discounted to the present value. Here we have to find the present value of an annuity of Rs.38,500 of 10 years tenure value occurring after 10 years. Here the discount factor is going to be the weighted average cost of capital (WACC) which is 10%.
Now putting the values in the formula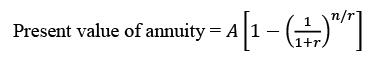
Where 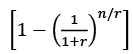 is the present value interest factor from annuity (PVIFArn). This value can be found from the present value interest factor for annuity for 10% discount rate and 10 years, and is 6.145. Therefore, present value of annuity of Rs.38,500 would be 6.145 x 38,500 = 2,36,582.50.
is the present value interest factor from annuity (PVIFArn). This value can be found from the present value interest factor for annuity for 10% discount rate and 10 years, and is 6.145. Therefore, present value of annuity of Rs.38,500 would be 6.145 x 38,500 = 2,36,582.50.
Now let us find the present value of Rs. 1,40,000 going to be received ten years hence from now.
The present value in first factor for discount rate of 10% for 10 years is 0.386, therefore present value of Rs.1,400,000 is going to be:
1,40,000 x .386 = 54,040
The present value of cash flows would be Rs. 2,36,582.50 + Rs. 54,040= Rs. 2,90,622.50
The net present value would be:
2,90,622.5 - 2,50,000 = 40,622.5
Since NPV is positive investment can be accepted.
Financial Decision-Making and the Time Value of Money
The discounted cash flow analysis (DCF), a widely used method for evaluating investment proposals, relies on the concept of the time value of money. This principle is not only integral to financial planning and risk management but also permeates various sectors of finance. Money's worth is contingent on time, constituting a foundational tenet in finance. Money received today holds a different value than money received in the future, owing to the ability to invest and generate returns. For instance, if given the choice between Rs. 100 now and Rs. 100 in a year, Rs. 100 presently holds greater value as it can be invested at a 10% interest rate, yielding a return of Rs. 10. After a year, Rs. 100 would appreciate to Rs. 110.
Investment Decision: Investment decisions entail current cash outlays for anticipated future cash inflows.
- Cash flows, both outflows, and inflows occur at different points in time, making them incomparable as is. To address this, the present value of all cash inflows is determined by discounting them to reflect the time value of money. This present value of cash inflows is subsequently juxtaposed against the current cash outlay or project cost.
For instance, let's consider a project with a cost of Rs. 100,000, expected to yield cash inflows over 3 years. The company's cost of capital or required rate of return stands at 15%. The question arises: Is the project viable under these circumstances?
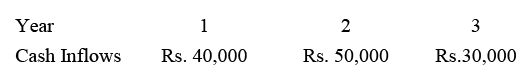
Solution: PV of Cash inflows = PV of Rs 40,000 + PV of Rs 50,000 + PV of Rs 30,000 = [40,000 x 0.870] + [50,000 x 0.756] + [30,000 x 0.658]
= Rs 34,800 + Rs 37,800 + Rs. 19,740 = Rs. 92,340
The present value of cash inflows in this example is Rs 92,340, whereas the project cost is Rs 1 lakh. The project is not acceptable since the benefits are smaller than the costs.
Financing Decision: When a business issues a debenture, it receives immediate cash flow. At the end of each year, interest payments (cash outflows) are due. The debenture amount is redeemed after the period.
As a result, cash inflows come first, followed by cash outflows in the financing choice.
These cash flows cannot be compared because they occur at separate times. Finding the discounted value (present value) of interest payments and the redemption value is used to calculate the time value of the payment. The present value of cash outflows is compared to the debenture selling value, and a decision is made on whether to issue debentures.
Summary
Understanding the concept of the Time Value of Money is crucial for evaluating the true worth of shares and investment prospects in both companies and projects. This principle underlies nearly every financial decision ever made, whether consciously acknowledged or not. It underscores the importance of starting investments early, emphasizing the advantage of receiving money sooner rather than later, known as temporal preference. In essence, the significance of money's time value has been effectively conveyed.
FAQs on Concepts of Value and Return - 1 - Management Optional Notes for UPSC
| 1. What is the future value and how is it calculated? |  |
| 2. How does present value differ from future value? |  |
| 3. What is the significance of the time value of money? |  |
| 4. How is the time value of money calculated? |  |
| 5. How does the time value of money affect financial decision-making? |  |





















