Costing and Budgetary Control Methods: Standard Costing and Variance Analysis - 2 | Management Optional Notes for UPSC PDF Download
| Table of contents |

|
| Examples |

|
| Advantages of Standard Costing |

|
| Limitation / Disadvantages of Standard Costing |

|
| Distinguish between Standard Costing & Budgetary Control |

|
Fixed Overheads Variances
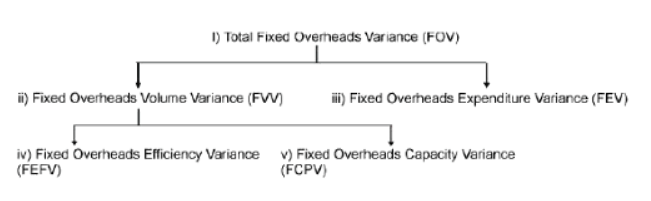 (i) Total Fixed Overheads Variance (FOV) is difference between the standard Fixed Overheads specified for the output achieved and the actual fixed overheads.
(i) Total Fixed Overheads Variance (FOV) is difference between the standard Fixed Overheads specified for the output achieved and the actual fixed overheads.
FOV = Standard Fixed Overheads for standard Hours - Actual Fixed Overheads for Actual Hours
= (SH x SR) - (AH x AR)
When the actual overheads are less than the standard overheads then the fixed overheads variance is favourable and when the actual overheads are more than the standard overheads then the fixed overheads variance is adverse.
This variance is caused by the variations in the volume of actual production and the amount of fixed expenses actually incurred. Therefore, it is classified into -
- Volume Variance and
- Expenditure Variance
(ii) Fixed Overheads volume variance (FVV) is the portion of the total fixed overheads variance due to the difference between the standard volume of output and the budgeted volume of output.
FVV= (Standard Hours - Budgeted Hours) x Standard Rate
= (SH - BH) x SR
When the budgeted hours are less than the standard hours then the Fixed Overheads variance is favourable and when the budgeted hours are more than the standard hours then the fixed overheads variance is adverse it is further divided into
- Fixed Overheads Efficiency Variance
- Fixed Overheads Capacity Variance
(iii) Fixed Overheads Expenditure Variance - (FEV) - is the portion of total fixed overheads variance due to the difference between the budgeted expenditure specified and the actual expenditure.
FEXV = Budgeted Fixed Overheads for Budgeted Hours - Actual Fixed Overheads for Actual Hours
= (BH x SR) - (AH x AR)
When the actual fixed overheads are less than the budgeted fixed overheads then fixed overheads expenditure variance is favourable and vice versa.
(iv) Fixed Overheads Efficiency variance (FEFV) is the portion of fixed overheads volume variance, due to the difference between the standard volume of output specified and the actual volume of output.
FEFV= (Standard Hours - Actual Hours) x Standard Rate
= (SH - AH) x SR
When the actual hours are less than the standard hours then the fixed overheads efficiency variance is favourable and when the actual hours are more than the standard hours then the fixed overheads efficiency variance is adverse.
(v) Fixed overheads Capacity variance (FCPV) - is the portion of fixed overheads volume variance, due to the difference between the actual volume of output specified and the budgeted volume of output.
FCPV= (Actual Hours - Budgeted Hours) x Standard Rate
= (AH - BH) x SR
When the actual hours are less than the budgeted hours then the fixed overheads capacity variance is favourable and when the actual hours are more than the budgeted hours then the fixed overheads capacity variance is adverse.
Varification:
FOV = FVV + FEV
FVV = FEFV + FCPV
Variable Overheads Variances

(i) Total Variable Overheads Variances (VOV) is the difference between the standard variable overheads specified for the output achieved and the actual variable overheads.
VOV = Standard Variable Overheads for Standard Hours - Actual Variable Overheads for Actual Hours
= (SH x SR) - (AH x AR)
When the actual overheads are less than the standard overheads then the variable overheads variance is favourable and when the actual overheads are more than the standard overheads then the variable overheads variance is adverse it is further classified as -
- Efficiency Variance
- Expenditure Variance
(ii) Variable Overheads Efficiency Variances (VEFV) - is the portion of the total variable overheads variance, due to the difference between the standard volume of output specified and the actual volume of output.
VEFV = (Standard Hours - Actual Hours) x Standard Rate
= (SH - AH) x SR
When the actual hours are less than the standard hours then variable overheads efficiency variance is favourable and when the actual hours are more than the standard hours then the variable overheads efficiency variance is adverse.
(iii) Variable Overheads Expenditure Variance (VEXV) is the portion of variable overheads variance due to the difference between the recovered expenditure and the actual expenditure.
VEXV = (Standard Rate - Actual Rate )x Actual Hours
= (SR - AR )x AH
When the actual variable overheads are less than the recovered variable overheads then the variable overheads expenditure variance is favourable and when the actual variable overheads are more than the recovered variable overheads then the variable overheads expenditure variance is adverse.
Verification: VOV = VEFV + VEXV
Examples
Example 1: Material Variances: From the following particulars in respect of a product ‘x’ in which raw materials ‘A’ and ‘B’ are used, calculate.
i) MCV, ii) MPV, iii) MUV, iv) MMV v) MYV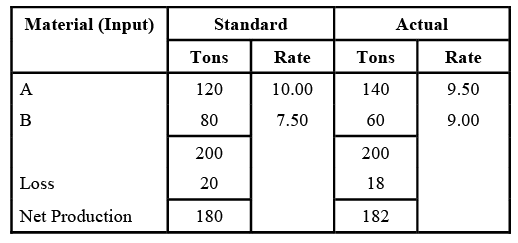 Ans:
Ans:

MCV = (SQ x SP) - (AQ x AP)
A = (121.33 x 10) - (140 x 9.50)
= 1213.3 - 1330 = 116.70 (A)
B = (80.89 x7.50) - (60 x 9)
= 606.68 - 540 = 66.68 (F)
MCV = A + B
= 116.70 (A) + 66.68 (F)
MCV = 50.02 (A)
MPV = (SP - AP) x AQ
A =(10 - 9.50) x 140
= 0.50 x 140
= 70(F)
B = (7.50 - 9.00) x 60
= (1.50) x 60
= 90 ( A )
MPV = A + B
= 70 (F) + 90 (A)
MPV = 20 (A)
MUV = (SQ - AQ) x SP
A =(121.33 -140) x 10
= (18.67) x 10
= 186.7 (A)
B = (80.89 - 60) x 7.50
= 20.89 x7.50
= 156.68 (F)
MUV = A + B
= 186.70 (A) +156.68 (F)
MUV = 30.02 (A)
MYV = ( SQ - RQ )x SP
A =(121.33 -120) x 10
= 1.33 x 10 = 13.3 (F)
B = (80.89 - 80) x 7.50
= 0.89 x7.50
= 6.68 (F)
MYV = A + B
= 13.3 (F) + 6.68 (F)
= 19.98 (F)
MMV = (RQ - AQ) x SP
A =(120 -140) x 10
= ( 20) x 10
= 200(A)
B = (80 - 60) x 7.50
= 20 x7.50
= 150(F)
MMV = A + B
= 200 (A) + 150 (F)
= 50 ( A )
Verification,
MCV = MPV + MUV
50.00 (A) = 20 (A) + 30.02 (A)
50.02 (A) = 50.02 (A)
MUV = MYV + MMV
30.02 (A) = 19.98 (F) + 50 (A)
30.02 (A) = 30.02 (A)
Example 2: Labour Variances: The following details are available from the records of xyz Co, engaged in manufacturing Article x for the month ended on April, 2014.
The standard labour hours and rates of payment were as follows: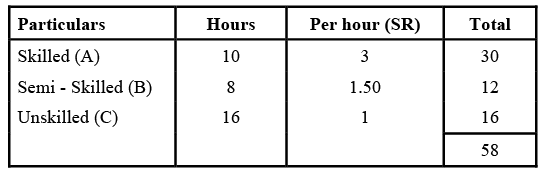 The actual production was 1000 articles ‘x’ for which the actual hours worked and rates are given below:
The actual production was 1000 articles ‘x’ for which the actual hours worked and rates are given below: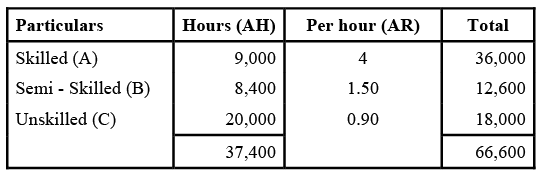 Ans: Standard given for a single product and actual data given for 1000 articles.
Ans: Standard given for a single product and actual data given for 1000 articles.
∴ Standard also take for 1000 articles

LCV = (SH x SR) - (AH x AR)
A =(10000 x 3) - (9000 x 4)
= 30000 - 36000 = 6000(A)
B = (8000 x 1.50) - (8400 x 1.50)
= 12000 -12600 = 600(A)
C = (16000 x 1) - ( 20000 x 0.90)
= 16000 -18000 = 2000(A)
LCV = A + B + C
= 6000 (A) + 600 (A) + 2000 (A) = 8600(A)
LEV = ( SH - AH) x SR
A = (10000 - 9000) x 3 = 1000 x 3 = 3000(F)
B = (8000 - 8400) x 1.50 = (400) x 1.50 = 600(A)
C =(16000 - 20000) x 1 = (4000) x 1 = 4000(A)
LEV = A + B + C
= 3000 (F) + 600 (A) + 4000 (A) = 1600(A)
LRV = (SR - AR)x AH
A =(3 - 4)x 9000 = (l)x 9000 = 9000(A)
B =(1.50 -1.50) x 8400 = 0 x 8400 = NIL
C =(1 - 0.90) x 20000 = 0.10 x 20000 = 2000(F)
LRV = A + B + C
= 9000 (A) + NIL + 2000 (F)
= 7000(A)
LYV = (SH - RH) x SR
A =(10000 -11000) x 3 = (1000) x 3 = 3000(A)
B =(8000 - 8800)x 1.50 = (800) x 1.50 = 1200 (A)
C =(16000 -17600) x 1 = (1600) x 1 = 1600 (A)
LYV = A + B + C
= 3000 (A) +1200 (A) +1600 (A) = 5800(A)
LMV = ( RH - AH )x SR A =(11000 - 9000) x 3
= 2000 x 3 = 6000(F)
B = (8800 - 8400) x 1.50
= 400 x 1.50 = 600(F)
C =(17600 - 20000) x 1
= 2400 (A) x 1 = 2400 (A)
LMV = A + B + C
= 6000 (F) + 600 (F) + 2400 (A) = 4200(F)
Verification:
LCV = LEV + LRV
8600 (A) = 1600 (A) + 7000 (A)
8600 (A) = 8600 (A)
LEV = LYV + LMV
1600 (A) = 5800 (A) + 4200 (F)
1600 (A) = 1600 (A)
Example 3: Both Material & Labour Variances: The Standard Cost of a product Material Cost 2Kg @ Rs. 2.50 each Rs. 5 per unit Wages : 2 hours @ Rs. 1.00 each Rs. 2.00 per unit. The actual which have emerged from business operations are as follows : Production 8000 units Material Consumed 16500 Kg @ Rs. 2.40 each Rs. 39,600.
Wages paid 18000 hours @ Rs. 1.20 each Rs. 21600.
You are required to compute material and labour Variances.
Ans: Note: Standard is given for a product & the actual data is given for 8000 units. So the standard is also converted into 8000 units of production.
SQ = 2Kg per unit × 8000 = 16000 Kgs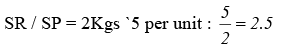
AQ = 16500
AP = 2.40
SH = 2 hours per unit × 8000 = 16000 hours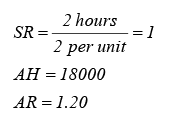
MCV = (SQ x SP) - (AQ x AP)
= (16000 x 2.5)- (16500 x 2.40) = 40000 - 39600 = 400(F)
MPV = (SP - AP) x AQ
= (2.5 - 2.40) x 16500 = 0.10 x 16500 = 1650(F)
MUV = (SQ - AQ) x SP
= (16000 -16500) x 2.5 = (500) x 2.5 = 1250 ( A )
MCV = MPV + MUV
400 (F ) = 1650 (F) + 1250 (A)
400 (F ) = 400 (F)
LCV = (SH x SR) - (AH x AR)
= (16000 x 1)-(18000 x 1.20)
= 16000 - 21600 = 5600(A)
LEV = ( SH - AH) x SR
= (16000 -18000) x 1 = (2000) x 1 = 2000(A)
LRV = (SR - AR)x AH = (1 -1.20) x 18000 = (0.20) x 18000 = 3600(A)
LCV = LEV + LRV
5600 (A) = 2000 (A) + 3600 (A)
5600 (A) = 5600 (A)
Example 4: Fixed Overheads Variance: From the following information, compute fixed overhead cost, Expenditure and Volume Variance : Normal Capacity is 10000 hours, Budgeted Fixed Overhead Rate is Rs. 20 per Standard Hour.
Actual level of capacity utilised is 8800 standard hours. Actual fixed overhead is Rs. 104000
Ans: SH = 8800
Standard Overhead Rate (SR) = 20
Budgeted Hours (BH) = 10000
Actual Fixed Overhead (AFO) = 104000
FOV = (SH x SR)- AFO = (8800 x 20) - 104000 = 176000 -104000 = 72000(F)
Fixed Overheads Expenditure Variance FDEV = (BH x SR) - Actual FO
= (10000 x 20) - 104000 = 200000 - 104000 = 96000(F)
Fixed Overheads Volume Variance (FVV)
= Standard FO - Budgeted FO
= (8800 x 20) -(10000 x 20)
= 176000 - 200000
= 24000(A)
Verification:
FOV = FOEV + FVV
72000 (F) = 96000 (F) + 24000 (A)
Example 5: (Variable Overheads Variances) The following data is given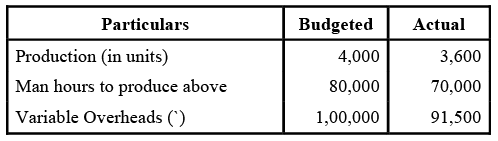
The standard time to produce one unit of the product is 200 hours. Calculate variable overheads variances.
Ans: 
Variable Overhead Variance (VOV)
= (SH x SR)-(AH x AR)
= {72000 x 1.255)-(70000 x 1.307)
= 90000 - 91500 = 1500(A)
Variable Overhead Efficiency Variance (VEFV)
= ( SH - AH) x SR
= {72000 - 70000) x 1.25 = 2000 x 1.25 = 2500(F)
Variable Overhead Expenditure Variance (VEXV)
= ( SR - AR) x AH
= {1.25 -1.307) x 70000 = (0.057) x 70000 = 4000(A)
Verification:
VOV = VEFV + VEXV
1500 (A) = 2500 (F) + 4000 (A)
1500 (A) = 1500 (A)
Advantages of Standard Costing
The advantages of Standard Costing are as follows:
- Cost Control, Reduction, and Increased Profitability: Analysis of variances is beneficial for cost control, cost reduction, and enhancing profitability. It allows businesses to identify areas of inefficiency and take corrective actions.
- Incentive and Motivation: Standards provide incentives and motivation for workers. Employees strive to achieve the set standards, leading to increased efficiency and productivity.
- Prompt Availability of Cost Information: Cost information is readily available under the standard costing system. The promptness of cost information is advantageous for various aspects of costing, such as fixing selling prices and valuing work in progress.
- Contribution to Budgetary Control and Decision Making: Standard costing contributes to budgetary control, helping in the planning and monitoring of budgets. It also aids in decision-making processes by providing relevant cost information.
- Balancing Profits through Valuation of Stock: The valuation of opening and closing stock at standard prices helps balance profits. This enables the preparation of the Profit & Loss Account at regular intervals as needed.
 |
Download the notes
Costing and Budgetary Control Methods: Standard Costing and Variance Analysis - 2
|
Download as PDF |
Limitation / Disadvantages of Standard Costing
The disadvantages of Standard Costing include:
- Difficulty in Setting Standards: Establishing standards is a challenging task. What serves as a standard for one individual may not be suitable for another. Setting current standards can be particularly difficult, and standards may vary among different individuals.
- Rigidity and Unrealistic Nature of Standards: Once set, standards typically remain unchanged for a significant period. This rigidity can be problematic in industries facing fluctuations in product pricing due to frequent changes in material and labor costs. Revising standards is not easy and can be costly.
- Challenges with Setting Appropriate Standards: Setting standards too low may lead to ridicule, while setting them too high can cause frustration and disbelief among workers. Striking the right balance in setting standards is crucial but challenging.
- Limited Applicability for Small Manufacturers: Standard costing is not widely used by small manufacturers, who form a substantial portion of businesses. The method may be perceived as impractical or resource-intensive for smaller enterprises.
- Complexity in Multi-Period Production: Applying standard costing becomes challenging when production spans more than one accounting period. Managing standards over extended production periods introduces complexities in the application of this costing method.
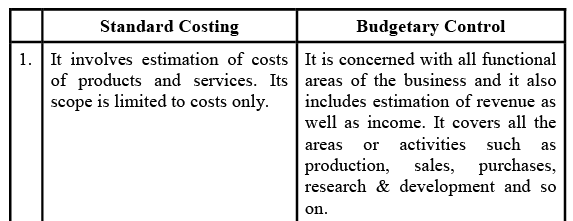
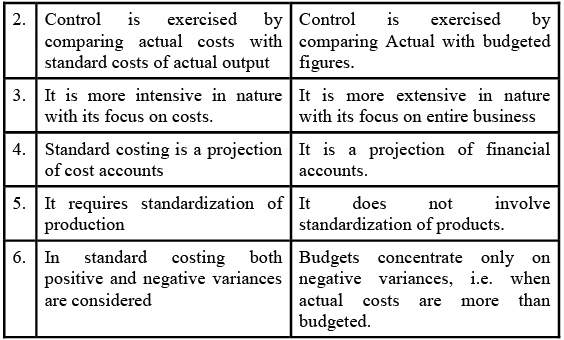
Distinguish between Standard Costing & Budgetary Control
FAQs on Costing and Budgetary Control Methods: Standard Costing and Variance Analysis - 2 - Management Optional Notes for UPSC
| 1. What are the advantages of standard costing? |  |
| 2. What are the limitations of standard costing? |  |
| 3. How does standard costing differ from budgetary control? |  |
| 4. How can standard costing be used for performance evaluation? |  |
| 5. How does standard costing contribute to decision-making? |  |




















