Crystal Field Theory (CFT) | Inorganic Chemistry for NEET PDF Download
What is Crystal Field Theory?
The net change in crystal energy resulting from the orientation of d orbitals of a transition metal cation inside a coordinating group of anions also called ligands.

Basic Idea behind CFT
- Crystal field theory is now much more widely accepted than the valence bond theory. It is assumed that the attraction between the central metal and ligands in a complex is purely electrostatic.
- The transition metal which forms the central atom cation in the complex is regarded as a positive ion of charge equal to the oxidation state.
- It is surrounded by negative ligands or neutral molecules which have a lone pair of electrons If the ligand is a neutral molecule such as NH3, the negative end of the dipole in the molecule is directed toward the metal cation.
- The electrons on the central metal are under repulsive forces from those on the ligands. Thus, the electrons that occupy the d-orbital remain away from the direction of the approach of ligands.
Overview of Crystal Field Theory
In the crystal field theory, the following assumptions are made:
- Ligands are treated as point charges.
- There is no interaction between metal orbitals and ligands orbitals.
- All the d orbitals on the metal have the same energy (that, is degenerate) in the free atom.
However, when a complex, is formed, the ligands destroy the degeneracy of these orbitals, that is, the orbitals now have different energies. In an isolated gaseous metal ion, all five d orbitals have the same energy and are termed degenerate. If a spherically symmetrical field of ligands surrounds the metal ion, the d orbitals remain degenerate. However, the energy of the orbitals is raised because of repulsion between the field of ligands and electrons on the metal. In most transition metal complexes, either six or four ligands surround the metal, giving octahedral or tetrahedral structures. In both these cases, the field produced by the ligands is not spherically symmetrical. Thus, the d orbitals are not all affected equally by the ligand field.
High Spin and Low Spin
The complexion with the greater number of unpaired electrons is known as the high spin complex, the low spin complex contains the lesser number of unpaired electrons. High spin complexes are expected with weak field ligands whereas the crystal field splitting energy is small Δ. The opposite applies to the low spin complexes in which strong field ligands cause maximum pairing of electrons in the set of three t2 atomic orbitals due to large Δo.
- High spin – Maximum number of unpaired electrons.
- Low spin – Minimum number of unpaired electrons.
Example:

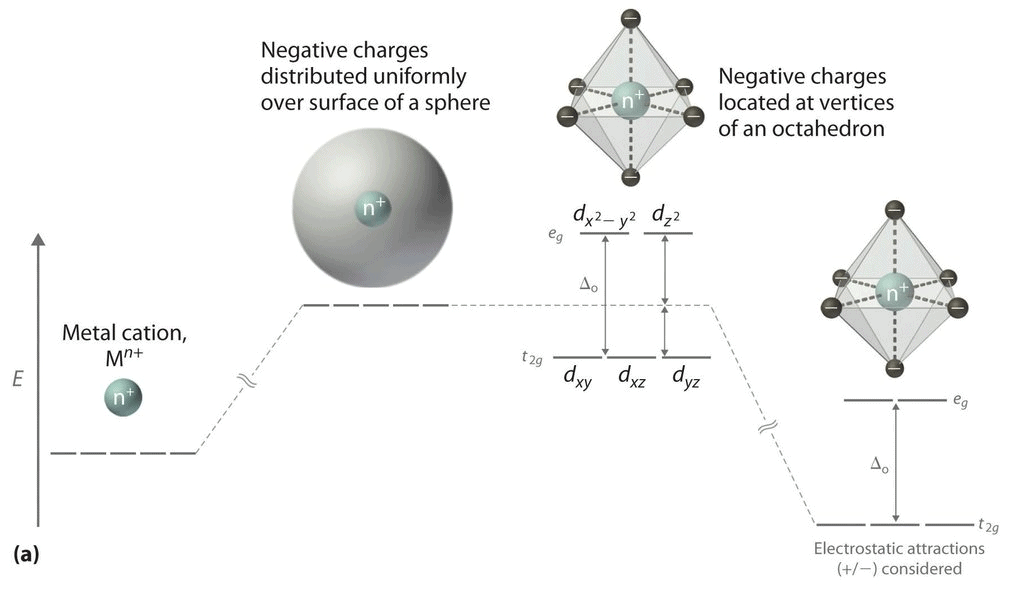
Crystal Field Splitting in Octahedral Complex
In the octahedral complex, the metal is at the centre of the octahedron and the ligands are at the six corners.The direction x, y and z point to three adjacent corners of the octahedron as shown fig.
The lobes of the eg orbitals (dx2-y2 and dz2) point along the axes x,y and z. The lobes of the t2g orbitals (dxy, dxz and dyz) point in between the axes. If follows that the approach of six ligands along the x,y,z, -x, -y, and -z directions will increase the energy of the dx2 - y2 and dz2 orbitals (which point along the axes) then it increases the energy of the dxy, dxz and dyz orbitals (which points between the axes). Thus, under the influence of an octahedral ligand field, the d orbitals split into two groups of different energies.
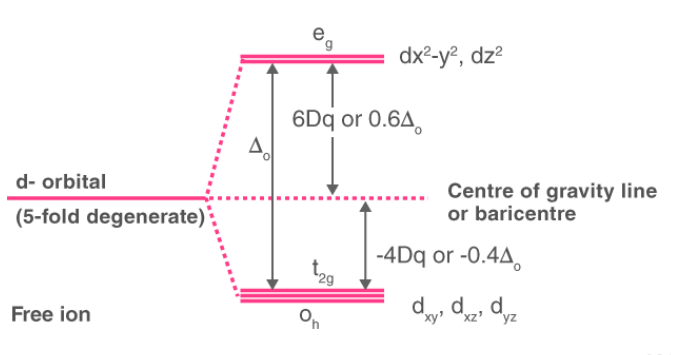
Rather than referring to the energy level of an isolated metal atom. The difference in energy between the two d levels is given by the symbols Δ0 or 10 Δq.?
It follows that the eg orbitals are 0.6 Δ0 above the average level, and the t2g orbitals -0.4 Δ0 below the average level.
Crystal Field Splitting in Tetrahedral Complex
 Relation of the tetrahedron to a cubeA regular tetrahedron is related to a cube. One atom is at the centre of the cube, and four of the eight corners of the cube are occupied by ligands as shown in Fig. The direction x,y and z point to the centres of the faces of the cube. The eg orbitals point along x,y and z (that is, to centres of the faces.)
Relation of the tetrahedron to a cubeA regular tetrahedron is related to a cube. One atom is at the centre of the cube, and four of the eight corners of the cube are occupied by ligands as shown in Fig. The direction x,y and z point to the centres of the faces of the cube. The eg orbitals point along x,y and z (that is, to centres of the faces.)
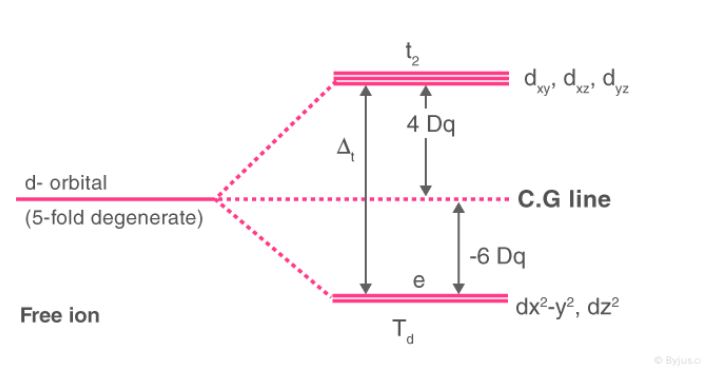
The approach of the ligands raised the energy of both sets of orbitals. The energy of the t2g orbital raised most because they are closest to the ligands. This crystals field splitting is opposite to that in octahedral complexes. The t2g orbitals are 0.4 Δt above the average energy of the two groups (the barycenter) and the eg orbitals are 0.6 Δt below the average level.
Limitations Of Crystal Field Theory
The crystal field theory is highly useful and more significant as compared to the valence bond theory. Even after such useful properties, it has many limitations. The following points will clearly state the limitations of crystal field theory:
- The assumption that the interaction between metal-ligand is purely electrostatic cannot be said to be very realistic
- This theory takes only the d-orbitals of a central atom into account. The s and p orbits are not considered for the study
- The theory fails to explain the behaviour of certain metals which cause large splitting while others show small splitting. For example, the theory has no explanation as to why H2O is a stronger ligand as compared to OH–
- The theory rules out the possibility of having p bonding. This is a serious drawback because is found in many complexes.
- The theory gives no significance to the orbits of the ligands. Therefore, it cannot explain any properties related to ligand orbitals and their interaction with metal orbitals.
Crystal Field Stabilization Energy
In a chemical environment, the energy levels generally split as directed by the symmetry of the local field surrounding the metal ion. The energy difference between the eg and t2g levels is given as or 10Dq. It states that each electron that goes into the lower t2g level stabilizes the system by an amount of -4Dq and the electron that goes into eg level destabilizes the system by +6Dq. That is the t2g is lowered by 4Dq and the eg level is raised by +6Dq.Example: The net change in energy for d5 and d10 systems will be zero as shown below.
d5 :- 3(-4Dq) + 2(+6Dq) = -12Dq + 12Dq = 0
d10 :- 6(-4Dq) + 4(+6Dq) = -24Dq + 24Dq = 0
The decrease in energy caused by the splitting of the energy levels is called the “Ligand Field Stabilization Energy (LFSE)”.
Crystal Field Stabilization Energy Table
| Electronic Configuration | Octahedral Complex | Tetrahedral Complex | ||
| Weak Field (-Dq) | Strong Field (-Dq) | Weak Field (-Dq) | Strong Field (-Dq) | |
| d0 | 0 | 0 | 0 | 0 |
| d1 | 4 | 4 | 6 | 6 |
| d2 | 8 | 8 | 12 | 12 |
| d3 | 12 | 12 | 8 | (18)* |
| d4 | 6 | 16 | 4 | (24)* |
| d5 | 0 | 20 | 0 | (20)* |
| d6 | 4 | 24 | 6 | (16)* |
| d7 | 8 | 18 | 12 | 12 |
| d8 | 12 | 12 | 8 | 8 |
| d9 | 6 | 4 | 4 | 4 |
| d10 | 0 | 0 | 0 | 0 |
Thus, the crystal field splitting depends on the field produced by the ligand and the charge on the metal ion. An experimentally determined series based on the absorption of light by coordination compound with different ligands known as spectrochemical series has been proposed.
Spectrochemical series arranges ligands in order of their field strength as:
I– < Br– < Cl– < SCN– < F– < OH– < C2O42- < H2O < NCS– < EDTA4- < NH3 < en < CN– < CO

Filling of d-orbitals takes place in the following manner; the first three electrons are arranged in t2g level as per Hund’s rule. The fourth electron can either enter into t2g level giving a configuration of t2g4eg0 or can enter the eg orbital giving a configuration of t2g3eg1. This depends on two parameters magnitude of crystal field splitting, Δo and pairing energy, P.
The possibilities of two cases can better be explained as:
(i) Δo > P: Electron enters in the t2g level giving a configuration of t2g4eg0. Ligands producing this configuration are known as strong field ligands and form low spin complexes.
(ii) Δo < P: Electron enters in the eg level giving a configuration of t2g3eg1. Ligands producing this configuration are known as weak field ligands and form high spin complexes.
Stability of Complexes
A complex is formed in several steps. Each process step is reversible and the equilibrium constant is known as the stepwise formation constant. Let us consider the formation of complex ML4.

The overall formation constant or stability constant, β = K1 × K2 × K3 × K4 and 1/β = Instability constant
Factors affecting the stability of complex compounds :
(i) The values of stability constant differ widely depending on the nature of the metal ion and the ligand In general higher the charge density on the central ion. The greater the stability of its complexes.
(ii) the more basic a ligands, the greater is the ease with which it can donate its lone pairs of electrons and therefore, greater is the stability of the complexes formed by it.
Example: The cyano and ammine complexes are far more stable than those formed by halide ions. This is due to the fact that NH3 and CN- are strong Lewis bases.
(iii) The higher the oxidation state of the metal, the more stable is the complex. The charge density of Co3+ ion is more than Co2+ ion and thus, [Co(NH3)6]3+ is more stable than [Co(NH3)6]2+. Similarly, [Fe(CN)6]3- is more stable than [Fe(CN)6]4-.
(iv) Chelating ligands form more stable complexes as compared to monodentate ligands.
Colour of Complexes
Complexes in which central transition metal ion contains unpaired electrons show colour.

It is ‘d – d’ transition. The colour of complexes depends upon:
- Number of unpaired electrons in transition metal ion
- Nature of ligands
- The oxidation state of central transition metal ion
- The wavelength of light absorbed and emitted
- The proportion of ligands in the coordination sphere
Example: [Ni(H2O)6]+2+ en(aq) → [Ni(H2O)4en]+2 (Green Pale blue)
|
74 videos|106 docs|111 tests
|
FAQs on Crystal Field Theory (CFT) - Inorganic Chemistry for NEET
| 1. What is Crystal Field Theory? |  |
| 2. How does Crystal Field Theory explain the splitting of energy levels in octahedral complexes? |  |
| 3. How is Crystal Field Stabilization Energy calculated in Crystal Field Theory? |  |
| 4. What are the limitations of Crystal Field Theory? |  |
| 5. How does Crystal Field Theory explain the stability of complexes? |  |

|
Explore Courses for NEET exam
|

|


















