DC Pandey Solutions: Interference and Diffraction of Light | Physics Class 12 - NEET PDF Download
Introductory Exercise 29.1
Ques 1: In YDSE, D = 1.2 m and d = 0.25 cm. The slits are illuminated with coherent 600 nm light. Calculate the distance y above the central maximum for which the average intensity on the screen is 75% of the maximum.
Sol:
= 48 × 10-6 m = 48 μm
Ques 2: A possible means for making an airplane invisible to radar is to coat the plane wit h an ant i reflective polymer. If radar waves have a wavelength of 3.00 cm and the index of refraction of the polymer is μ =1.5. How thick is the oil film? Refractive index of the material of airplane wings is greater than the refractive index of polymer.
Sol: 2μt = λ/2 (See the extra points)
This is the condition for destructive interference.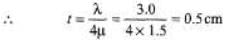
Ques 3: Slit 1 of a double slit is wider than slit 2, so that the light fro m slit 1 has an amplitude three times that of the light fro m slit 2. Show that Eq. (xii) in article 29.4 is replaced by the equation,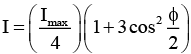
Sol: A1 = 3A2
So, I1 = 9I2
Let A2 = A0 and I2 = I0
Then A1 = 3A0 and I1 = 9I0
and Imax = 16 I0
Now, I = I1 + I2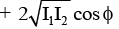
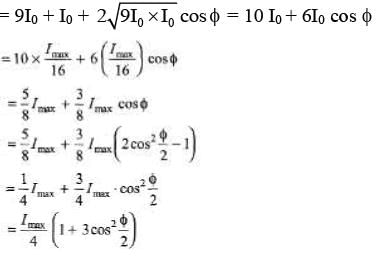
Ques 4: Determine what happens to the double slit interference pattern if one of the slits is covered with a thin, transparent film whose thickness is 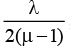 where λ is the wavelength of the incident light and μ is the index o f refraction o f the film.
where λ is the wavelength of the incident light and μ is the index o f refraction o f the film.
Sol: Path difference produced by slab,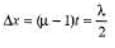
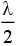 path difference is equivalent to 180° phase difference.
path difference is equivalent to 180° phase difference.
Hence, maximas and minimas interchange their positions.
Ques 5: Two slit s 4.0 × 10-6 m apart are illuminated by light of wavelength 600 nm. What is the highest order fringe in the interference pattern?
Sol: Δx = d sin θ = nλ
Highest integer in Δ6.
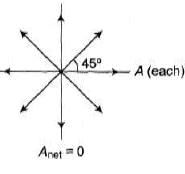
Ques 6: Consider an interference experiment using eight equally spaced slit s. Determine the smallest phase difference in the waves from adjacent slits such that the resultant wave has zero amplitude.
Sol:
Exercises
For JEE Main
Subjective Questions
Energy Distribution in Interference
Ques 1: Two waves of the same frequency and same amplitude a are reaching a point simultaneously. What should be the phase difference between the waves so that the amplitude of the resultant wave be :
(i) 2a (ii) √2a (iii) a and (iv) zero?
Sol:
Ques 2: Two waves of equal frequencies have their amplitude in the ratio of 5 :3. They are superimposed on each other. Calculate the ratio of the maximum to minimum intensities of the resultant wave.
Sol: Amax =5 + 3 = 8 units
Amin = 5 - 3 = 2 units
∴ 
Ques 3: In a Young's double slit experiment λ = 500 nm, d = 1.0 mm and D = 1.0m. Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
Sol: 

= 1.25 × 10-4 m
Ques 4: In a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
Sol: (a) See the hint of above example. At half intensit y,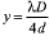
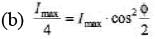
∴ 
or 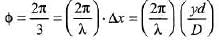
∴ 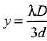
Ques 5: In a two-slit interference pattern, the maximum intensity is I0.
(a) At a point in the pattern where the phase difference between the waves from the two slits is 60°, what is the intensity?
(b) What is the path difference for 480 nm light from the two slits at a point where the phase angle is 60°?
Sol: 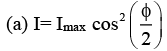
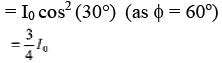
(b) 60° phase difference is equivalent to λ/6 path difference.
Conditions for Interference
Ques 6: Two coherent sources A and B of radio waves are 5.00 m apart . Each source emits waves with wavelength 6.00 m. Consider points along the line between the two sources. At what distances, if any, from A is the interference (a) constructive, (b) destructive?
Sol: (a) At centre path difference is zero. Therefore construction interference will be obtained.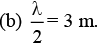 At a distance, where path difference is λ/2 or 3m destructive interference will be obtained.
At a distance, where path difference is λ/2 or 3m destructive interference will be obtained.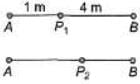
At P1 BP1 - AP1 = 3rn = λ/2
At P2 AP2 - BP2 = 3m = λ/2
Ques 7: A radio transmitting station operating at a frequency o f 120 MHz has two identical antennas that radiate in phase. Antenna B is 9.00 m to the right of antenna A. Consider point P between the antennas and along the line connecting them, a horizontal distance x to the right of antenna A. For what values of x will constructive interference occur at point P?
Sol: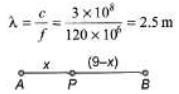
Δx = (BP - AP) = (9 - 2x) = nλ
∴ 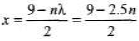
Now, substituting n = 1, 2, ...... etc. We can find different values of x.
x1 = 3.25 m for n = 1
x2 = 2.0m for n = 2
and
x3 = 0.75 m for n = 3
Similarly we will get three points at same distance from other point B.
Young’s Double Slit Experiment
Ques 8: Coherent light from a sodium-vapour lamp is passed through a filter that blocks every thing except for light of a single wavelength. It then falls on two slits separated by 0.460 mm. In the resulting interference pattern on a screen 2.20 m away, adjacent bright fringes are separated by 2.82 mm. What is the wavelength?
Sol: 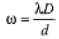
∴ 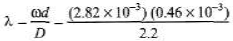
= 0.589 × 106m = 0.590 nm
Ques 9: Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is 2.0 x 10-3m.
Sol: 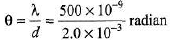
≈ 0.014°
Ques 10: A Young's double slit apparatus has slits separated by 0.25 mm and a screen 48 cm away from the slit s. The whole apparatus is immersed in water and the slit s are illuminated by the red light ( λ = 700 nm in vacuum). Find the fringe-width of the pattern formed on the screen. (μw = 4/3)
Sol: Wavelength in water 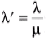
Fringe width 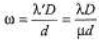
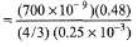
= 10-3 m = 1 mm
Ques 11: In a two-slit experiment with monochromatic light, fringes are obtained on a screen place d at some distance from the slits. If the screen is moved by 1.5 × 10-2 m towards the slits, the change in fringe-width is 3 × 10-5 m. If the distance between the slits is 10-3 m, calculate the wavelength of the light used.
Sol: 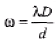
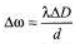
∴ 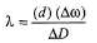
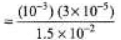
= 2.0 × 10-6 m = 2.0 μm
Ques 12: In a double slit experiment the distance between the slits is 5.0 mm and the slit s are 1.0 m from the screen. Two interference patterns can be seen on the screen one due to light with wavelength 480 nm, and the other due to light with wavelength 600 nm. What is the separation on the screen between the third order bright fringes of the two interference patterns?
Sol: Distance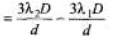

= 7.2 × 10-5m = 0.072 mm
Ques 13: Two slits spaced 0.450 mm apart are placed 75.0 cm from a screen. What is the distance between the second and third dark lines of the interference pattern on the screen when the slits are illuminated with coherent light with a wavelength of 500 nm?
Sol: The required distance = one fringe width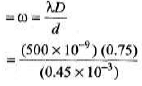
= 8.33 × 10-4 m = 0.83 mm
Ques 14: Coherent light with wavelength 600 nm passes through two very narrow slits and the interference pattern is observed on a screen 3.00 m fro m the slit s. The first -order bright fringe is at 4.94 mm from the centre of the central bright fringe. For what wavelength of light will the first-order dark fringe be observed at this same point on the screen?
Sol: 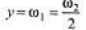
∴ 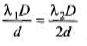
⇒ λ2 = 2λ1 = 1200 nm
Ques 15: Two very narrow slits are spaced 1.80 μm apart and are placed 35.0 cm from a screen. What is the distance between the first and second dark lines of the interference pattern when the slits are illuminated with coherent light of λ = 550 nm? (Hint: The angle θ is not small).
Sol: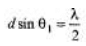
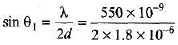
∴
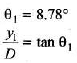
∴ y1 = D tan θ1
= 35 tan 8.78° = 5.41 cm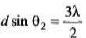
∴ 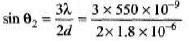
∴ θ2 = 27.27°
y2 = D tan θ2
= 35 tan 27.27°
= 18 cm
Δy = y2 - y1 = 12.6 cm
|
98 videos|332 docs|102 tests
|
FAQs on DC Pandey Solutions: Interference and Diffraction of Light - Physics Class 12 - NEET
| 1. What is interference of light? |  |
| 2. How does interference of light occur? |  |
| 3. What is the difference between interference and diffraction of light? |  |
| 4. What are the applications of interference and diffraction of light? |  |
| 5. How can interference and diffraction be observed in everyday life? |  |






















