DC Pandey Solutions: Modern Physics II | Physics Class 12 - NEET PDF Download
Introductory Exercise 31.1
Ques 1: Activity of a radioactive substance decreases from 8000 8q to 1000 Bq in 9 days. What is the half life and average life of the radioactive substance?
Sol: 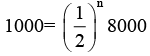
∴ n = 3 = number of half lives There half lives are equivalent to 9 days. Hence one half life is 3 days.
tav = 1.44 t1/2 = 1.44 × 3 = 4.32 days
Ques 2: A radioactive substance has a half-life of 64.8 h. A sample containing this isotope has an initial activity (t = 0) of 40 μCi. Calculate the number of nuclei that decay in the time interval between t1 = 10.0 hand t2 =12.0 h.
Sol: R0 = λN0
⇒ 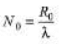
where, 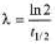
N = Noe-λt
Find N1 = Noe-λt
and N2 = Noe-λt
Number of nuclei decayed in given time= N1 N2
Ques 3: A freshly prepared sample of a certain radioactive isotope has an activity of 10 mCi. After 4.0 h its activity is 8.00 mCi.
(a) Find the decay constant and half life
(b) How many atoms of the isotope were contained in the freshly prepared sample?
(c) What is the sample's activity 30.0 h after it is prepared?
Sol: (a)R = R0e-λt
R0 - 20 mci
R = 8 mci
t = 4.0 h Find λ.
(b) R0 =λN0
Find. 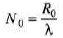
(c) Find R = R0e-λt
Ques 4: A radioactive substance contains 1015 atoms and has an activity of 6.0 × 1011 Bq. What is its half-life?
Sol: R0 = λN0
6.0 × 1011 = λ(1015)
∴ λ = 6.0 × 10-4 s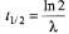

Ques 5: Two radioactive elements X and Y have half-life periods of 50 minutes and 100 minutes respectively. Initially both of them contain equal number of atoms. Find the ratio of atoms left NX/NY after 200 minutes.
Sol: In 200 minute time,
n1 = number of half lives of X
= 200/50 = 4
n2 = number of half lives of Y
= 200/100 = 2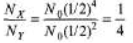
Introductory Exercise 31.2
Ques 1: (a) How much mass is lost per day by a nuclear reactor operated at a 109 watt power level?
(b) If each fission releases 200 MeV, how many fissions occur per second to yield this power level?
Sol: (a)m(c)2 =P x t
∴ 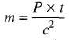
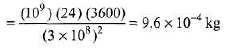
(b) Number of fissions required per second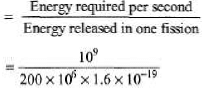
= 3.125 × 1019
Ques 2: Find energy released in the alpha decay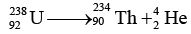
Given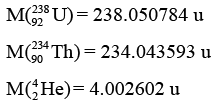
Sol: Mass defect ∑mi - ∑mf = Δm
= (238.050784) - (234.043593 + 4.002602) = 4.589 × 10-3 u
Energy released = Δm × 931.48 MeV = 4.27 MeV
Exercises
For JEE Main
Subjective Questions
Radioactivity
Ques 1: The disintegration rate of a certain radioactive sample at any instant is 4750 disintegrations per minute. Five minutes later the rate becomes 2700 per minute. Calculate
(a) decay constant and
(b) half-life of the sample
Sol: (a) R = R0e-λt
R = 2700 per minute, R0 = 4750 per minute t = 5 minute
Find λ.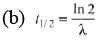
Ques 2: A radioactive sample contains 1.00 × 1015 atoms and has an activity of 6.00 × 1011 Bq. What is its half-life?
Sol: R = λN
6 × 1011 =1.0 × l015λ
λ= 6 × 10-4s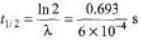 = 1155 s= 19.25 min
= 1155 s= 19.25 min
Ques 3: Obtain the amount of 60 Co necessary to provide a radioactive source of 8.0 Ci strength. The hal-flife of 60Co is 5.3 years?
Sol: R = λN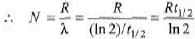
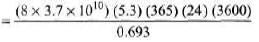
= 7.14 × 1019
Ques 4: The half-life of 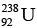 gainst alpha decay is 4.5 × 109 year. How much disintegration per second occurs in 1 g of
gainst alpha decay is 4.5 × 109 year. How much disintegration per second occurs in 1 g of 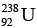 ?
?
Sol: 
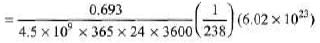
= 1.23 x 104dps 5. 1/λ = 10days
∴ λ = 0.1 day-1
Probability of decay
= 1 – e-λt = 1 - e-0.1×5 = 0.39
Ques 5: In an ore containing Uranium, the ratio of 238U to 206Pb nuclei is 3. Calculate the age of the ore, assuming that all the lead present in the ore is the final stable product of 238U. Take the half-life of 238U to be 4.5 × 109 years.
Sol: 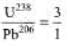
N0 = 3 + 1 = 4 N =3
From Eqs. (i) and (ii), we get t = 1.88 × 109yr
Ques 6: The half-lives of radioisotopes P32 and P33 are 14 days and 25 days respectively. These radioisotopes are mixed in the ratio of 4 :1 of their atoms. If the initial activity of the mixed sample is 3.0 m Ci, find the activity of the mixed isotopes after 60 year.
Sol: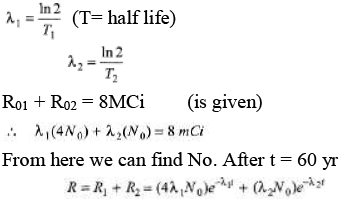
Ques 7: Consider two decay reactions.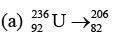 Pb+ 10 protons + 20 neutrons
Pb+ 10 protons + 20 neutrons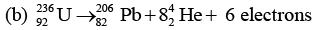
Are both the reactions possible?
Sol: (a) 82 + 10 = 92, 206 + 10 + 20 = 236
So this reaction is possible.
(b) 82 + 16 - 6 = 92, 206 + 32 = 238
But antineutrino is also emitted with β~1 (or electron) decay.
Ques 8: Obtain the binding energy of a nitrogen nucleus from the following data :
mH = 1.00783 u, mN = 1.00867 u, m(147 N) = 14.00307 u
Give your answer in units of MeV. [Remember 1 u = 931.5 Me V/c2]
Sol: Binding energy = Δm × 931.5 MeV
= (7 × 1.00783 + 7 × 1.00867-14.00307) 931.5 = 104.72 MeV
|
74 videos|314 docs|88 tests
|
FAQs on DC Pandey Solutions: Modern Physics II - Physics Class 12 - NEET
| 1. What are the key topics covered in DC Pandey Solutions: Modern Physics II? |  |
| 2. How can DC Pandey Solutions: Modern Physics II help me prepare for my physics exam? |  |
| 3. Are the solutions in DC Pandey Solutions: Modern Physics II easy to understand? |  |
| 4. Can DC Pandey Solutions: Modern Physics II be used for self-study? |  |
| 5. Is DC Pandey Solutions: Modern Physics II suitable for competitive exams like JEE and NEET? |  |
















