Decision Theory | Management Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Certain Key Issues in Decision Theory |

|
| Marginal Analysis |

|
| Decision Tree Approach |

|
| Preference Theory |

|
| Other Approaches |

|
| Conclusion |

|
Introduction
- Decision-making permeates every aspect of our lives, prompting the exploration of various decision problems and the quest for sound decisions across different epochs and disciplines. This widespread need for effective decision-making has spurred the development of Decision Analysis literature. The diversity of decision problems necessitates a classification framework, facilitating the organization of this extensive literature.
- A fundamental requirement for defining a decision problem is the existence of alternative courses of action, each leading to distinct outcomes, the knowledge of which may vary from known to unknown. This variability in information about outcomes has led to two broad classifications: a) Decision Making under certainty, where outcomes are deterministic and known with certainty, and b) Decision Making under uncertainty, where outcomes are probabilistic and may involve known or unknown probabilities. The study of decision problems in uncertain environments has given rise to Decision Theory.
- Given our foundation in Probability Theory, we are well-equipped to delve into the study of Decision Theory in this unit. The aim of this unit is to explore various methods for addressing decision problems under uncertainty, each method addressing key issues inherent in such problems. Thus, in the subsequent sections, we will first examine these key issues and then proceed to present different methods aimed at resolving them.
Certain Key Issues in Decision Theory
- Various issues emerge when analyzing decision problems under uncertain conditions of outcomes. Firstly, decisions can be perceived as either independent actions or as part of a sequence of decisions made over time. Depending on the planning horizon and the nature of decisions, this leads to either a single-stage or sequential decision problem. In reality, decision-makers often operate within a continuous sequence of decisions, making the problem combinatorial and challenging to solve. However, valid assumptions can often reduce the complexity of the problem and render it manageable.
- The second issue pertains to selecting a criterion for decision-making in these scenarios. Previously, we utilized 'Expected Profit' as our decision criterion. Both Marginal Analysis and the Decision Tree Approach adopt this criterion. However, 'Expected Profit' or 'Expected Monetary Value' (EMV) lacks consideration for the decision-maker's risk attitude. Preference Theory offers a solution by allowing us to incorporate risk preferences into the decision-making process. Another limitation of EMV is its reliance on known probabilities of outcomes. In cases where probabilities are unknown, one approach is to assign equal probabilities to outcomes and then utilize EMV for decision-making. However, this may not always be rational, and alternative criteria exist for such situations.
For the scope of this unit, we will address the aforementioned issues in Decision Theory by studying the following topics:
- Marginal Analysis for single-stage decision problems.
- Decision Tree Approach for sequential decision problems.
- Preference Theory.
- Alternative approaches for problems with unknown probabilities. These topics will be discussed in the subsequent sections in the order presented.
Marginal Analysis
- Marginal Analysis delves into the assessment of whether adding an extra unit is beneficial amidst a multitude of uncertain outcomes associated with various alternative courses of action. The complexity of computations escalates notably when the number of potential values for a random variable increases. For instance, revisiting the example of the newspaper vendor discussed in section 6.4, if the demand could span twenty values with differing probabilities for each value, the computation would become exceedingly laborious. In such scenarios, Marginal Analysis proves to be a valuable tool.
- In this section, we elucidate the underlying concept of Marginal Analysis through Example 1 from section 6.4, with a slight modification. Let's assume that based on historical data, the newspaper vendor determines that demand can range from 31 to 50 copies, with each value having an equal probability of occurrence. The objective is to determine the optimal number of copies to order.
- Marginal Analysis proceeds by scrutinizing whether ordering an additional unit is advantageous. Specifically, we consider ordering X copies, ensuring that ordering the Xth copy is beneficial while ordering the (X+1)th copy is not. To ascertain the viability of ordering X copies, we examine two potential outcomes contingent upon two events: A) the copy being sold, and B) the copy remaining unsold. The Xth copy is sold only if demand equals or exceeds X; otherwise, it remains unsold. In the event of a sale (event A), a profit of 50 p. is accrued from the additional copy, whereas in the event of an unsold copy (event B), a loss of 30 p. is incurred.
These profit and loss margins are specific to the additional or marginal unit, hence termed as marginal profit or loss, leading to the analysis being labeled as Marginal Analysis.
K1 = Marginal profit = 50p
K2 = Marginal loss = 30p
P(A) = Probability ( Demand ≥ X) = 1 -Probability (Demand ≤ X− 1 ). P(B) = Probability ( Demand < X) = Probability (Demand ≤ X− 1 ).
We can write down the expected marginal profit and expected marginal loss as
- Expected Marginal Profit = K1P(A)
- Expected Marginal Loss = K2P(B)
Ordering the Xth copy is worthwhile only if the expected profit due to it is more than the expected loss, so that
K1P(A) > K2P(B)
Now, if F(D) denotes the c.d.f. of demand, then by definition, Probability
Demand < (X - 1) ± F(X - 1)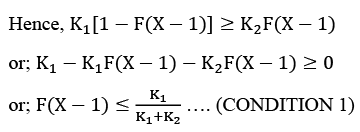
Thus, if condition 1 holds good, it is worthwhile to order the Xth copy. If the optimal decision is to order X copies, then ordering the (X+1)th copy will not be worthwhile, i.e. the expected marginal profit due to the (X+1)th copy should be less than the expected loss.
Proceeding with the analysis in the same way as above, we have:
Expected Marginal Profit = K1 Probability (Demand ≥ X+ 1)
= K1[1-F(X)]
Expected Marginal Loss = K2 F(X)
For the (X+l)th copy : K1[l - F(X)] < K2F(X)
From conditions (1) and (2) and the definition of Fractile, it is clear that X will be the 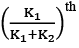 the fractile of the Demand distribution. Thus, for our problem, given the above result, all that we have to do is to calculate
the fractile of the Demand distribution. Thus, for our problem, given the above result, all that we have to do is to calculate 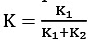 and the Kth fractile of the distribution, which will give us the rquired answer.
and the Kth fractile of the distribution, which will give us the rquired answer.
In our problem :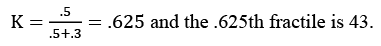
∴ The optimal decision is to order 13 copies.
- We can verify quickly that in the problem given in section 10.4, the ,625th fractile of the demand distribution is 33. So the optimal decision there is to order 33, which is the answer that we have obtained there.
- The above shows how marginal analysis helps us in arriving at the optimal decision with very little computation. This is especially useful when the random variable of interest takes a large number of values. Though we have demonstrated this for a discrete demand distribution the same logic can be shown to be applicable for continuous distributions also. Instead of the distribution we have taken, if we would have assumed that demand is normal with a specific n and o, then also the same Kth fractile of N(n, a) would have given us the optimal decision.
Decision Tree Approach
- In the preceding section, we examined a single-stage decision problem. Frequently, decision-makers encounter situations where decisions must be made sequentially, with later decisions contingent upon earlier ones. This sequence may either be inherent or can be orchestrated to optimize decision-making. For instance, consider the recurring production decision for an item with uncertain demand, such as refrigerators.
- Each period necessitates a decision on the production quantity, considering the uncertainties in demand across different periods. Consequently, multiple decisions must be made for each period, with intervening uncertainties influencing outcomes between any two periods. In such cases, the sequence of decisions is inherent.
- In contrast, there are scenarios where decision timeframes permit the exploration of additional information-gathering methods before arriving at the final decision. For example, before launching a product nationwide, conducting test marketing can provide valuable insights. Similarly, in a production setting where a machine produces an unknown percentage of defective units, purchasing a special attachment capable of reducing defects to a known low fraction is an option. The decision then hinges on weighing the risks of not purchasing the attachment against its cost. In such cases, an infinite sequence of decisions can be orchestrated by incorporating sampling from the current process to ascertain the percentage of defectives. At each stage, two alternatives exist: a) purchasing, and b) abstaining from purchase and opting for sampling. This process continues until a decision to cease sampling is made due to various factors, such as prohibitive sampling costs.
- The Decision Tree Approach offers a valuable framework for analyzing such sequential decision problems. We illustrate this approach through an example, often exemplified by the oil drilling scenario, which has been widely explored by numerous authors.
Example I
- Consider the scenario where a decision must be made regarding oil drilling in a specific region, a dilemma faced by our decision-maker. According to the geologist's report, there is a known probability of 0.6 for finding oil in the region. Initially, the decision-maker possesses Rs. 1.5 lakh. The potential outcomes of drilling and discovering oil, versus drilling and finding no oil, are associated with cash reserves of Rs. 5 lakh and Rs. 40,000, respectively. Furthermore, the decision-maker has the option to conduct a seismic test to enhance their understanding of the region's oil content. This test incurs a cost of Rs. 5,000; however, its benefit lies in its predictive accuracy: if oil is present, the test correctly predicts it 90% of the time, while if no oil is present, it is predicted accurately 70% of the time. The question arises: what should be done, and why?
- To address this, the first step involves structuring the decision problem. In the Decision Tree Approach, a square symbolizes an action or decision point, while a circular symbol represents uncertainty. Initially, the alternative courses of action emanate from the decision point, followed by the possible outcomes corresponding to each decision stemming from the uncertainty point. The associated probabilities and consequences for each outcome are listed alongside. This resulting graphical representation is termed a Decision Tree.
- In our example, we start with two potential actions: 1) Undertake the Seismic Test, and 2) Abstain from the Seismic Test. If the test is conducted, it may predict the presence or absence of oil, both of which are uncertain outcomes due to the imperfect nature of the test. Upon knowing the test results, the decision-maker must once again decide whether to proceed with drilling. The corresponding outcomes are known in this scenario as well. Similarly, if the decision is made not to conduct the test, the choice to drill or not must still be made. Thus, the Decision Tree can be represented as follows:
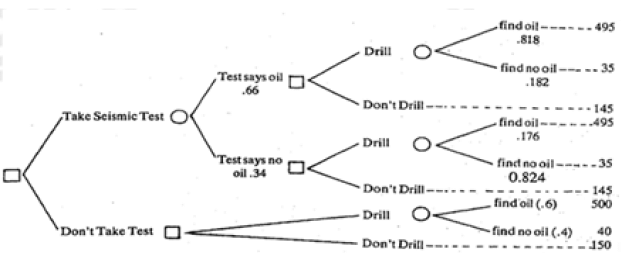
- The values provided alongside each outcome represent amounts in thousands of rupees. The subsequent step involves assigning probabilities to each outcome. If the test is not conducted, the likelihood of finding oil is directly derived from the geologist's report as 0.6. Hence, the probability of not finding oil is calculated as 1 - 0.6 = 0.4. These probabilities can then be associated with each outcome along with the corresponding consequences of 500 and 40 thousand rupees.
- However, once the test is administered, the probabilities of the test yielding positive (indicating the presence of oil) or negative (indicating no oil) results are dependent on the predictive accuracy of the test and must be computed. Similarly, the probability of finding oil given a positive test result is expected to exceed 0.6. These and related probabilities need to be calculated as well. Probability calculations can be performed using Bayes' Theorem.
Utilizing the same notation, two mutually exclusive and exhaustive events, A and B, can be defined as follows:
- Finding oil
- Not finding oil
Other events defined within the context of the same experiment include:
- Test predicts oil is present (positive results)
- Test predicts no oil is present (negative results)
The provided data includes:
- P(A): Probability of finding oil = 0.6
- P(B): Probability of not finding oil = 0.4
- P(C/A): Probability of test correctly predicting oil presence = 0.9
- P(D/A): Probability of test incorrectly predicting oil absence = 0.1
- P(D/B): Probability of test correctly predicting oil absence = 0.7
- P(C/B): Probability of test incorrectly predicting oil presence = 0.3
We are interested in determining:
- P(C): Probability of test predicting oil presence
- P(D): Probability of test predicting no oil presence
- P(A/C): Probability of finding oil given positive test results
- P(A/D): Probability of finding oil given negative test results
- P(B/C): Probability of not finding oil given positive test results
- P(B/D): Probability of not finding oil given negative test results
Bayes' Theorem can be applied for these calculations.

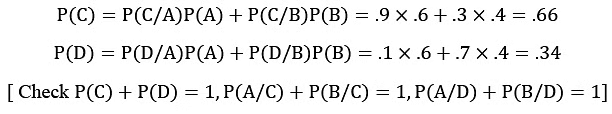
These probabilities are integrated into the decision tree diagram. The final step involves determining the Expected Monetary Value (EMV) for each decision. Beginning from the Northeast corner of the diagram, we "fold back" the tree as follows: The top-right decision is "to drill," with potential outcomes of finding oil or not finding oil, with probabilities of occurrence being 0.818 and 0.182 respectively. The associated contributions are Rs. 4,95,000 and Rs. 35,000 respectively.
Therefore, the EMV of the decision to drill is calculated as follows:
- EMV of decision to drill = (4,95,000 × 0.818) + (35,000 × 0.182) = Rs. 4,11,280
- Since this value exceeds the payoff for not drilling (Rs. 1,45,000), we conclude that drilling is the preferable option once the test indicates the presence of oil, with the corresponding expected payoff being Rs. 4,11,280.
- Similarly, when the test indicates no oil, we find that "not drilling" is the superior option compared to "drilling," as the expected payoff for the former (Rs. 1,45,000) exceeds that of the latter (0.176 × 4,95,000 + 0.824 × 35,000 = Rs. 1,15,960). Thus, the original diagram is simplified as demonstrated.
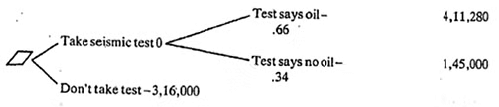
- If the test is not conducted, the expected payoff from drilling is calculated as follows: 500 × 0.6 + 40 × 0.4 = Rs. 3,16,000. Since this exceeds the payoff for not drilling (Rs. 1,50,000), it is advisable to proceed with drilling if the test has not been conducted, as depicted in the diagram.
- Next, we determine the Expected Monetary Value (EMV) of conducting a seismic test: 0.66 × Rs. 4,11,280 + 0.34 × Rs. 1,45,000 = Rs. 3,20,745. Therefore, since this payoff exceeds what one can anticipate if the test is not conducted, it is preferable to undergo the test. Thus, the decision is to "Take the Test." If the test indicates no oil, drilling should be abstained from; however, if the test results are positive, drilling should proceed. This decision strategy maximizes the EMV.
Activity D
- ABC Company operates as a small-scale manufacturer of L.P. records, with the record industry largely monopolized by a Kolkata-based company named XYZ. ABC's ability to persist in this competitive landscape can be credited to their skilled and experienced Managing Director, Mr. A. Given that all the top artists are contracted with XYZ, ABC's strategy revolves around discovering new talents for recording purposes. Mr. A's intuition in this regard has proven invaluable, as he actively engages in the recruitment of fresh talent, with a belief that 70% of his recruits have the potential for national success.
- Once a new talent is identified, a demo tape is produced, and an initial batch of 5,000 records is manufactured for test marketing. Experience has shown that when a recruit achieves national success, the test marketing accurately predicts this outcome 90% of the time. Conversely, when a recruit fails to achieve national success, the test marketing accurately predicts this outcome 70% of the time. Based on the results of the test marketing, a decision is made whether to proceed with national marketing, which involves producing 50,000 records. The artist receives a payment of Rs. 5,000 upon the completion of the demo tape. The variable production cost per record for batches of 5,000 and 50,000 units amounts to Rs. 13 and Rs. 10 respectively, while the selling price is Rs. 40 per record.
- Mr. A is contemplating entering the ghazal market and has already recruited a ghazal singer. However, he anticipates that the predictive capability of test marketing for ghazals will be lower. He estimates that the test marketing will correctly predict success only 70% of the time (down from 90% previously), and in the case of failure, it will only predict correctly 60% of the time (down from 70% previously). Given this reduced predictive accuracy, he is uncertain about the value of conducting test marketing. Can you assist him in making this decision? For practical purposes, success in both test and national marketing implies selling 5,000 and 50,000 records respectively, while failure in either case results in zero sales.
Preference Theory
- Up to this point, our decision-making process has been centered around maximizing the EMV or expected payoff criterion. However, this approach fails to consider the decision maker's risk attitude. In situations where a company is financially vulnerable, it may opt against the EMV-maximizing action, even if there's a slight possibility of bankruptcy resulting from that action. Preference Theory addresses such scenarios by offering a structured method of evaluating consequences on a preference scale, which reflects the decision maker's risk attitude.
- The aim of this section is to demonstrate how Preference Theory can be applied in decision-making. The process involves extracting information from the decision maker (DM) regarding their 'certainly equivalents' (CE) for each alternative. The CE of an alternative denotes the amount the decision maker is willing to exchange for the uncertain consequences associated with that particular alternative. For instance, consider an investment option in a project with potential outcomes: (a) a net loss of Rs. 1,00,000 with a probability of 0.1, and (b) a net gain of Rs. 20,000 with a probability of 0.9. If the decision maker is risk-averse, they might not favor the small likelihood of losing Rs. 1 lakh and may prefer an alternative offering a certain amount, say Rs. 5,000, as opposed to the uncertain outcome described above (with an EMV of Rs. 8,000).
- The exclusive right belongs to a specific group of individuals, among whom our decision maker (DM) is included. In Decision Theory, if this exclusive right is permitted to be transferred to others, the DM is willing to sell it for Rs. 5,000. The discrepancy between the EMV and the CE is termed the risk premium. In this case, the CE is Rs. 5,000, resulting in a risk premium of Rs. 3,000. As the number of alternatives increases, gathering preference information in this manner becomes challenging.
- To address this issue, the Preference curve is constructed, plotting monetary value on the X-axis and preference on the Y-axis. Initially, the best and worst consequences associated with any decision are identified. Preference values of 1 and 0 are then assigned to the best and worst consequences respectively, providing two points on the Preference curve. The subsequent points are obtained using the following steps: [continue with the rephrased content]
- Let R0 represent the consequence associated with the worst decision. P(R0) denotes the preference linked with R0, set as 0.
The step for obtaining the subsequent points are given below :
- Let R0 = Consequence corresponding to worst decision.
- P(R0) = Preference corresponding to R0 = 0.
- R1= Consequence corresponding to the best decision.
- P(R1) = Preference corresponding to R1 = 1
- Step 1: We find the d.m's CE of a 50-50 chance of getting Rs. R0 or Rs. Rx. Suppose, he gives the value Rs. (CE1).
- Step 2: We find the preference corresponding to CE1 i.e.P(CE1).
Preference of an alternative is defined as the mathematical expectation of preferences corresponding to the consequences of the alternative. A preference P(x) assigned to a consequence x implies that the d.m. is indifferent to having an amount x for certain or having uncertain consequences of (a) [1-p(x)] of Rs . R0 and (b) P(x) of achieving Rs.Ri
P(CE1) = .5 x 0 + 0.5 x 1 = .5 - Step 3 Now, we ask the d.m., as to what certain amount would make him indifferent to uncertain consequences of Rs. (CE1) with probability 0.5 and Rs. Rx with probability 0.5. Say, he says Rs. (CE2).
- Step 4 We find P(CE2) = 0.5P(CE1) + 0.5P(R1) = .5 x .5 + .5 x 1 = .75
- Step 5 We continue till sufficient values of P(x) corresponding to different x are generated, and the curve of P(x) vs x can be drawn.
Once the preference curve is drawn, the preferences corresponding to each consequence of the problem can be obtained. In the same Decision Tree, the consequence can now be replaced by the preferences and the criterion of maximising expected preference be used for arriving at the decision.
Other Approaches
- In the preceding sections, we have operated under the assumption that probabilities associated with outcomes are ascertainable. However, practical scenarios often arise where making probability assessments is not feasible. In such instances, traditional criteria like EMV (Expected Monetary Value) and preference criteria become inadequate. This concluding section aims to explore alternative criteria applicable in circumstances where probabilities are unknown.
- One such criterion is the Criterion of Pessimism. As the name suggests, decision-making under this criterion is grounded in pessimism, assuming that the worst possible payoff for each alternative will materialize. A rational approach in such situations is to maximize the minimum payoff.
- Criterion of Optimism: This criterion, a variation of (a), involves not only maximizing the minimum payoff but also considering the maximum payoff. For instance, the decision-maker would evaluate both the maximum and minimum payoffs for each alternative. Then, these payoffs are weighted by the decision-maker's coefficient of optimism to determine the expected payoff for each alternative. Subsequently, the alternative with the highest expected payoff is selected. The coefficient of optimism, ranging between 0 and 1, indicates the extent to which the decision-maker favors the maximum payoff over the minimum payoff.
- Criterion of Regret: This criterion acknowledges the inherent regret in decision-making, stemming from the potential mismatch between the chosen alternative and the actual outcome. A regret of zero signifies a perfect match between the decision and the outcome. Regret can be quantified by considering a scenario with two investment proposals, where success or failure depends on economic conditions.
The consequences are delineated as follows:
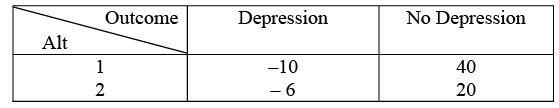
Thus, if alternative 1 is chosen, and a depression actually occurs, then there is a cause for regret, as choosing 2 would have meant a loss of only 6 (vis-a-vis 10), thus regret = 10 - 6 - 4. Similarly, if there is no depression actually, and alt. 2 has been chosen, then a regret of 40-20 = occurs. Choosing alternative1 and later finding no depression would mean zero regret. Thus, the regret matrix is found:
Now, a pessimistic stand is taken and the criterion of minimising maximum regret is used for decision. For each alternative, the maximum regret is found, and finally the alternative with minimum value of maximum regret is chosen. Thus our d.m. would have chosen alternative 1.
- Criterion of Subjectivism: Under this criterion, outcomes are considered equally probable, and the Expected Monetary Value (EMV) method is employed for decision-making. This approach is commonly referred to as the subjectivists' perspective. The aforementioned four criteria represent well-established decision-making methods. The selection of the final criterion is entirely subjective, as has become evident. Nonetheless, each criterion offers its own rationale, allowing the decision-maker to opt for any approach based on personal preference.
Conclusion
- In Decision Theory, we are equipped with the tools and methodologies to analyze decision problems when faced with uncertainty. Such problems entail various alternative courses of action, each associated with uncertain outcomes. Decision problems can manifest as single-stage or multi-stage processes. Marginal Analysis proves beneficial for single-stage problems, while the Decision Tree Approach is advantageous for multi-stage scenarios. Throughout this unit, we've delved into the application of these methods for problem-solving, primarily focusing on maximizing the Expected Monetary Value (EMV) as a criterion. EMV operates on the assumption of decision makers being risk neutral.
- Preference Theory aids in integrating the decision maker's preferences into the Decision Tree framework. We've explored how, instead of solely maximizing EMV, we can optimize expected preferences, thereby accounting for the decision maker's risk attitude. Additionally, in the unit's concluding section, we've examined alternative criteria useful for decision-making when probabilities of outcome occurrences are unknown.
FAQs on Decision Theory - Management Optional Notes for UPSC
| 1. What is decision theory? |  |
| 2. What is marginal analysis in decision theory? |  |
| 3. How does the decision tree approach work in decision theory? |  |
| 4. What is preference theory in decision theory? |  |
| 5. What are some other approaches in decision theory? |  |



















