Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Differentiation
Differentiation | Mathematics for GCSE/IGCSE - Class 10 PDF Download
What is Differentiation?
- Differentiation is a fundamental concept in Calculus, focusing on the rate of change in quantities.
- It finds extensive applications in real-world scenarios such as determining the speed of a car or the spread of a virus in a population.
- To begin to grasp differentiation, it's essential to comprehend gradients.
How are gradients related to rates of change?
- The term "gradient" typically denotes the steepness of a slope.
- For instance, lorry drivers consider the gradient of a road up a hill to gauge its steepness and plan their routes accordingly.

- On a graph, the gradient indicates the steepness of either a line or a curve.
- Essentially, it measures how quickly the y-value changes in relation to changes in the x-value.
- This measurement can be seen as the rate at which y changes.
- Therefore, the gradient describes the rate at which change occurs.
Question for DifferentiationTry yourself: What does the term "gradient" represent in the context of differentiation?View Solution
How do I find the gradient of a curve using its graph?
- For a straight line the gradient is always the same (constant)
- Recall y = mx + c, where m is the gradient
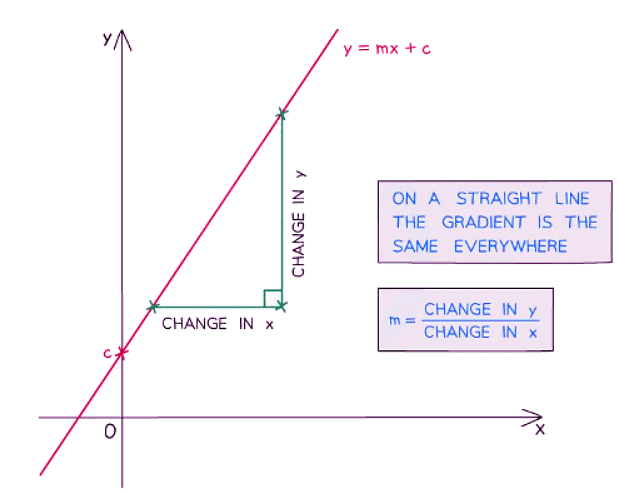
- As the value of x changes, the gradient of a curve also changes.
- At any given point on the curve, the gradient of the curve matches the gradient of the tangent line at that point.
- A tangent line is a straight line that intersects the curve at a single point.
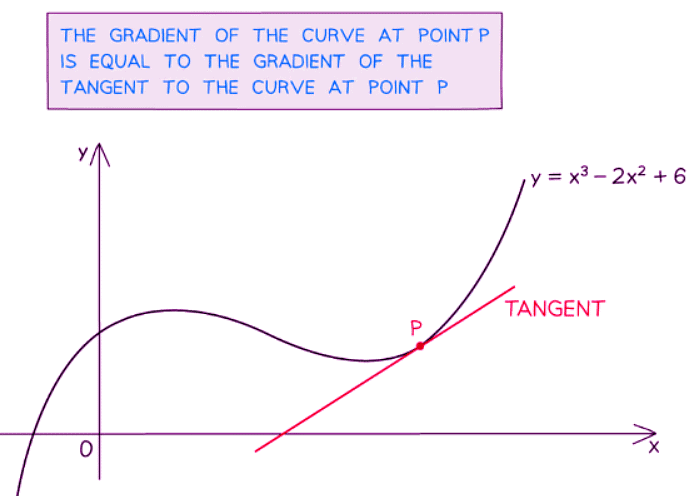
How do I find the gradient of a curve using algebra?
- Drawing tangents each time you need the gradient of a curve can be laborious.
- It would be convenient if you could obtain it using algebra instead.
- The equation of a curve can be expressed as y = f(x), where inputting x-coordinates yields y-coordinates.
- It's possible to create an algebraic function that takes x-coordinates as inputs and outputs gradients without graph sketches.
- Such a function is commonly known as the gradient function, the derivative, or the derived function.
- It's written as dx/dy, pronounced "dy by dx", or in function notation as f′(x), pronounced "f-dashed-of-x".
- To transition from
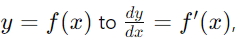 you need to perform an operation called differentiation, which converts curve equations into gradient functions.
you need to perform an operation called differentiation, which converts curve equations into gradient functions. - The primary rule for differentiation is presented.
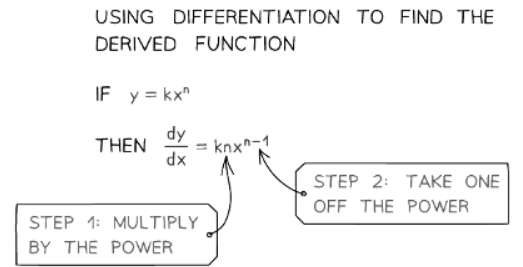
- For powers of x:
- STEP 1: Multiply the coefficient by the power.
- STEP 2: Reduce the power by 1.
- For instance, 2x6 differentiates to 12x5.
- Some notes to remember: Any constant multiplied by x differentiates to the constant itself, so 10x differentiates to 10.
- Any standalone constant differentiates to zero, so 8 differentiates to 0.
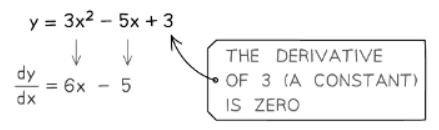
How do I use the gradient function to find gradients of curves?
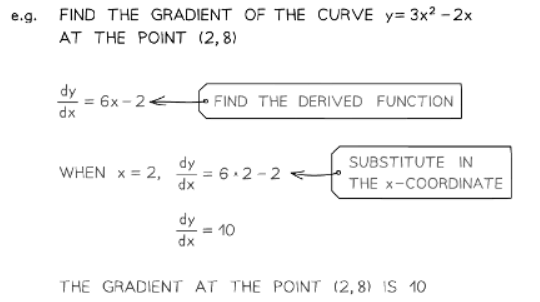
To find the x-coordinate of the point on the curve you're interested in:
- First, determine the x-coordinate of the specific point.
- Then, use differentiation to find the gradient function, represented as dx/dy.
- Substitute the x-coordinate into the gradient function to find the gradient at that point.
The document Differentiation | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
FAQs on Differentiation - Mathematics for GCSE/IGCSE - Class 10
| 1. What is differentiation? |  |
Ans. Differentiation is a mathematical process that involves finding the rate at which a function changes. It is used to calculate the gradient of a curve at a specific point, which represents the rate of change of the function at that point.
| 2. How are gradients related to rates of change? |  |
Ans. Gradients represent the rate at which a function is changing at a specific point. A positive gradient indicates an increasing function, while a negative gradient indicates a decreasing function. The steeper the gradient, the faster the rate of change.
| 3. How do I find the gradient of a curve using its graph? |  |
Ans. To find the gradient of a curve using its graph, you can draw a tangent line at a specific point on the curve. The gradient of the curve at that point is equal to the gradient of the tangent line.
| 4. How do I find the gradient of a curve using algebra? |  |
Ans. To find the gradient of a curve using algebra, you can use the derivative of the function. The derivative at a specific point gives you the gradient of the curve at that point. You can find the derivative using differentiation rules and techniques.
| 5. How do I use the gradient function to find gradients of curves? |  |
Ans. The gradient function, also known as the derivative function, gives you the gradient of a curve at any point. You can use this function to calculate the gradient at specific points or to analyze the behavior of the curve in terms of its rate of change.
Related Searches















