Dimensional Analysis & Formulas | Physics Class 11 - NEET PDF Download

Dimensional Analysis

Dimensions of a physical quantity are the power to which the fundamental quantities must be raised to represent the given physical quantity.

Dimensional AnalysisFor example, density  = (mass/volume) = mass/(length)³
or density = (mass) (length)^-3  
Thus, the dimensions of density are 1 in mass and -3 in length. The dimensions of all other fundamental quantities are zero.
For convenience, the fundamental quantities are represented by one-letter symbols. 

• Generally, mass is denoted by M, length by L, time by T, and electric current by A.
• The thermodynamic temperature, the amount of substance, and the luminous intensity are denoted by the symbols of their units K, mol, and cd respectively.
• The physical quantity that is expressed in terms of the base quantities is enclosed in square brackets.
  [sinθ] = [cosθ] = [tanθ] = [e^x] = [M⁰L⁰T⁰]

Dimensional Formula

It is an expression that shows how and which of the fundamental units are required to represent the unit of physical quantity.

For example:

By definition, Velocity is a derived quantity. We can write its dimensional formula using:

Velocity = Displacement/Time

Now, displacement is measured in Length, [L¹], and time is measured in [T¹] which are both fundamental quantities. Hence, we can represent the dimensional formula of velocity as:

[v] = [s/t] = [L/T] = [LT^-1]

Similarly, we can evaluate the dimensional formula of all physically derived quantities. The table given below shows some of the most occurring physical quantities and their dimensions.

Different quantities with units, symbols, and dimensional formulas

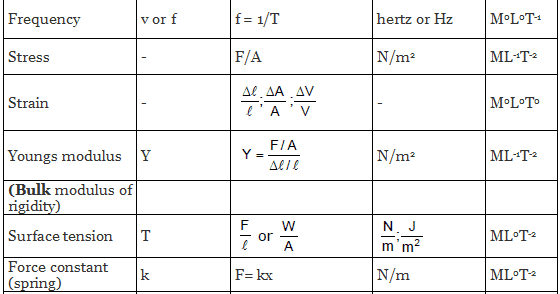
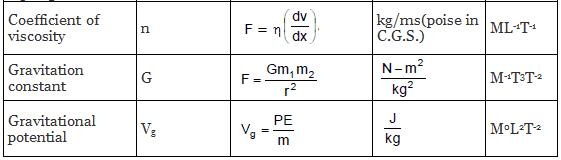
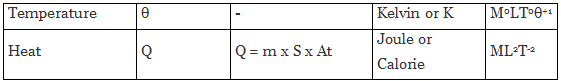
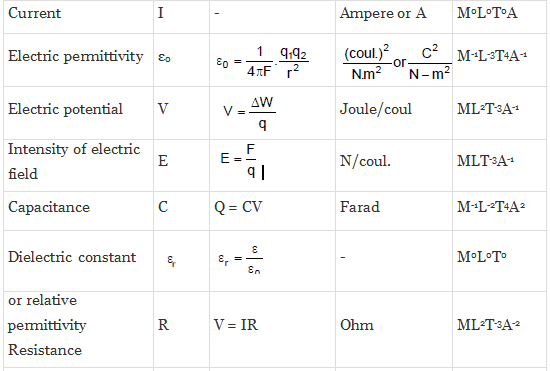
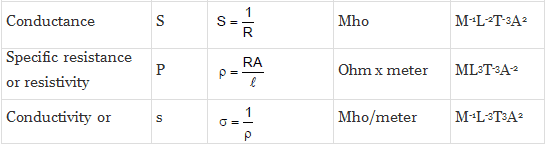
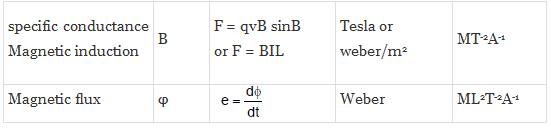
Applications of Dimensional Analysis

Conversion of units

This is based on the fact that the product of the numerical value (n) and its corresponding unit (u) is a constant, i.e.,

n[u] = constant

or n₁[u₁] = n₂ [u₂]

Suppose the dimensions of a physical quantity are a in mass, b in length, and c in time. If the fundamental units in one system are M₁, L_1, and T₁ and in the other system are M₂, L_2, and T₂ respectively. Then we can write.

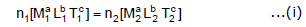Here n₁ and n₂ are the numerical values in two systems of units respectively. 

Using Eq. (i), we can convert the numerical value of a physical quantity from one system of units into the other system.

Example 1.  The value of the gravitation constant is G = 6.67 × 10^-11 Nm²/kg² in SI units. Convert it into CGS system of units. 
Solution. The dimensional formula of G is [M^-1 L³ T^-2].
Using equation number (i), i.e.,

Here, n₁ = 6.67 x 10^-11
M₁ = 1 kg, M₂ = 1 g = 10^-3 kg, L₁  = 1 m, L₂ = 1 cm = 10^-2 m, T₁ = T₂ = 1s
Substituting in the above equation, we get

or n₂ = 6.67 x 10^-8
Thus, the value of G in the CGS system of units is 6.67 x 10^-8 dyne cm²/g².

To check the dimensional correctness of a given physical equation

• Every physical equation should be dimensionally balanced. This is called the 'Principle of Homogeneity'. 
• The dimensions of each term on both sides of an equation must be the same. On this basis, we can judge whether a given equation is correct or not. However, a dimensionally correct equation may or may not be physically correct.

Example 2. Show that the expression of the time period T of a simple pendulum of length l given by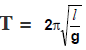

is dimensionally correct.  
Solution.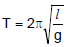 

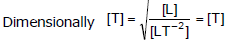As in the above equation, the dimensions of both sides are the same. The given formula is dimensionally correct.

Principle of Homogeneity of Dimensions

This principle states that the dimensions of all the terms in a physical expression should be the same. For example, in the physical expression s = ut + 1/2 at²,  the dimensions of s, ut, and 1/2 at² all are the same.

Note: The physical quantities separated by the symbols +, -, =, >, <, etc., have the same dimensions.

Example 3. The velocity v of a particle depends upon the time t according to the equation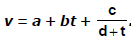 
. 
Write the dimensions of a, b, c, and d. 
Solution.
From the principle of homogeneity

To establish the relation among various physical quantities

If we know the factors on which a given physical quantity may depend, we can find a formula relating the quantity to those factors. Let us take an example.

Example.4. The frequency (f) of a stretched string depends upon the tension F (dimensions of force), length l of the string, and the mass per unit length m of string. Derive the formula for frequency. 
Solution. Suppose, that the frequency f depends on the tension raised to the power a, length raised to the power b, and mass per unit length raised to the power c. Then.
f ∝ [F]^a[l]^b[μ]^c
or f = k[F]^a[l]^b[μ]^c
Here, k is a dimensionless constant. Thus,
[f] = [F]⁰[l]^b[μ]^c
or [M⁰L⁰T^-1] = [MLT^-2]^a[L]^b[ML^-1]^c
or [M⁰L⁰T^-1] = [M^a+c L^a+b-c T^-2a]
For dimensional balance, the dimensions on both sides should be the same.
Thus,    a + c = 0    ...(ii)
a + b - c = 0    ...(iii)
and    - 2a = - 1    ...(iv)
Solving these three equations, we get
a = 1/2, c = (-1/2) and b = -1
Substituting these values in Eq. (i), we get
f = k(F)^1/2(l)^-1(μ)^-1/2
or
Experimentally, the value of k is found to be 1/2

Limitations of Dimensional Analysi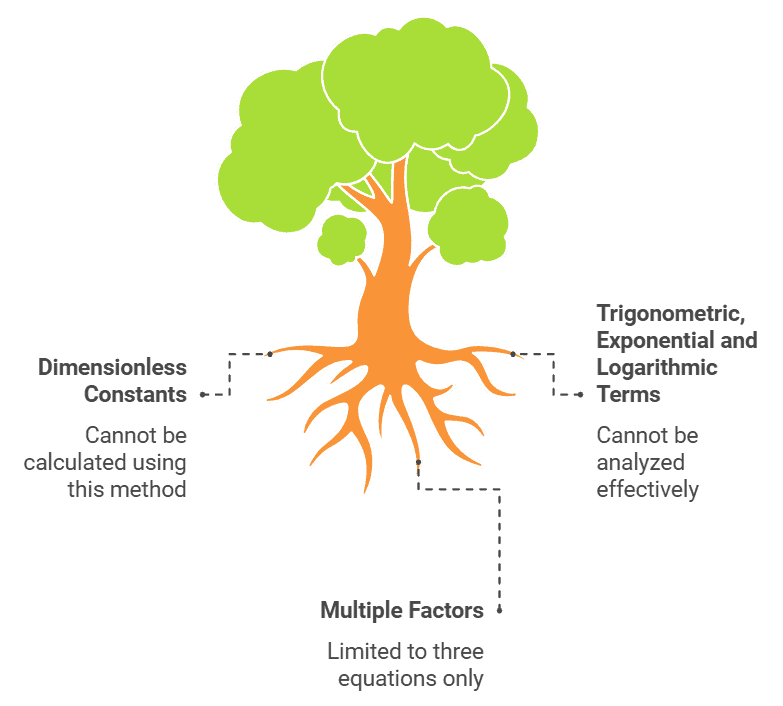s 

The method of dimensions has the following limitations:

(a) By this method the value of dimensionless constant can not be calculated.

(b) By this method the equation containing trigonometrical, exponential, and logarithmic terms cannot be analyzed.

(c) If a physical quantity depends on more than three factors, then a relation among them cannot be established because we can have only three equations by equalizing the powers of M, L, and T.