Dual Nature of Matter & Heisenberg's Uncertainty Principle | Chemistry Class 11 - NEET PDF Download
DeBroglie's Hypothesis:
- DeBroglie proposed that like light, electrons possess a dual nature i.e. behave both as material particles and as waves.
- The concept of the dual character of metal evolved a wave mechanical theory of atoms according to which electrons, protons, and even atoms possess wave properties when moving.
 Dual Nature of Matter
Dual Nature of Matter
Derivation of De Broglie's Relationship :
For a photon,
...(i)
...(ii)
He concluded that electromagnetic radiation has some associated mass or associated momentum, in the same way every moving particle of mass `m' and velocity `v' is associated with waves and these associated waves are known as matter waves or De Broglie's waves.
Experimental verification of De Broglie's hypothesis: Given by Davission and Germer.
They observed that a beam of electrons is diffracted by nickel crystal just like the x-rays. Moreover, the wavelength of the electrons determined by the diffraction experiments are equal to the values calculated from De Broglie's relationship.
Derivation of Bohr's postulate of quantization of angular momentum from De Broglie's Equations-
According to De Broglie, moving electrons associated with waves must be completely in phase, and therefore, only those orbits are possible where the circumference of the orbit is an integral multiple of λ i.e.
, where n is the no. of waves
From the above expression, it can be commented that
no of waves in a shell waves = shell no.
 Quantization of Angular Momentum of Electron
Quantization of Angular Momentum of Electron
Calculation of De Broglie wavelength if K.E. of the particle is E
2E = mv2; 2mE = m2 v2 = p2
If a charged particle at rest (having charge `q') is accelerated by potential difference'V' volt then,
,
(Only for electrons).
Ex. Calculate λdB of an electron having K.E. 3 eV.
Sol.
Heisenberg Uncertainty Principle:
- The position and momentum of a particle cannot be simultaneously measured with arbitrarily high precision.
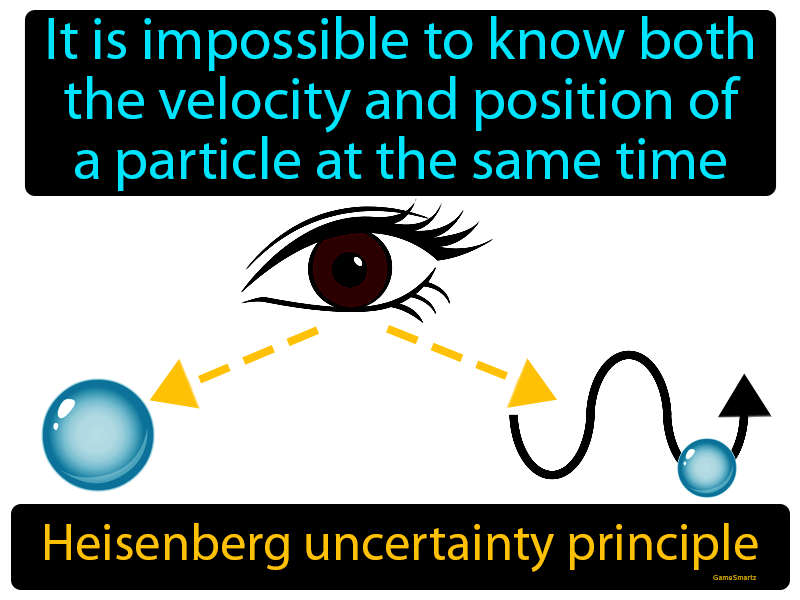 Heisenberg's Uncertainty Principle
Heisenberg's Uncertainty Principle
- There is a minimum for the product of the uncertainties of these two measurements.
- There is likewise a minimum for the product of the uncertainties of the energy and time.
- The uncertainty principle contains implications about the energy that would be required to contain a particle within a given volume.
- The energy required to contain particles comes from the fundamental forces, and in particular, the electromagnetic force provides the attraction necessary to contain electrons within the atom, and the strong nuclear force provides the attraction necessary to contain particles within the nucleus.
- But Planck's constant, appearing in the uncertainty principle, determines the size of the confinement that can be produced by these forces.
- Another way of saying it is that the strengths of the nuclear and electromagnetic forces along with the constraint embodied in the value of Planck's constant determine the scales of the atom and the nucleus.
Example of Heisenberg Uncertainty Principle
- To grasp the uncertainty principle, let's consider a practical example. Imagine you're tasked with measuring the thickness of a sheet of paper using an unmarked meterstick. It's clear that such measurements would be imprecise and meaningless. For accurate results, you'd need a measuring tool with units smaller than the thickness of the paper.
- Similarly, when trying to pinpoint the position of an electron, we face a challenge. Electrons are incredibly tiny, often considered point charges without a measurable size. To observe an electron, we typically use "light" or electromagnetic radiation. However, this light must have a wavelength smaller than the dimensions of an electron. If we illuminate the electron with light that has too large a wavelength, it would alter the electron's energy during collisions.
- In essence, while we could calculate the position of the electron through this process, we would end up knowing very little about its velocity after the collision. This illustrates the fundamental idea behind the uncertainty principle.
Significance of Heisenberg Uncertainty Principle
- One of the profound implications of the Heisenberg Uncertainty Principle is that it eliminates the possibility of defining precise paths or trajectories for electrons and similar particles.
- In classical physics, the trajectory of an object is determined by its position and velocity at different moments. If we know the location, velocity, and forces acting on an object at a particular instant, we can predict its future position. Therefore, the position and velocity of an object fix its trajectory.
- However, for sub-atomic particles like electrons, it is impossible to simultaneously determine their position and velocity at any given moment with arbitrary precision. This inherent limitation means we cannot accurately describe the trajectory of an electron.
- It's crucial to understand that the impact of the Heisenberg Uncertainty Principle is significant for the motion of microscopic objects, such as electrons, but negligible for macroscopic objects.
|
114 videos|263 docs|74 tests
|
FAQs on Dual Nature of Matter & Heisenberg's Uncertainty Principle - Chemistry Class 11 - NEET
| 1. What is De Broglie's hypothesis? |  |
| 2. How is De Broglie's relationship derived? |  |
| 3. What is the Heisenberg uncertainty principle? |  |
| 4. How does the dual nature of matter relate to the Heisenberg uncertainty principle? |  |
| 5. What are some applications of the Heisenberg uncertainty principle? |  |






















