Dual Nature Of Radiation And Matter | Physics Class 12 - NEET PDF Download
What is Electron Emission?
- When light is incident on a metal surface it was observed that electrons are ejected from a metal surface some times even when incredibly dim light such as that from stars and distant galaxies incident on it and some time electrons does not come out from the metal surface even high energetic or high-intensity light falling on the metal surface.
- This shows that the electron emission from a metal surface does not depend on the intensity of incident light but it basically depends on the energy of the incident.
- Photons no matters in the number of photons are very less in dim light, photoelectric effect can be seen.
- During the phenomenon of the photoelectric effect, one incident photon on the metal surface can eject at most only one electron.
- A photon is an energy packet that is fully absorbed not partially. Thus one photon can not be absorbed by more than one electron.
- The minimum amount of energy of photon required to eject an electron out of a metal surface is called work function. It is denoted by φ.
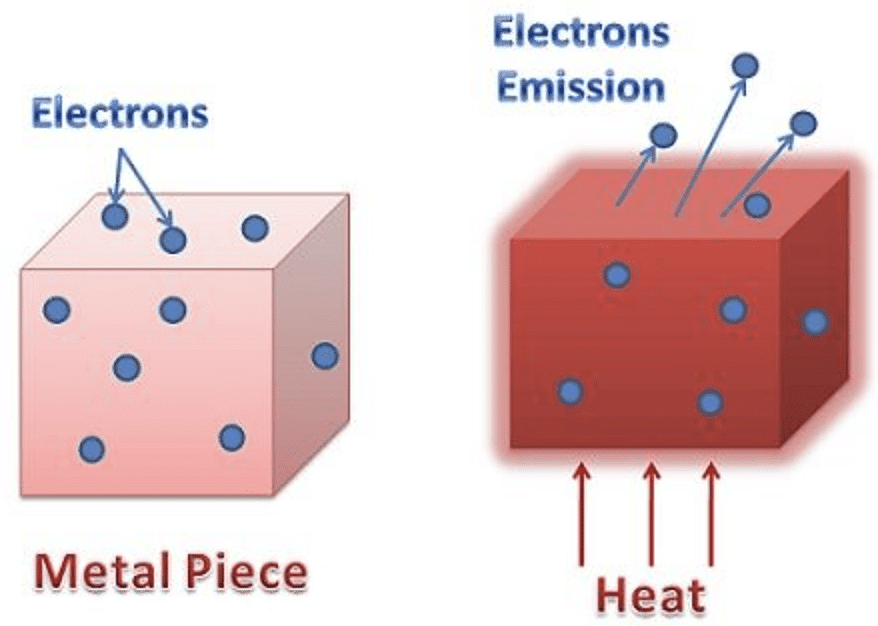
 Electron Emission from metal
Electron Emission from metal
However, the surface barrier can be broken by providing a certain minimum amount of energy to the free electrons which increases their kinetic energy and consequently help them escape the metal surface.
This minimum amount of energy is known as the work function of the metal. And when the work function is provided to the metal, the consequent liberation of electrons from the metal surface is known as electron emission.
The work function of a metal depends on:
- The electron emission from metal only depends on the work function or energy of one photon.
- But how many electrons come out from the metal depends on the intensity of the falling light on the energy of the light.
- The energy of a photon incident on metal will not necessarily cause emission of an electron even if its energy is more than the work function.
- The electron after absorption may be involved in many other processes like collision etc in which it can lose energy.
- Hence the ratio of the number of electrons emitted to the number of photons incident on the metal surface is less than unity.
Types of Electron Emission
The electron emission is possible only if sufficient energy (equal to the work function of the metal) is supplied to the metal in the form of heat energy, light energy, etc. Depending on the source of energy, electron emission can be of the following types:
- Thermionic Emission: In this type, the metal is heated to a sufficient temperature to enable the free electrons to come out of its surface.

- Field Emission: In this type, a very strong electric field is applied to the metal which pulls the electrons out of the surface due to the attraction of the positive field.

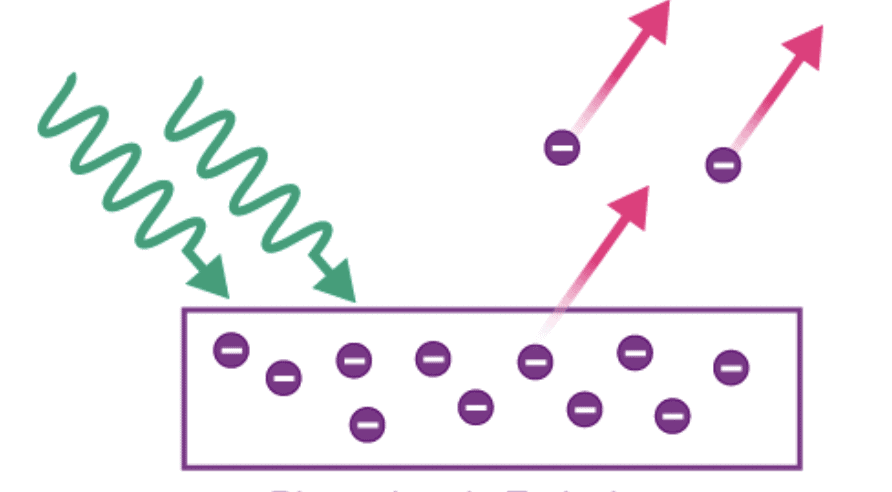
- Photoelectric Emission: In this type, the light of a certain frequency is made to fall on the metal surface which leads to the emission of electrons.

Photoelectric Effect
The photoelectric effect refers to the release of electrons from a metal surface when it is exposed to light or other electromagnetic radiation of a suitable frequency.
- These released electrons are called photoelectrons, and the resulting current is known as photoelectric current.
- Certain metals, such as alkali metals like lithium and sodium, exhibit the photoelectric effect with visible light, whereas metals like zinc and cadmium require ultraviolet light to show this effect.
Note: Non-metals, liquids, and gases can also show the photoelectric effect, although to a limited extent.
Hertz’s Observations
In 1887, Heinrich Hertz observed the photoelectric effect while conducting experiments on electromagnetic waves. He noticed that when ultraviolet light from an arc lamp was directed onto a metal emitter plate, it increased the high-voltage sparks across a detector loop.
This phenomenon was explained as follows:
When radiation of a suitable frequency falls on a metal surface, electrons near the surface absorb enough energy from the light to overcome the attraction of positive ions within the metal. This energy allows the electrons to escape from the surface into the surrounding space.
Hallwachs’ and Lenard’s Observations
- Between 1886 and 1902, Wilhelm Hallwachs and Philipp Lenard conducted detailed studies of the photoelectric effect.
- Lenard found that, in an evacuated tube with two metal plates, no current flowed if a potential difference was applied between the plates.
- However, if one plate (the emitter plate) was exposed to ultraviolet light, a current began to flow.
- When the ultraviolet light was removed, the current stopped. This demonstrated that light on the emitter plate could cause current to flow in the circuit.
- Hallwachs concluded that ultraviolet light causes negatively charged particles to be emitted from the metal surface, which was later understood to be electrons.
- These electrons are then pushed toward the collector plate by the applied electric field.
- Hallwachs and Lenard also observed that electrons were only emitted when the frequency of the incident light exceeded a certain minimum value, called the threshold frequency, which depends on the nature of the metal surface.
Experimental Study of Photoelectric Effect
- The setup for studying the photoelectric effect includes an evacuated glass or quartz tube containing a photosensitive plate C (referred to as the emitter) and a metal plate A (referred to as the collector).
- A transparent quartz window is fitted to the glass tube, allowing ultraviolet light to enter and irradiate the photosensitive plate C.
 Experimental arrangement for the study of photoelectric effect
Experimental arrangement for the study of photoelectric effect
- In this setup, electrons are emitted from the plate C when exposed to ultraviolet radiation and are collected by plate A.
- When the collector plate A is positively charged relative to the emitter plate C, it attracts the emitted electrons, creating a flow of electric current, known as the photoelectric current, in the circuit.
- The potential difference between the emitter and collector plates is measured with a voltmeter (V), while the photocurrent generated in the circuit is measured with a microammeter (μA).
- This experimental arrangement allows for the investigation of how photocurrent varies with the intensity and frequency of the incident radiation, as well as with the potential difference between plates A and C.
Effect of Intensity of Light on Photoelectric Current
At a fixed frequency of incident light and accelerating potential, the photoelectric current increases linearly as the intensity of the light increases. This relationship suggests that the photoelectric current is directly proportional to the number of photoelectrons emitted per second, which in turn depends on the intensity of the incident light.
Effect of Potential on Photoelectric Current
With a constant frequency and intensity of incident light, the photoelectric current increases as the potential applied to the collector becomes more positive, as illustrated in the graph.
 Variation of photoelectric current versus potential for different intensities but constant frequencyFrom the graph, we can observe:
Variation of photoelectric current versus potential for different intensities but constant frequencyFrom the graph, we can observe:
Saturation Current: When the accelerating potential reaches a certain value, all emitted photoelectrons are able to reach the collector plate, resulting in a maximum, constant photocurrent known as the saturation current.
Current without Accelerating Potential: When the potential is reduced to zero, the current decreases but does not reach zero, indicating that even without accelerating potential, some photoelectrons reach the collector plate due to their inherent kinetic energy.
Stopping Potential (Cut-Off Potential): For a specific frequency of incident light, applying a minimum negative potential V0 to the collector plate causes the photoelectric current to drop to zero. This minimum negative potential, where even the most energetic photoelectrons cannot reach the collector, is called the stopping potential or cut-off potential.
The stopping potential is directly related to the maximum kinetic energy Kmax of the photoelectrons, as given by:

Where, m is the mass of photoelectron and vmax is the maximum velocity of emitted photoelectron.
Effect of Frequency of Incident Radiation on Stopping Potential
When radiation of different frequencies (but the same intensity) is used, the photoelectric current varies with the potential difference between the plates, as shown in the graph.
 Variation of photoelectric current versus potential for different frequencies but constant intensity of incident radiation
Variation of photoelectric current versus potential for different frequencies but constant intensity of incident radiation
From the graph, we observe:
Stopping Potential and Frequency: The stopping potential varies with the frequency of the radiation but the saturation current remains constant for a given intensity.
Higher Frequency and Higher Stopping Potential: The stopping potential is more negative for higher-frequency radiation, indicating that the kinetic energy of emitted electrons depends on the radiation frequency. Higher frequencies result in higher kinetic energies for the photoelectrons, requiring a greater stopping potential to halt them.
Saturation Current and Intensity: The saturation current depends on the intensity of the radiation but is independent of the frequency.
If we plot stopping potential against the frequency of incident radiation for two different metals, we get a linear graph for each metal. This graph shows:
 Variation of stopping potential versus frequency of incident radiation
Variation of stopping potential versus frequency of incident radiation
Linear Relationship: For a given photosensitive material, the stopping potential V0 varies linearly with the frequency of incident radiation.
Threshold Frequency: There is a minimum cut-off frequency ν0 below which no photoelectric emission occurs, regardless of intensity. This cut-off frequency is called the threshold frequency.
Note: The minimum frequency required to emit photoelectrons is known as the threshold frequency or cut-off frequency and is a characteristic of each material. Below this frequency, no photoelectric emission takes place, even if the light intensity is high. If the frequency is above the threshold, photoemission occurs immediately (within 10−9 seconds or less), even with low-intensity light.
Example 1. The photoelectric threshold of the photoelectric effect of a certain metal is 2750 Å. Find
(i) The work function of emission of an electron from this metal,
(ii) Maximum kinetic energy of these electrons,
(iii) The maximum velocity of the electrons ejected from the metal by light with a wavelength of 1800 Å.
Sol. (i) Given that the threshold wavelength of a metal is λth = 2750 Å. Thus work function of metal can be given as φ = 
(ii) The energy of an incident photon of wavelength 1800 Å on metal in eV is  = 6.9 eV
= 6.9 eV
Thus maximum kinetic energy of ejected electrons is
KEmax = E – φ = 6.9 - 4.52 eV = 2.38 eV
(iii) If the maximum speed of ejected electrons is vmax then we have  = 2.38 eV
= 2.38 eV
or  = 9.15 X 105 m / s
= 9.15 X 105 m / s
Example 2. Light quanta with an energy of 4.9 eV eject photoelectrons from metal with work function of 4.5 eV. Find the maximum impulse transmitted to the surface of the metal when each electron flies out.
Sol. According to Einstein's photoelectric equation
E =  = hv - φ = 4.9 - 4.5 = 0.4 eV
= hv - φ = 4.9 - 4.5 = 0.4 eV
If E be the energy of each ejected photoelectron momentum of electrons is p = 
We know that change of momentum is impulse. Here the whole momentum of the electron is gained when it is ejected out thus impulse on the surface is Impulse = 
Substituting the values, we get
Maximum impulse =  = 3.45 X10 -25 kg m / sec
= 3.45 X10 -25 kg m / sec
Example 3. In an experiment tungsten cathode which has a threshold of 2300 Å is irradiated by the ultraviolet light of wavelength 1800 Å. Calculate
(i) Maximum energy of emitted photoelectron and
(ii) Work function for tungsten
(Mention both the results in electron-volts)
Given Plank's constant h = 6.6 X 10 -34 joule-sec, 1 eV = 1.6 X 10 -19joule and velocity of light c = 3 X 108 m/sec
Sol. The work function of tungsten cathode is  = 5.4 eV
= 5.4 eV
The energy in eV of incident photons is

The maximum kinetic energy of ejected electrons can be given as
KEmax = E - φ = 6.9 - 5.4 eV = 1.5 eV
Example 4. Light of wavelength 1800 Å ejects photoelectrons from a plate of a metal whose work functions is 2 eV. If a uniform magnetic field of  tesla is applied parallel to the plate, what would be the radius of the path followed by electrons ejected normally from the plate with maximum energy.
tesla is applied parallel to the plate, what would be the radius of the path followed by electrons ejected normally from the plate with maximum energy.
Sol. Energy of incident photons in eV is given as

As work function of metal is 2 eV, the maximum kinetic energy of ejected electrons is KEmax = E - φ = 6.9 – eV = 4.9 eV
If vmax be the speed of fasted electrons then we have  = 4.9 X1.6 X10 -19 joule
= 4.9 X1.6 X10 -19 joule
or  = 1.31 X 106 m/s
= 1.31 X 106 m/s
When an electron with this speed enters a uniform magnetic field normally it follows a circular path whose radius can be given by


or  or r = 0.149 m
or r = 0.149 m
Laws of Photoelectric Emission
Proportionality with Intensity: For a given material and a fixed frequency of incident radiation, the photoelectric current (or the rate at which photoelectrons are emitted) is directly proportional to the intensity of the incoming light.
Saturation Current and Stopping Potential: For a specific material and frequency of incident light, the saturation current is proportional to the intensity of the radiation. However, the stopping potential remains unaffected by the light's intensity.
Threshold Frequency: For each material, there is a minimum frequency of incident radiation below which no photoelectrons are emitted, regardless of the intensity. This minimum frequency is known as the threshold frequency. Above this frequency, the maximum kinetic energy of the photoelectrons (or the stopping potential) depends only on the frequency (or wavelength) of the light, not on its intensity.
Instantaneous Emission: Photoelectric emission occurs almost instantaneously. The time delay between the arrival of radiation and the emission of photoelectrons is extremely brief, less than 10−9 seconds.
Photoelectric Effect And Wave Theory of Light
- Light has always fascinated thinkers and scientists.
- It wasn't until the late 17th century that scientists started to understand the properties of light.
- Sir Isaac Newton suggested that light consists of tiny particles called photons.
- In contrast, Christian Huygens believed that light behaves like waves that move at right angles to their direction.
- In 1678, Huygens introduced the idea that every point where a light disturbance occurs acts as a source of a new spherical wave.
- The overall shape of this new wave is determined by adding together all the secondary waves created by the disturbance.
- This concept is known as Huygens' Principle.
- Using this principle, Huygens successfully derived the laws of reflection and refraction of light.
- He also explained how light travels in straight lines and in spherical patterns.
- However, Huygens struggled to explain the diffraction effects of light.
- In 1803, Thomas Young conducted an experiment on light interference that confirmed Huygens' wave theory.
- Later, in 1815, Fresnel provided mathematical equations that supported Young's findings.
- Max Planck introduced the idea that light is made up of small energy packets called light quanta, which depend on the light's frequency and speed.
- Then, in 1905, Albert Einstein suggested that light has both particle and wave characteristics.
- He claimed that light is composed of tiny particles called photons.
- The field of quantum mechanics later confirmed this dual nature of light.

Einstein’s Photoelectric Equation
Energy Quantum of Radiation

Photoelectric Effect
The photoelectric effect is a phenomenon where electrons are emitted from the metal surface when the light of sufficient frequency is incident upon. The concept of the photoelectric effect was first documented in 1887 by Heinrich Hertz and later by Lenard in 1902. But both the observations of the photoelectric effect could not be explained by Maxwell’s electromagnetic wave theory of light. Hertz (who had proved the wave theory) himself did not pursue the matter as he felt sure that it could be explained by the wave theory. However, the concept failed in the following accounts:
- According to the wave theory, energy is uniformly distributed across the wavefront and is dependent only on the intensity of the beam. This implies that the kinetic energy of electrons increases with light intensity. However, the kinetic energy was independent of light intensity.
- Wave theory says that light of any frequency should be capable of ejecting electrons. But electron emission occurred only for frequencies larger than a threshold frequency (ν0).
- Since energy is dependent on intensity according to wave theory, the low-intensity light should emit electrons after some time so that the electrons can acquire sufficient energy to get emitted. However, electron emission was spontaneous no matter how small the intensity of light.
Einstein’s Explanation of Photoelectric Effect
- Einstein resolved this problem using Planck’s revolutionary idea that light was a particle.
- The energy carried by each particle of light (called quanta or photon) is dependent on the light’s frequency (ν) as shown:
E = hν
where h = Planck’s constant = 6.6261 × 10-34 Js. - Since light is bundled up into photons, Einstein theorized that when a photon falls on the surface of a metal, the entire photon’s energy is transferred to the electron.
- A part of this energy is used to remove the electron from the metal atom’s grasp and the rest is given to the ejected electron as kinetic energy.
- Electrons emitted from underneath the metal surface lose some kinetic energy during the collision. But the surface electrons carry all the kinetic energy imparted by the photon and have the maximum kinetic energy.
- We can write this mathematically as:
Energy of photon = energy required to eject an electron (work function) + Maximum kinetic energy of the electron
E = W + K.E.
hv = W + K.E.
K.E. = hv – w - At the threshold frequency, ν0 electrons are just ejected and do not have any kinetic energy. Below this frequency, there is no electron emission. Thus, the energy of a photon with this frequency must be the work function of the metal.
w = hv0 - Thus, Maximum kinetic energy equation becomes:
KE = 1 / 2mv2max = hv – hv0
1 / 2mv2max = h(v − v0) - Vmax is the maximum kinetic energy of the electron. It is calculated experimentally using the stopping potential.
Stopping potential = ev0 = 1 / 2mv2max - Thus, Einstein explained the Photoelectric effect by using the particle nature of light.
Example 5. The work function of caesium is 2.14 eV. Calculate
(i) the threshold frequency for caesium and
(ii) the wavelength of the incident light, if the photocurrent is brought to zero by a stopping potential of 0.60 V. Given, h=6.63×10−34J-s.

Verification of Laws of Photoelectric Emission Based on Einstein’s Photoelectric Equation
Einstein’s photoelectric equation is: 
This equation effectively explains the laws of photoelectric emission:
Threshold Frequency Requirement: If the frequency ν is less than the threshold frequency ν0, then
 would be negative, which is impossible. Therefore, for photoelectric emission to occur, the frequency ν must be greater than ν0.
would be negative, which is impossible. Therefore, for photoelectric emission to occur, the frequency ν must be greater than ν0.Proportionality with Intensity: Since each photon causes the release of one electron, the number of emitted photoelectrons per second is directly proportional to the intensity of the incident light.
Kinetic Energy and Frequency: The maximum kinetic energy
 is directly proportional to the frequency ν, as h and ν0 are constants. This shows that the kinetic energy of the photoelectrons increases with the frequency of the incident light.
is directly proportional to the frequency ν, as h and ν0 are constants. This shows that the kinetic energy of the photoelectrons increases with the frequency of the incident light.Instantaneous Emission: Photoelectric emission is the result of elastic collisions between photons and electrons, meaning there is no significant time delay between the photon hitting the surface and the emission of a photoelectron.
Graphs Related to Photoelectric Effect From Einstein's Photoelectric Equation
The important graphs related to the photoelectric effect are as follows:











Particle Nature of Light: The Photon
The emission of free electrons from a metal surface when the light is shone on it, it is called the photoemission or the photoelectric effect.
- This effect led to the conclusion that light is made up of packets or quantum of energy.
- Now the question was whether the light quantum theory was indicative of the particle nature of light.
- Einstein already associated the light quantum with momentum.
- This strongly supported the particle nature of light and these particles were named photons.
- Thus, the wave-particle duality of light came into the picture.
 Photoelectric Emission
Photoelectric Emission
Some points to be kept in mind are:
- A photon is an elementary particle. It is a quantum of light.
- Energy of a photon is given by E = hν. Its momentum is p = hν / c and speed is c, which is the speed of light.
- Irrespective of the intensity of radiation, every photon of a frequency v has the same momentum p = h / νc and energy E = hν.
- The increase in the intensity of light only increases the number of photons crossing an area per unit time. It does not affect the energy of the radiation.
- A photon remains unaffected by electric and magnetic fields. It is electrically neutral.
- A photon has a zero mass, i.e. it is massless.
- It is a stable particle.
- Photons can be created or destroyed when radiation is emitted or absorbed.
- The total energy and momentum are conserved during a photon-electron collision.
- A photon cannot decay on its own.
- The energy of a photon can be transferred during an interaction with other particles.
- A photon is a spin-1 particle, unlike electrons which are ½ spin. It’s spin axis is parallel to the direction of travel. It is this property of photons which supports the polarization of light.
Wave Nature of Matter
- The wave nature of matter is a very strange idea in Physics.
- You have seen examples of both the particle nature and wave nature of light.
- The photoelectric effect, explained by Albert Einstein, demonstrates how electrons and photons behave like particles, similar to how a billiard ball acts.
- However, you likely remember the diffraction experiment and interference rings, which show the wave nature of light, much like how two ripples on a pond interact with each other.
- This concept is quite fascinating and even relates to how we see!
- The way light is gathered and focused by the lens of the eye aligns with the wave nature of light.
- Yet, when light is absorbed by the rods and cones in our retina, it reflects the particle nature of light.
- While we were still trying to grasp this mystery, Louis de Broglie introduced his de Broglie Relation, adding even more complexity to the topic.
De Broglie’s Equation
- De Broglie’s hypothesis stated that there is symmetry in nature and that if light and radiation behave as both particles and waves, matter too will have both the particle and wave nature.
- λ = h / p = h / mv
- Through the de Broglie’s relationship, we now had a wave theory of matter. The ‘Lambda’ here represents the wavelength of the particle and p represents the momentum of the particle.
- The significance of the de Broglie relationship is that it proves mathematically that matter can behave as a wave. In layman terms, the de Broglie equation says that every moving particle – microscopic or macroscopic – has its own wavelength.
- For macroscopic objects, the wave nature of matter is observable.
- For larger objects, the wavelength gets smaller with the increasing size of the object, quickly becoming so small as to become unnoticeable which is why macroscopic objects in real life don’t show wave-like properties.
- Even the cricket ball you throw has a wavelength that is too small for you to observe. The wavelength and the momentum in the equation are connected by the Plank’s constant.
Heisenberg’s Uncertainty
- The Davisson-Germer experiment proved beyond doubt the wave nature of matter by diffracting electrons through a crystal.
- In 1929, de Broglie was awarded the Nobel Prize for his matter wave theory and for opening up a whole new field of Quantum Physics.
- The matter-wave theory was gracefully incorporated by Heisenberg’s Uncertainty Principle.
- The Uncertainty Principle states that for an electron or any other particle, both the momentum and position cannot be known accurately at the same time.
- There is always some uncertainty with either the position ‘delta x’ or with the momentum, ‘delta p’.
- Heisenberg’s Uncertainty Equation:
σxσp ≤ h / 2
Say you measure the momentum of the particle accurately so that ‘delta p’ is zero. To satisfy the equation above, the uncertainty in the position of the particle, ‘delta x’ has to be infinite.
From de Broglie’s equation, we know that a particle with a definite momentum has a definite wavelength ‘Lambda’. A definite wavelength extends all over space all the way to infinity. By Born’s Probability Interpretation, this means that the particle is not localized in space and therefore the uncertainty of position becomes infinite.
In real life though, the wavelengths have a finite boundary and are not infinite and thus both the position and momentum uncertainties have a finite value. De Broglie’s equation and Heisenberg’s Uncertainty Principle are apples of the same tree.
|
97 videos|336 docs|104 tests
|
FAQs on Dual Nature Of Radiation And Matter - Physics Class 12 - NEET
| 1. What is electron emission and why is it important in physics? |  |
| 2. What are the main types of electron emission? |  |
| 3. What is the photoelectric effect and how does it demonstrate the particle nature of light? |  |
| 4. What are the laws of photoelectric emission? |  |
| 5. What is Einstein’s photoelectric equation and what does it signify about the dual nature of radiation? |  |

|
Explore Courses for NEET exam
|

|


 would be negative, which is impossible. Therefore, for photoelectric emission to occur, the frequency ν must be greater than ν0.
would be negative, which is impossible. Therefore, for photoelectric emission to occur, the frequency ν must be greater than ν0. is directly proportional to the frequency ν, as h and ν0 are constants. This shows that the kinetic energy of the photoelectrons increases with the frequency of the incident light.
is directly proportional to the frequency ν, as h and ν0 are constants. This shows that the kinetic energy of the photoelectrons increases with the frequency of the incident light.

















