DC Pandey Solutions: Elasticity | Physics Class 11 - NEET PDF Download
Introductory Exercise 12.1
Ques 1: Two wires A and B of same dimensions are stretched by same amount of force. Young's modulus of A is twice that of B. Which wire will get more elongation?
Sol:
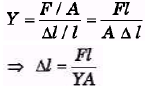
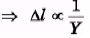 as Young's modulus of A is twice of B, so elongation of A will be half of B.
as Young's modulus of A is twice of B, so elongation of A will be half of B.
Ques 2: A rod 100 cm long and of 2 cm × 2 cm cross-sect ion is subjected to a pull of 1000 kg force. If the modulus of elasticity of the material is 2.0 × 106 kg/cm2, determine the elongation of the rod.
Sol:
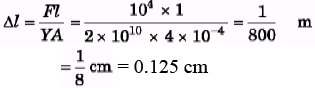
Ques 3: A cast iron column has internal diameter of 200 mm. What should be the minimum external diameter so that it may carry a load of 1.6 MN without the stress exceeding 90 N/mm2?
Sol:
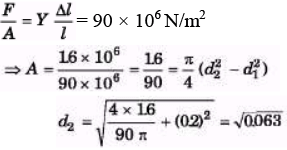
= 0250 = 250 mm
EXERCISES
For JEE Main
Subjective Questions
Ques 1: A cylindrical steel wire of 3 m length is to stretch no more than 0.2 cm when a tensile force of 400 N is applied to each end of the wire. What minimum diameter is required for the wire?
Ysteel =2.1 × 1011 N/m2
Sol:
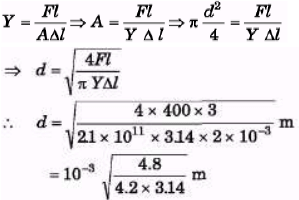
= 1.9 × 10-3 m = 1.9 mm
Ques 2: The elastic limit of a steel cable is 3.0 × 108 N/m2 and the cross-section area is 4cm2. Find the maximum upward acceleration that can be given to a 900 kg elevator supported by the cable if the stress is not to exceed one-third of the elastic limit.
Sol: 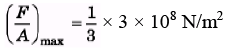
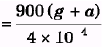
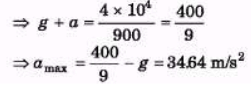
Ques 3: If the elastic limit of copper is 1.5 x 108N/m2, determine the minimum diameter a copper wire can have under a load of 10.0 kg, if its elastic limit is not to be exceeded.
Sol:
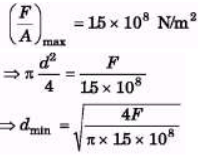
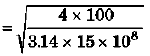
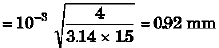
Ques 4: Find the increment in the length of a steel wire of length 5 m and radius 6 mm under its own weight. Density of steel = 8000 kg/m3 and Young's modulus of steel = 2 x 1011 N/m2. What is the energy stored in the wire? (Take g = 9.8m/s2)
Sol: 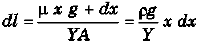
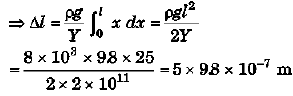
= 49 × 10-6 m
Ques 5: Two wires shown in figure are made of the same material which has a breaking stress of 8 × 108 N/m2. The area of cross-section of the upper wire is 0.006 cm2 and that of the lower wire is 0.003 cm . The mass m1 = 10 kg, m2 = 20 kg and the hanger is light. Find the maximum load that can be put on the hanger without breaking a wire. Which wire will break first if the load is increased? (Take g = 10 m/s2)
Sol: 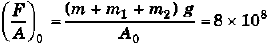
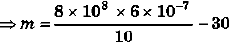
= 48 - 30 = 18 kg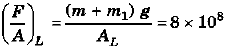
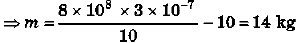
So, lower wire will break if m > 14 kg. i.e., maximum load which can be put on hanger without breaking wire is 14 kg.
Ques 6: A steel wire and a copper wire of equal length and equal cross-sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of:
(a) the stresses developed in the two wires,
(b) the strains developed. (Y of steel =2 × 1011 N/m2 and T of copper = 1.3 × 1011 N/m2)
Sol: F/A is same as both have same cross-section area and subjected under same tension.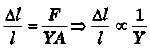
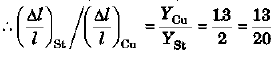
Ques 7: Calculate the approximate change in density of water in a lake at a depth of 400 m below the surface. The density of water at the surface is 1030 kg/m3 and bulk modulus of water is 2 × 109N/m2.
Sol:
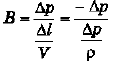
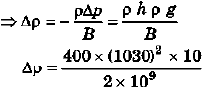
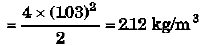
Ques 8: A wire of length 3 m, diameter 0.4 mm and Young's modulus 8 × 1010 N/m2 is suspended from a point and supports a heavy cylinder of volume 10-3 m3 at its lower end. Find the decrease in length when the metal cylinder is immersed in a liquid of density 800 kg/m3.
Sol: 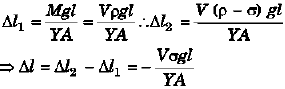
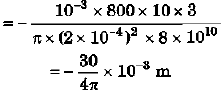
= -2.39 × 10-3 m
Ques 9: In taking a solid ball of rubber from the surface to the bottom of a lake of 180 m depth, reduction in the volume of the ball is 0.1%. The density of water of the lake is 1 × 103 kg/m . Determine the value of the bulk modulus of elasticity of rubber. (g = 9.8m/s2)
Sol: 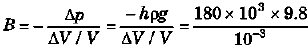
= 1.76 × 109 N/m2
Ques 10: A sphere of radius 10 cm and mass 25 kg is attached to the lower end of a steel wire of length 5 m and diameter 4 mm which is suspended from the ceiling of a room. The point of support is 521 cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position. (Ysteel =2 × 1011 N/m2)
Sol: 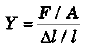
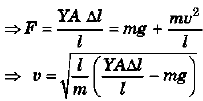
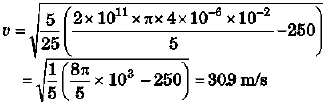
|
95 videos|367 docs|98 tests
|
FAQs on DC Pandey Solutions: Elasticity - Physics Class 11 - NEET
| 1. What is elasticity and why is it important in physics? |  |
| 2. How is elasticity measured and what are its units? |  |
| 3. What are some real-life applications of elasticity? |  |
| 4. How does temperature affect the elasticity of materials? |  |
| 5. Can elasticity be permanent? |  |

















