Ohm's Law & Drift of Electrons | Physics Class 12 - NEET PDF Download
| Table of contents |

|
| Electric Current in Conductors |

|
| What is Ohm's Law? |

|
| Drift of Electrons |

|
| Derivation of Expression of Drift Velocity |

|
| Mobility |

|
| Current Density |

|
| Solved Examples |

|
Think about everything you do in a day. From using your phone to turning on lights, electricity is what makes it all possible. But have you ever wondered how it all works? Well, it is all possible due to something called electric current.
In the first unit on 'Electrostatics', we studied the characteristics of charges at rest. However, most of the practical applications of electricity involve charges in motion. For instance, an electric bulb glows when charge flows through it, and an electric fan rotates when charges are made to pass through the coil.
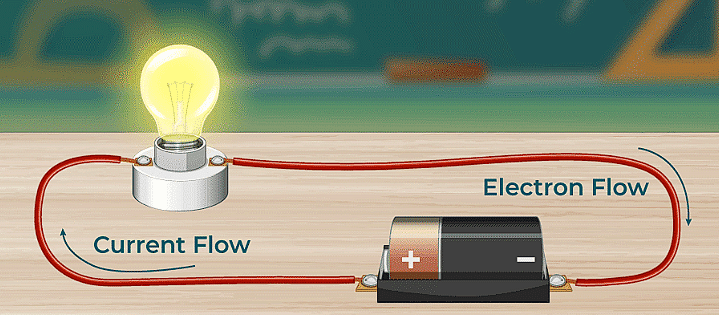 Electric Current
Electric Current
What is Electric Current?
Electric current is defined as the speed at which electrons move through a conductor, with its measurement unit being the Ampere in the International System of Units (SI).
Electrons are tiny constituents found within the molecular framework of matter. Their mobility varies depending on how tightly they are bound to the nucleus of an atom. When electrons are loosely bound, they have the freedom to move within the material. Since electrons carry a negative charge, their movement constitutes an electric current. The conductivity of a substance is determined by the extent to which electrons can move within it.
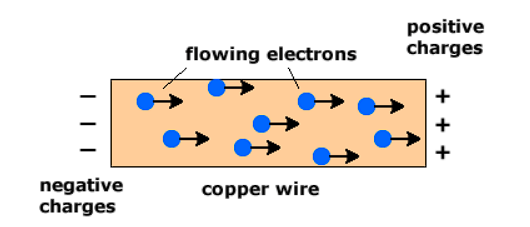
- Electric current is how fast electric charge moves through a material.
- For current to flow, there must be a net movement of charge across a surface. In an idle conductor, electrons move chaotically in all directions, and on average same number of electrons passes through each side of any imaginary surface, thus, canceling out any net charge across a surface.
- But when a conductor is connected to a battery, an electric field makes all free electrons move in a direction opposite to the electric field, creating a net flow of negative charge in a single direction.
- This is how electric current flows in a conductor.
If charge dq passes through an imaginary surface in time dt, then the current I through that surface is defined as I= dq/dt. This is the instantaneous current. The direction of the current is the direction of flow of positive charge carriers, or opposite to the flow of electrons.
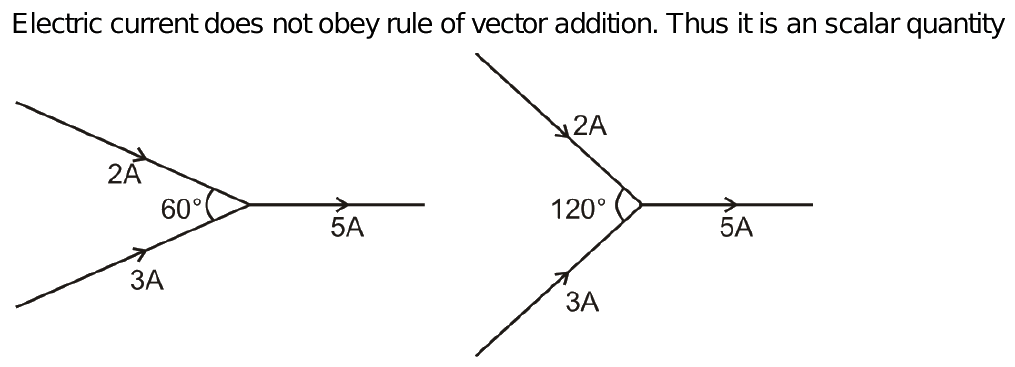
Current is a scalar quantity. Though electric current represents the direction of flow of positive charge, still, it is still treated as a scalar quantity. This is because electric current follows laws of scalar addition and not vector addition. The angle between the wires carrying electric current does not affect the total current in the circuit.
Unit of Electric Current
- The magnitude of electric current is measured in coulombs per second.
- The SI unit of electric current is Ampere and is denoted by the letter A.
- One Ampere is defined as one coulomb of charge moving past a point in one second. If 6.241 x 1018 electrons are flowing through our frame in one second then the electrical current flowing through it is ‘One Ampere.’
- The unit Ampere is widely used within electrical and electronic technology along with multipliers like milliamp (0.001A), microamp (0.000001A), and so forth.
Electric Current in Conductors
Conductors
Some things have electrons that aren't tightly held. These electrons can move easily and are called free electrons or conduction electrons. When in an electric field, they move against it. Materials with these electrons are called conductors.
- Examples include the human body, salty water, and metals like iron, silver, and gold. Silver is the best conductor of all metals.
 Conductors
Conductors
Insulators
Some things are called insulators. In these, electrons stick closely to atoms and there are no free electrons. When in an electric field, electrons may shift a bit but can't move far from their atoms. These materials are also called dielectrics.
 Insulators
Insulators
Semiconductors
Semiconductors act like insulators when their temperature is low, but as the temperature rises, a few electrons can break free and conduct electricity in response to an electric field.
- Their behavior isn't only influenced by temperature but also by doping, which introduces impurities to tweak their electrical properties.
- When an electron is freed in a semiconductor, it leaves a hole behind, and these holes also play a role in conducting electricity in semiconductors.
 Semiconductors
Semiconductors
Types of Electric Current
There are two types of electric currents: Alternating Current (AC) and Direct Current (DC).
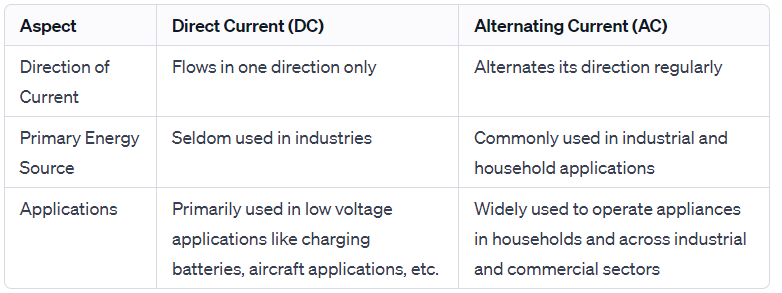
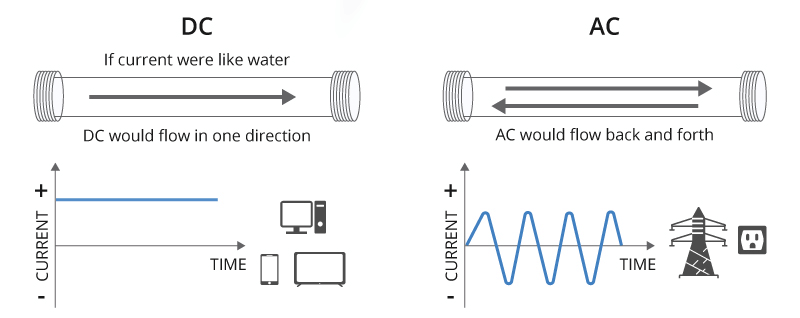 Representation of AC and DC Currents
Representation of AC and DC Currents
What is Ohm's Law?
Georg Simon Ohm, a German physicist, established the principle that the current passing through a wire is directly linked to the voltage difference across it.According to Ohm’s Law, the current flowing through a wire is directly proportional to the voltage applied at the ends of the wire provided that the temperature and conductivity remain the same.
V ∝ I
Upon removing the proportionality sign, a proportionality constant is introduced known as Resistance(R).
Where,
V is Voltage at the ends of conductor
R is Resistance offered by the conductor
I is Current through the wire
 Ohm's Law
Ohm's Law
Drift of Electrons
A conductor contains a large number of loosely bound electrons called free electrons or conduction electrons. These electrons move randomly in all directions within the entire volume of the conductor, and in this process keep on colliding with the atoms/molecules/ions of the conductor, changing their direction of motion at each collision.
When current is applied across the conductor the randomly moving electrons are subjected to electrical forces along the direction of the electric field.
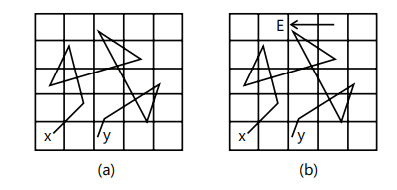 Motion of free electrons (a) in the absence of an electric field (b) in the presence of an electric fieldDue to this electric field, free electrons still have their random moving nature, but they will move through the conductor with a certain amount of force. The net velocity in a conductor due to the moving of electrons is referred to as the drift of electrons.
Motion of free electrons (a) in the absence of an electric field (b) in the presence of an electric fieldDue to this electric field, free electrons still have their random moving nature, but they will move through the conductor with a certain amount of force. The net velocity in a conductor due to the moving of electrons is referred to as the drift of electrons.
Derivation of Expression of Drift Velocity
When no electric field is applied across a conductor, the direction of motion of free electrons is so randomly distributed that the average thermal velocity of electrons is zero.
- There will be no net flow of electrons or charge in one particular direction in a metal conductor, hence no current.
- When some potential difference is applied across the two ends of a conductor, say a silver wire, an electric field is set up inside the conductor.
- The free electrons in a conductor experience a force in the direction opposite to that of the electric field.
- As a result of this, all of them are accelerated from the negative to the positive end of the conductor.
- On their way, the accelerated electrons suffer frequent collisions, against other silver atoms/ ions, and lose their kinetic energy.
- This happens in all successive collisions and the process continues till the electrons reach the positive end of the conductor.
- So each electron, in addition to its thermal velocity, acquires a velocity component in a direction opposite to the direction of the electric field due to acceleration given by the applied electric field.
At any given time, an electron has a velocity,
v1 = u1 + aτ1
where u1 is the thermal velocity of the electron, a is the acceleration caused by to electric field and τ1 is the time elapsed since it has suffered the last collision with an atom/ ion and is called relaxation time.
Similarly, the velocities of the other electrons are
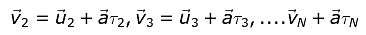
The average velocity of all the free electrons in the conductor is equal to the drift velocity vd of free electrons: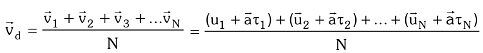
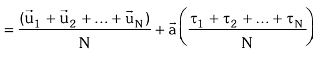
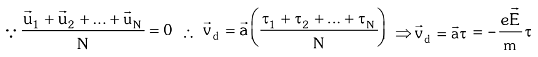
Here the first expression is taken as zero because it represents the average thermal velocity of the conductor which is always zero.
τ represents the average relaxation time. Its value is of the order of 10-14 seconds. The negative sign in the expression of drift velocity shows that its direction is always opposite to that of the applied electric field.
Relation between Drift Velocity and Electric Current
Let n = number density of free electrons and A = area of cross-section of the conductor
Number of free electrons in the conductor of length L = nAL,
The total charge on these free electrons Δq = neAvd
Time taken by drifting electrons to cross-conductor
Mobility
Conductivity arises from mobile charge carriers. In metals, these mobile charge carriers are electrons; in an ionized gas, they are electrons and positively charged ions; in an electrolyte, these can be both positive and negative ions.
- An important quantity is the mobility µ defined as the magnitude of the drift velocity of charge per unit electric field applied.
- Mathematically, µ = drift velocity / electric field =vd / E = (qEτ) / (mE) = qτ / m
- S.I. unit of mobility= m2s-1V-1
- From the expression, it is clear that the mobility of a charge carrier is inversely proportional to the mass of the charge carrier, so electrons being lighter than holes have very high mobility. This is the reason why they are considered the primary charge carriers in any circuit.
Current Density
Current density refers to the density of current flow in some conductors. It is denoted by the symbol J. Current Density and its measurement are very important as it is the measure of the flow of electric charge in amperes per unit area of cross-section i.e. m².
- Current Density formula can be expressed as, J= I/A
- This is a vector quantity because with the magnitude it has the direction of flow.
- Current is a macroscopic quantity and deals with the overall rate of flow of charge through a section. To specify the current with direction at the microscopic level at a point, the term current density is introduced. Current density at any point inside a conductor is defined as a vector having a magnitude equal to current per unit area surrounding that point. Remember area is normal to the direction of charge flow (or current passes) through that point.
- Current density at point P is given by:
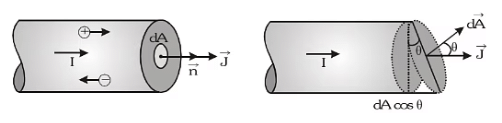
If the cross-sectional area is not normal to the current but makes an angle θ with the direction of the current
Current density is a vector quantity. Its direction is the same as that of Its S.I. unit is ampere/m2 and dimension [L–2A1].
Solved Examples
Q1. If the instantaneous current in a metallic wire is i=(5+10t)A then find the amount of charge flown through it from t=2s to t=3s.
Solution:
Given the instantaneous current,
Therefore, the current flowing through the wire from t=2s to t=3s is 60C - 30C = 30C
Q2. The figure below shows a plot of current I through the cross-section of a wire over a time interval of 10s. Find the amount of charge that flows through the wire during this period.
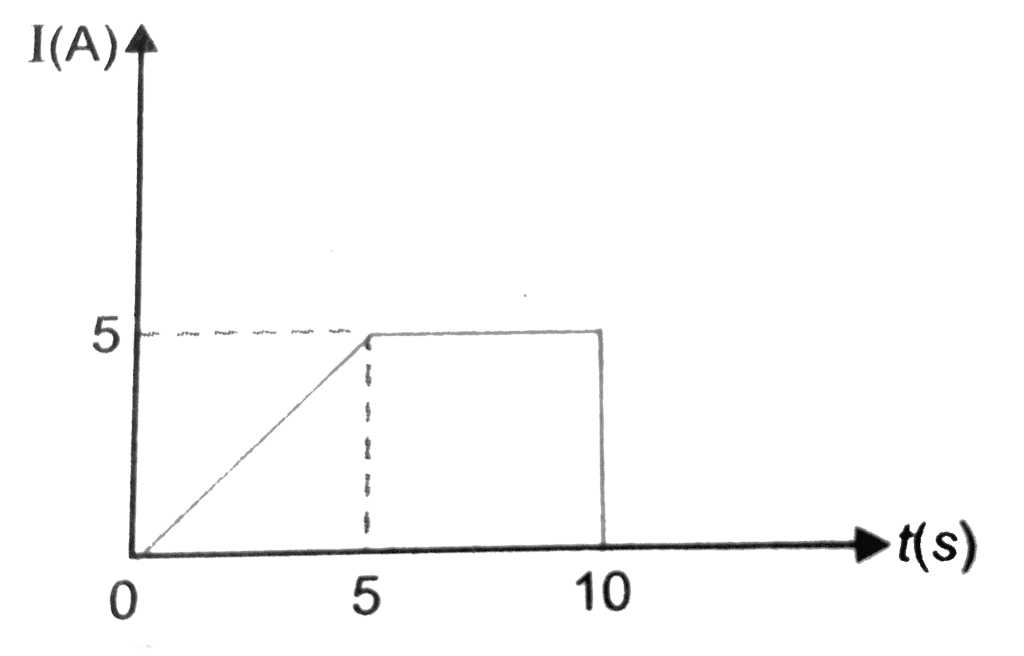
Solution:
Amount of Charge that flows in 10 seconds is = area under I - t graph
= area of triangle + area of sqaure
= (1/2 x base x height) + (side x side)
= (1/ 2 × 5 × 5) + (5× 5) = 12.5 + 25 = 37.5 C
Q3. If n =8.5 × 1028 m–3, how long does an electron take to drift from one end of a 3 m long wire to its other end? The area of the cross-section of the wire is 2.0 × 10-6 m2 and it carries a current of 3.0 Ampere. (JEE Mains 2019)
Solution:
For constant p.d. across the conductor, the electrons drift with constant drift velocity across it.
If we find the drift velocity, the time to drift across wire of constant length is easily found out
Given that:
(i) Number density n = 8.5 × 1028 m–3 (ii) Cross-sectional area A = 2.0 × 10-6m2
(iii) Current I = 3 A (iv) Charge on electron e = 1.6 × 10–19 C
Current in terms of drift speed is expressed as I = neAvd ⇒ vd = I/neA
Now time taken to cross the length ℓ of the wire is:
t= ℓ/vd = neAℓ/I = (8.5 × 1028x 1.6 × 10–19x 2.0 × 10-6 x 3) / 3 = 2.7 x 104 s
Q4. What is the drift velocity for the electrons in a conductor when an electric field of strength 200 V/m is applied to it and the mobility of electrons is 4.5 x 10-6 m2s-1V-1?
Solution:
Here, E= 200 V/m ; µ= 4.5 x 10-6 m2s-1V-1
Therefore, drift velocity, vd
vd = µE
= 4.5 x 10-6 x 200
= 9.0 x 10-4 m/s
Q5. A current of 5 A passes through a copper conductor (resistivity = 1.7×10 – 8Wm) of radius of cross-section 5 mm. Find the mobility of the charges if their drift velocity is 1.1×10 – 3 m/s.
(a)1.8m2/Vs (b)1.5 m2/Vs (c)1.3 m2/Vs (d) 1.0 m2/Vs
(JEE Mains, 2019)
Solution:
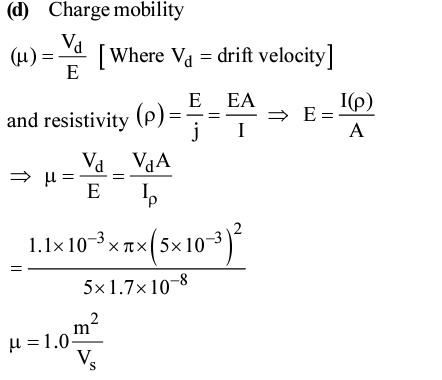
|
98 videos|334 docs|102 tests
|
FAQs on Ohm's Law & Drift of Electrons - Physics Class 12 - NEET
| 1. What is the definition of Ohm's Law and its mathematical expression? |  |
| 2. How does the drift of electrons contribute to electric current in conductors? |  |
| 3. What is the expression for drift velocity and how is it derived? |  |
| 4. What is the significance of mobility in the context of electric current? |  |
| 5. How is current density defined and what is its importance in electric current analysis? |  |























